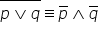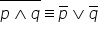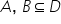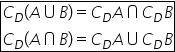Formule de calcul propozițional. Legile De Morgan

Maria nu are stilou Dar scrie frumos

să vedem cum putem să transcriem

această propoziție în limbaj matematic

dacă notăm propoziția Maria are

stilou cu p atunci propoziția Maria

nu are stilou la finante Haide

să notăm propoziția scrie frumos

cu q atunci această propoziție

Maria nu are stilou Dar scrie frumos

se poate citi și astfel Maria nu

are stilou și scrie frumos Deci

putem să punem o conjuncție între

propozițiile non pe și q un alt

exemplu dacă Maria câștigă concursul

și merge în excursie atunci ea

este fericită o să notăm cu propoziția

Maria câștigă concursul notez cu

q propoziția merge în excursie

și cu r propoziția Ea este fericită

observăm că între propozițiile

pe și q avem o conjuncție și de

asemenea regăsim sintagma dacă

atunci înseamnă că avem o implicație

deci putem să scriem astfel propoziția

p și q implică aer aceste formule

pe care le am găsit non p și q

respectiv p și q implică aer se

numesc formulă de calcul prepozițional

și despre acestea vreau să discutăm

în filmul acesta formulele de calcul

prepozițional se notează de obicei

cu litere grecești Alfa Beta gamă

și așa mai departe iar literele

p q r care apar în cadrul acestora

se numesc variabile propoziționale

formulele propoziționale se pot

nota și scriind în paranteză variabilele

care apar deci putem să scriem

Alfa și în paranteză pe și q respectiv

Beta și în paranteză să scrie în

propozițiile p q r care apar în

cadrul acestei formule prin urmare

o formulă prepozițională este o

expresie obținută din propoziții

simple cu ajutorul operatorilor

logici două formule Alfa și Beta

se numesc echivalente și o să scrie

astfel dacă pentru orice valori

de adevăr ale variabilelor propoziționale

expresiile au aceeași valoare de

adevăr o să vedem imediat câteva

exemple de formule echivalente

Dar mai întâi Aș vrea să facem

o scurtă recapitulare a operațiilor

cu propoziții pe care le am văzut

în lecțiile trecute operațiile

pe care le am învățat în acest

capitol au fost negația conjunctia

disjuncția implicația și echivalența

aceste simboluri se mai numesc

și operatori logici negația se

poate înota așa sau se mai Notează

și cu o bară deasupra Deci notații

anunte scrisă așa este același

lucru cu unp barat sau Notați aceasta

nu n p și q înseamnă același lucru

cu p și q barat conține cont de

ordinea în care am scris acești

operatori pentru că aceasta este

și regula de prioritate a operațiilor

între o formulă propozițională

ești mai întâi o să facem negația

apoi conjuncția disjuncția implicația

și echivalența în cazul în care

între o formulă apar și paranteze

o să ținem cont și de acestea și

acum să dăm un exemplu de două

formule echivalente de exemplu

negația propoziției P sau q este

logic echivalentă cu non p și q

și o să demonstrăm imediat această

relație o altă relație de echivalență

negația propoziției pe și q este

logic echivalentă cu negația propoziției

pe sau negația propoziției q vom

demonstra mai întâi prima relație

pentru aceasta îmi face un tabel

pentru valorile de adevăr avem

propoziția pe propoziția q propoziția

P sau Q urmează negația propoziție

P sau Q pe care am notat o o Alfa

în continuare avem negația propoziției

pe negația propoziției q și conjuncția

dintre cele două negații iar această

formulă a notat o cu Beta ne propunem

Să arătăm că Alfa este echivalentă

cu Beta pe primele două coloane

vom scrie valorile de adevăr pentru

propozitiile p și q 0 0 1 1 0 1

0 1 în cazul în care sunt două

propoziții în raport mula avem

2 la a doua combinații posibile

adică patru iar dacă sunt trei

propoziții pe q r avem 2 la a treia

combinații posibile adică 8 Acum

ne propunem să scriem valoarea

de adevăr pentru propoziția pe

sau Q mare amintească disjuncția

este adevărată dacă cel puțin una

dintre cele două propoziții este

adevărată enorm are o să avem 0

1 1 1 acum urmează negația aceste

propoziții 1 0 0 0 în continuare

o să scriem negația propoziției

pe Deci ne uităm pe prima coloană

dacă este falsă negația este adevărată

și dacă p este adevărată a acesteia

este falsă urmează negația propoziției

q ne uităm pe această coloană și

avem 1 0 1 0 conjuncția dintre

aceste două propoziții conjuncția

este adevărată dacă ambele propoziții

sunt adevărate în caz contrar este

falsă Deci o să avem 1 0 0 0 acum

dacă ne uităm în aceste coloane

în care avem formulele Alfa și

Beta observăm că ele au aceleași

valori de adevăr prin urmare ma

spune că cele două formule sunt

echivalente în continuare ne propunem

să demonstrăm a doua relație de

echivalența pentru aceasta vom

face un alt tabel avem propoziția

p q p și q formează negația propoziție

pe și q pe care o să o notăm cu

Alpha nunte nunțiu și disjuncția

propozițiilor p q pe care am notată

cu Beta să verificăm dacă Alfa

Este logic echivalentă cu Beta

scrie Dino valorile de adevăr pentru

p și q 0 0 1 1 0 1 0 1 p și q este

adevărată dacă Ambele sunt adevărate

în caz contrar este falsă negația

propoziției pe și q 1 1 1 0 1 iază

Nan pe nici nu uităm pe prima coloană

și scrie negația aceste propoziții

avem 11.00 urmează non Q10 1 0

și acum facem disjuncția dintre

aceste două propoziții dezumflam

este adevărată dacă cel puțin una

dintre propoziții este adevărată

prin urmare o să avem 1 1 1 0 dacă

ne uităm la valorile de adevăr

pentru formulele Alfa și Beta observăm

că acestea au aceeași valoare de

adevăr prin urmare Alfa este echivalentă

cu Beta aceste două relații pe

care tocmai am demonstrat se numesc

formulele lui de Morgan sau legile

lui de Morgan să reținem Așadar

aceste două legi ale lui de Morgan

și să vedem acum concret Cum putem

să le dacă avem următoarea propoziție

triunghiul este isoscel sau echilateral

și dorim să scriem negația aceste

propoziții o să folosim prima formulăm

având în vedere că avem aici o

disjuncție negația disjuncția Este

logic echivalentă cu conjuncția

negațiilor celor două propoziții

prin urmare trebuie să negăm propoziția

triunghiul este isoscel am folosit

aici această negație negăm și a

doua propoziție triunghiul nu este

echilateral iar disjuncția se transformă

în conjuncție și atunci negați

aceste propoziții suna astfel triunghiul

nu este isoscel și nu este echilateral

un alt exemplu avem următoarea

propoziție triunghiul este isoscel

și are un unghi drept observăm

că avem aici o conjuncție prin

urmare trebuie Să aplicăm 2-a formulăm

negația unei conjuncții este echivalentă

cu disjuncția negațiilor Așadar

negăm cele două propoziții negația

primei propoziții va fi triunghiul

nu este isoscel negația Propoziție

are un unghi drept este propoziția

nu are un unghi drept iar cuvântul

și devine sau și atunci te Garcia

va fi următoarea propoziție triunghiul

nu este isoscel sau nu are un unghi

drept acestea sunt legile lui de

Morgan pentru calculul propozițiilor

însă aceste două formule pot fi

aplicate și în cazul în care avem

operații cu mulțimi vă reamintesc

că fiecare operație cu propoziții

a fost asociată cu o operație cu

mulțimi dacă vă mai amintiți negația

a fost asociată cu complementară

unei mulțimi disjuncte a fost asociată

cu Reuniunea mulțimilor și conjuncția

a fost asociată cu intersecția

mulțimilor în mare Haide să vedem

cum putem să transcriem aceste

formule folosind operații cu mulțimi

Fie a și b două submulțimi ale

unei mulțimi de atunci disjuncția

propozițiilor p și q poate fi asociată

cu Reuniunea celor două mulțimi

de ce avem A reunit cu b însă aici

avem negația disjuncție y prin

urmare trebuie să aplicăm complementara

acestei mulțimi în raport cu d

egal mai departe Nan pe poate fi

asociată cu complementara mulțimii

A în raport cu d conjuncția înseamnă

intersecție de mulțimi iar negația

propoziției q este asociată cu

complementara mulțimii B în raport

cu d și atunci această relație

se citește astfel complementara

reuniunii a doua mulțimi este egală

cu intersecția complementarelor

să vedem acum cum putem să transcriem

a doua formulă folosind operații

cu mulțimi avem aici o conjuncție

de propoziții conjuncția si transcrie

ca intersecție de mulțimi A intersectată

cu b avem și aici negația conjuncție

prin urmare o să avem complementară

acestei mulțimi în raport cu d

egal negația lui Perry este asociată

cu complementarea mulțimii A în

raport cu d iar disjuncția propozițiilor

înseamnă de fapt reuniune de mulțimi

reunită cu complementara mulțimii

B în raport cu d citim astfel complementarea

intersecției a două mulțimi este

egală cu Reuniunea complementarelor

acestea sunt formulele lui de Morgan

în cazul operațiilor cu mulțimi

iar în continuare o să facem câteva

exerciții în care o să stabilim

valorile de adevăr ale unor formule

propoziționale avem următoarea

formulă prepozițională pe care

am notat tu cu gama pe implica

q sau Q implica Pentru a stabili

valorile de adevăr pentru formula

gama am realizat un tabel în care

vom trece valorile de adevăr posibile

pentru propozițiile pe și q avem

0 0 1 1 0 1 0 1 moment ce avem

aici paranteze romsine cont de

acestea prin urmare mai trebuie

să trecem în tabel implicația pe

implică q apoi cu implică pe iar

ultima coloană avem disjuncția

dintre cele 2 implicații mai exact

formula Gama să stabilim acum valoarea

de adevăr pentru propoziția pe

implică q aceasta este falsă numai

în condițiile în care p este adevărată

și q este falsă deci pe această

linie avem zero în rest peste tot

o să avem unul implică pe este

falsă dacă q este adevărată și

pe este falsă aici avem zero în

rest peste tot unul în continuare

trebuie să facem disjuncția dintre

aceste două propoziții aceasta

este adevărată dacă cel puțin una

dintre propoziții este adevărată

o să avem 1 1 1 1 observăm că formula

gama are numai valoarea 1 indiferent

de valorile de adevăr ale propozițiilor

p și q o astfel de expresie se

numește tautologie să reținem deci

că o tautologie este o expresie

adevărată indiferent de valorile

de adevăr ale variabilelor propoziționale

Eu zic că sunt distractive aceste

exerciții Ce ziceți Mai facem unul

am auzit un da colectiv așa pot

să mai fac un exercițiu avem următoarea

formulă prepozițională pe care

am notat o cu Delta pe implică

q sau pe echivalent cu q și p după

cum observăm în această formulă

nu avem paranteze dar trebuie să

ținem cont de ordinea în care aplicăm

operatorii logici avem o implicație

și o disjuncție prioritară va fi

disjuncția dacă doriți putem să

punem o paranteză ca să fie mai

clar acest lucru apoi avem o echivalență

și o conjuncție prioritară va fi

conjuncția acum între implicație

și echivalență prioritară este

implicația deci putem să punem

aici o paranteză dreaptă trece

mai întâi valorile de adevăr pentru

p și q urmează q sau pe adică această

paranteză rotundă după aceea am

scris paranteza dreaptă pe implică

q sau pe după aceea o să scrie

în valoarea de adevăr pentru această

paranteză rotundă q și P și la

final echivalența dintre cele două

paranteze adică formula Deltă 0

0 1 1 0 1 0 1 q sau p este adevărată

dacă cel puțin una dintre propoziții

este adevărată 0 1 1 1 pe implică

q sau pe ne uităm pe această coloană

și pe coloana cu propoziția q sau

pe trebuie să scrie valoarea de

adevăr pentru implicația a acestora

implicația este falsă Dacă prima

propoziție este adevărată și a

doua propoziție este falsă însă

nu avem această situație aici prin

urmare această implicație va fi

adevărată acum să scrii în valoarea

de adevăr pentru propoziția q și

p conjuncția este adevărată dacă

ambele propoziții sunt adevărate

ne uităm pe primele două coloane

observăm că în ultimul caz avem

o conjuncție adevărată în rest

este falsă Și acum trebuie să stabilim

valoarea de adevăr pentru echivalența

dintre aceste două propoziții echivalența

este adevărată numai atunci când

cele două propoziții au aceeași

valoare de adevăr adică aici în

rest avem peste tot zero acestea

au fost exercițiile cu formule

de calcul propozițional vă rămâne

ca temă să arătați că negația propoziției

nu pe Este logic echivalentă cu

propoziția pe adică dubla negație

a unei propoziții coincide cu propoziția

inițială și mai putem să arătați

că propoziția pe sau Nan pe este

o tautologie o scurtă observație

aș vrea să mai facem această lege

a dublei negații nu se aplică întotdeauna

și în gramatica limbii române de

exemplu dacă avem propoziția nu

am nicio problemă aici avem o dubla

negație dacă tăiem aceste negații

rămâne în propoziția Am o problemă

însă propoziția nu am nicio problemă

Nu este același lucru cu propoziția

Am o problemă prin urmare putem

trage concluzia că gramatica nu

are logică dar nu are matematica

are logică din moment ce este adevărată

propoziția Dacă 1 plus 1 egal 5

atunci elefantul zboară