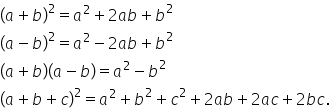Formule pt. calcul prescurtat
Tag-uri
Partajeaza in Google Classroom

Transcript
formule de calcul prescurtat în
calcule cu numere reale reprezentate
prin litere vom întâlni adesea
pătratul unei sume de doi termeni
sau pătratul diferenței a două
numere reale ne propunem să găsim
o formulă Generală de calcul pentru
pătratul sumei a doi termeni respectiv
pentru pătratul diferenței pe care
să o putem aplica în exercițiile
următoare să deducem mai întâi
o formula de calcul pentru pătratul
unei sume Fie a și b două numere
reale și vrem să găsim o formulă
de calcul pentru a plus b la a
doua conform definiției puterii
a plus b la a doua este egal cu
a plus b pe lângă a plus b acum
asa desfacem paranteza înmulțim
numărul a cu fiecare număr din
a doua paranteză apoi numărul b
cu fiecare termen din a doua paranteză
și obținem a ori a plus a ori b
plus de ori a plus b ori b a ori
a este a la a doua plus ab plus
în loc de Ba Putem să scriem ab
pentru că înmulțirea este comutativă
plus de la a doua avem termeni
asemenea a b plus a b și obținem
a la a doua plus 2 ab plus b la
a doua să vedem și care va fi formula
pentru pătratul diferenței a două
numere reale a minus b totul la
a doua este a minus b pe lângă
a minus b procedăm ca și în cazul
anterior desfacem parantezele și
avem a ori a plus a ori a minus
b a minus b ori a minus b ori minus
b penal Ana a doua a ori minus
b este minus abe aici inversăm
locul factorilor și scrie minus
ab iar minus b ori minus b va fi
plus b la a doua egal avem termenii
asemenea minus a b minus ab are
va fi minus 2ab descrie a pătrat
minus 2ab plus de la a doua aceasta
va fi formula Generală de calcul
pentru pătratul diferenței a două
numere reale să deducem și eu o
formulă pentru produsul dintre
suma și diferența a doi termeni
a plus b pe lângă a minus b la
fie egal cu a ori a plus a ori
minus b plus b ori a plus b ori
a minus b egal cu ala a doua minus
a b plus a b a minus b la a doua
minus a b și plus a b se reduc
și obținem în final a la a doua
minus b la a doua și mai putem
întâlni în calcule și pătratul
sumei a trei numere reale a plus
b plus c totul la a doua va fi
egal cu a plus b plus c pe lângă
a plus b plus c se desfac în mod
Analog parantezele Înmulțind primul
număr din paranteză cu fiecare
număr din a doua paranteză și așa
mai departe după ce se vor face
toate calculele se va ajunge la
formula a la a doua plus b la a
doua plus c la a doua plus 2 ab
plus 2 ace plus 2 b c acestea sunt
formulele de calcul prescurtat
pe care le vom folosi în exercițiile
următoare le mai repetăm odată
a plus b la a doua este egal cu
a la a doua plus doi a b plus b
la a doua a minus b totul la a
doua este egal cu a la a doua minus
2ab plus b la a doua a plus b pe
lângă a minus b vă fie a la a doua
minus de la a doua și a plus b
plus c totul la a doua este egal
cu a la a doua plus b la a doua
plus c la a doua plus doi a b plus
2 AC plus 2 b c și acum să revenim
la exercițiile inițiale pe care
mi le am propus x plus 3 la a doua
nu folosi prima formulă pătratul
unei sume în loc de a în exercițiu
avem x și în loc de beof m3m obține
x pătrat plus doi ori x ori 3 plus
3 la a doua egal mai departe cu
x la a doua plus 6x plus 9 și x
minus 3 la a doua minus folosi
a doua formulă de calcul prescurtat
este x la a doua minus 2 ori x
ori 3 plus 3 la a doua egal mai
departe cu x la a doua minus 6x
plus 9 în continuare o să facem
câteva exerciții în care o să aplicăm
aceste formule primul exercițiu
2x plus 1 la a doua nu folosi prima
formulă în loc de ei avem 2x și
în loc de beof M1 Așadar vom avea
2 x totul la a doua plus doi ori
doi x ori 1 plus 1 la a doua egal
trebuie să ridicăm la a doua fiecare
Factor din paranteză 2 la a doua
este 4 x pătrat plus 4x plus 1
2 3x minus 2y totul la pătrat avem
pătratul diferenței a două numere
reale evidență folosi a doua formulă
în loc de ei avem 3x și în loc
de beof m2 Y5 vom obține 3 x la
pătrat minus 2 ori 3 x ori 2 y
plus 2y la pătrat egal cu 9 x la
a doua minus 2 ori 3 6 ori 2 12
x y plus 4 y la a doua următorul
exercițiu radical din 5 plus 2
totul la a doua va fi egal cu radical
din 5 la a doua plus 2 ori radical
din 5 ori 2 plus 2 la a doua egal
orice radical ridicat la puterea
a doua a ne va fi acel număr de
sub radical pentru că extragerea
rădăcinii pătrate și ridicarea
la puterea a doua a sunt operații
inverse care se anulează reciproc
plus 4 radical din 5 plus patru
putem să mai adunăm și 5 cu 4 și
obținem 9 plus 4 radical din 5
4 1 minus radical din 3 totul la
a doua folosind formula pentru
pătratul diferenței a doi termeni
și obținem 1 la a doua minus doi
ori unu ori radical din 3 plus
radical din 3 la a doua egal mai
departe cu 1 minus 2 radical din
3 plus 3 adunăm unu plus trei și
obținem 4 minus 2 radical din 3
5 2x plus radical din 7 totul la
a doua va fi egal cu 2x la a doua
plus 2 ori 2 x ori radical din
7 plus radical din 7 la a doua
egal cu patru x pătrat plus aici
o să scriem toți cu eficienți în
fața literei x și scriem 4 radical
din 7 x plus 7 6 x minus radical
din 3 supra 2 totul la puterea
a doua va fi egal cu x la a doua
minus 2 ori x ori radical din 3
supra 2 plus radical din 3 supra
2 la a doua egal mai departe cu
x la a doua minus aici putem să
simplificăm pe diagonală cu 2 și
rămâne x radical din 3 plus 3 supra
4 următorul exercițiu 7 a minus
5 pe lângă a plus 5 aici vom folosi
3-a formulă de calcul prescurtat
produsul dintre suma și diferența
a două numere reale și va fi egal
cu a la a doua minus 5 la a doua
egal mai departe cu a la a doua
minus 25 8 radical din 5 plus radical
din 3 pe lângă radical din 5 minus
radical din 3 va fi egal cu radical
din 5 la a doua minus radical din
3 la a doua egal mai departe cu
5 minus 3 egal cu 2 9 x la a doua
plus x plus 1 totul la a doua observăm
că avem pătratul unei sume de trei
numere reale Așadar folosim ultima
formulă de calcul prescurtat se
ridică la a doua fiecare număr
din paranteză nu mai avea x la
a doua totul la a doua plus x la
a doua plus 1 la a doua plus doi
ori x la a doua ori x plus doi
ori x ori unu plus doi ori x la
a doua ori 1 penal cu x la a patra
plus x la a doua plus 1 plus 2x
la a doua ori x este x la a treia
plus 2x plus 2x la a doua egal
termenii asemenea sunt x la a doua
și 2x la a doua ați termeni asemenea
nu mai avem x la a patra plus x
la a doua plus 2x la a doua este
3x la a doua plus 1 plus 2x la
a treia plus 2x o să le aranjăm
termenii ca să scriem în ordinea
descrescătoare a puterilor lui
x și obținem x la a patra plus
2x la a treia plus 3x la a doua
plus 2x plus 1 și ultimul exercițiu
4x minus 3 totul la a doua plus
3x plus 2 la a doua minus 5x plus
2 pe lângă 5x minus 2 observăm
că în acest exercițiu va trebui
să aplicăm primele trei formule
de calcul prescurtat pentru că
avem și pătratul diferenței și
pătratul sumei a două numere reale
respectiv produsul dintre suma
și diferența a două numere reale
4x minus 3 totul la a doua va fi
egal cu 4 x la a doua minus 2 ori
4 x ori 3 plus 3 la a doua apoi
3x plus 2 la a doua va fi egal
cu 3X la a doua plus 2 ori 3 x
ori 2 plus 2 la a doua minus 5x
plus 2 pe lângă 5x minus 2 va fi
egal cu 5 și x la a doua minus
2 la a doua penal cu 16 x pătrat
minus 2 ori 4 este 8 8 ori 3 24
x plus 9 plus 9 x pătrat plus 2
ori 3 6 ori 212 x plus 4 minus
5 x la a doua este 25 x la a doua
minus 4 am păstrat paranteza fiindcă
avem minus în fața acestei ei și
va trebui să schimbăm semnele final
până la paranteză să încercăm să
adunăm termenii asemenea avem 16
x pătrat cu 9 x pătrat este egal
cu 25 x pătrat apoi mai avem minus
24 x plus 12 x este egal cu minus
12x iar 9 plus patru este 13 minus
acum desfacem paranteza schimbând
semnele 25 x la a doua plus 4 egal
termenii asemenea sunt 25 x pătrat
Minus 25 x pătrat Aceștia se reduc
mai rămâne minus 12x și 13 plus
patru este egal cu 17