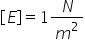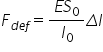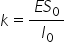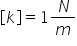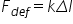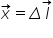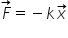Forţa elastică. Legea Hooke.
Tag-uri
Partajeaza in Google Classroom

Transcript
în cea de a șaptea lecție de mecanicul
Antonia Ana vom discuta despre
fenomenul de la esti citate și
despre legea Cu ce elasticitate
este proprietatea unor corpuri
dar a venit de la sine la forma
și dimensiunile inițiale după ce
încetează acțiunea forțelor exterioare
care le au deformat proprietatea
sau fenomenul opus celui de elasticitate
se numește plasticitate și reprezintă
incapacitatea corpului de a reveni
la forma inițială După ce a fost
de formă îmi plac tecum elasticitatea
este limitată întotdeauna adică
există o deformare maximă a corpurilor
elastici peste care aceștia își
pierd proprietatea de a fi elastici
și devin plastici nume revin la
forma inițială Se poate stabili
în experimental o relație între
forța deformatoare a unui corp
și alungirea corpului respectiv
datorită acestei forțe mai exact
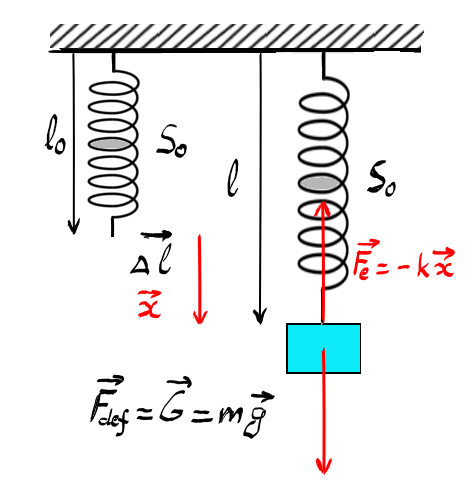
se ia pe Exemplu un Resort Care
este fixat la un cap și avem de
tort de solul acesta care este
sub acțiunea se află sub acțiunea
unei forțe deformatoare la celălalt
capăt dacă notăm cu L 0 lungimea
deformată a resortului și cu Delta
l alungirea resortului datorat
forței putem măsura pentru verii
valori ale forței deformatoare
de a lungimea alungirea resortului
de el tighel obținem că alungirea
Delta l e proporțională cu forța
deformatoare râde de ce avem o
relație de felul acesta pentru
moment ne referim doar la magnitudinea
sau modulul forței deformatoare
și nu la Direcția și sensul acestui
Factor Deci Delta l în această
relație este alungirea resortului
fiind egală cu lungimea finală
minus lungimea inițială ne deformată
și ies de după cum am spus este
forța deformatoare k k este constanta
elastică și se măsoară în Newton
pe metru de ce unitate de măsură
pentru Constanța de elastică este
Newton pe metru pentru a introduce
forța elastică Care este forța
ce se dezvoltă în Resort și care
se opune forței deformatoare încercând
să aducă resortul în stare deformată
de chin acest caz forța elastică
va avea sensul opus forței deformatoare
de ce acesta este f n forță elastică
care încearcă să aducă resortul
în starea țeava pentru a defini
această forță elastică definim
vectorul de formare vectorul de
formare se notează cu x este un
factor și are magnitudinea sau
modulul egal cu alungirea Delta
l Iar semnul sau sensul lui este
pozitiv Deci sensul este mai mare
decât 0 în cazul alungirii și mai
mic decât 0 alungire și mai mic
decât 0 pentru o deformare a resortului
în care Evident axa o x considerată
are sensul forței deformatoare
de ce Aceasta este o x și vectorul
de formare are sens pozitiv în
cazul alungirii și sens negativ
în cazul comprimării resortului
modulul lui fiind întotdeauna Delta
l cu acestea se poate defini forța
elastică notată cu f e ca un Vector
Care este egal cu este forța deformatoare
are aceeași direcție dar sens contrar
și care este egal cu minus Constanta
elastică înmulțită cu vectorul
de formare x Definiți după cum
e sus mai sus care are din nou
sens pozitiv în cazul alungirii
și sens negativ sau semn negativ
însă în cazul deformării în cazul
general însă forța deformatoare
nu acționează într un punct ce
mai degrabă pe o suprafață a corpului
supus deformării de aceea este
mai util să introducem forța deformatoare
pe unitatea de suprafață a corpului
Ce este de format această cantitate
această mărime se numește furtuni
tari se notează cu Sigma de asemeni
introducem noțiunea de deformare
relativă Care este alungirea sau
de formare a totală a corpului
împărțită la dimensiunea inițială
nedeformata a corpului care se
notează cu epsilon la fel experimental
se stabilește așa numita lege cu
cookson de fizicianul are a demonstrat
experimental care spune că efortul
unitar este direct proporțional
cu deformarea relativ o formulare
echivalentă acestei legi este următoarea
Delta lp0 adică ypsilon este egal
cu 1 pe înmulțit cu F supra 0 adică
efortul unitar Constanța de proporționalitate
m se numește modulul Young ținând
cont de relația pentru forța elastică
Care este f este egal cu modulul
modulul forței elastice este egal
cu un CAR or Delta l Se poate stabili
imediat relația dintre modulul
Ianc și Constanta de Constanța
elastică k Ea este aceasta modulul
lui Young se măsoară în newtoni
pe metru pătrat și este o constantă
de materie Care corp are o în modul
Young al său există și o anumită
limită de proporționalitate limita
de proporționalitate este deformarea
maximă a unui corp pentru care
legile despre calendar cu tot mai
exact legea Hook și legea forței
elastice sunt corecte asta înseamnă
că în practică pentru orice corp
elastic se stabilește experimental
o anumită curbă Sigma epsilon sau
curbă efort unitară deformare relativă
care are tipic o formă de salut
următor are o porțiune în care
crește liniar nu este foarte liniar
în desenul meu de imaginație mă
că Viva imaginație văd că este
liniarul până la un anumit punct
a apoi apare încă o zonă în care
de formare a continuă dar nu este
liniară până la un punct b apoi
este o vine în platoul în care
fără de fără efortul unitar crește
foarte puțin și fluctuează iar
apoi apare un punct d în care corpul
se rupe Deci corpurile elastici
vin cu o așa numită curbă efortul
unitar deformare relativă care
tip plic au aceste trei zone trei
regiuni zona de proporționalitate
în de la zero de la originea axelor
până la un anumit punct a unde
Sigma este proporțional cu epsilon
apoi o zonă o b care zona de la
stie citate între punctele a și
b corpul își păstrează proprietatea
de elasticitate Adică o dată forța
oprită și revine la forma inițială
numai că dependența dintre Sigma
și epsilon între a și b nu mai
este liniară apoi între b și d
avem o zonă de plasticitate corpul
nu își mai revine la forma inițială
și în final punct la punctul de
apare ruperea corpului tensiunea
din fir este forța elastică ce
întinde un fir și ea acționează
În toate punctele ce se află dea
lungul firului pentru a explica
această în acest tip particular
de forță elastică Să considerăm
un corp Ce este atârnat cu ajutorul
unui fir elastic de un tavan de
ce avem acest corp atârnat de tavan
cu ajutorul unui fir corpul are
greutatea G care acționează ca
o forță deformatoare asupra firului
în punctul A în care corpul este
atașat va apara o forță elastică
pe care o notăm cu d 1 care are
sens opus greutăți de asemeni în
punctul B în care firul este atașat
de tavan apare o altă forță elastică
de 2 datorită întinderii firului
în această forță elastică încercând
să readucă firul la dimensiunea
originală căruia îi răspunde o
acțiune din partea ta Vali notată
cu forță de asemenea în orice punct
luăm un punct la întâmplare ce
de a lungul firului în orice punct
apare o pereche de forțe elastice
notate cu D3 și D4 care acționează
pentru readucerea firului elastic
la lungimea inițială în fiecare
din aceste puncte Putem să scriem
cea de a doua si dat cerea treia
lege a dinamicii și anume că acțiunea
este egală cu reacțiunea mai concret
în a putem Scrie câte unul este
egal cu minus greutatea vectorial
bineînțeles în punctul B putem
scrie că te 2 este egal cu minus
r iar îmi Punctul C care lino este
un punct luate la întâmplare dealungul
fiului putem scrie că cele două
tensiuni sunt egale și de sens
contrar în cazul particular în
care masa fierului este neglijabilă
nici musafirului poate fi aproximată
cu zero ceea ce este în încerci
este de obicei adevărat pentru
că firele au mase mult mai mici
decât corpurile cu care sunt folosite
în acest caz putem scrie că toate
aceste tensiuni sunt egale în modulul
lor magneți identici de 2 t 1 este
egal cu T2 Care este egal cu 3
care este egal cu T4 și așa mai
departe Toate aceste forțe lactice
din fier numită tensiuni Da lungul
șirului sunt egali ceea ce simplifică
problema

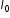 și aria secțiunii transversale
și aria secțiunii transversale 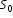 .
.
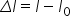
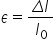 .
.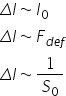
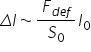
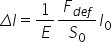
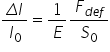
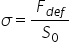
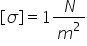
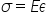 .
.