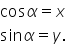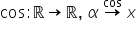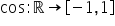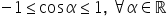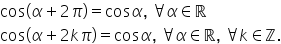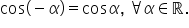Funcția cosinus

în această lecție o să discutăm

despre funcția cosinus și proprietățile

acesteia avem în imagine un cerc

trigonometric și am construit un

unghi Alfa căruia îi corespunde

pe cerc punctul M o m este rază

În cercul trigonometric prin urmare

lungimea acestuia este egală cu

1 dacă proiectăm raza om pe cele

două axa o x respectiv o igrec

obținem abscisa și ordonata punctului

m Dacă ne uităm în acest triunghi

dreptunghic cosinus de Alfa este

raportul dintre cateta alăturată

adică acest segment roz și ipotenuza

om însă om este egal cu 1 m Prin

urmare avem cos de Alfa egal cu

x observăm Așadar că putem să construim

o funcție care Asociază fiecărui

unghi Alfa abscisa punctului corespunzător

de pe cerc iar această funcție

va fi funcția cosinus încet trigonometric

putem avea atât unghiuri pozitive

cât și negative prin urmare domeniul

de definiție a funcției cosinus

va fi mulțimea numerelor reale

și acum Haideți să vedem semnul

aceste funcții pentru unghiuri

în cele patru cadrane dacă asta

este un unghi în cadranul întâi

atunci funcția cosinus este pozitivă

observăm că abscisa acestui punct

este pozitivă deoarece suntem la

dreapta axei o x y dacă unghiul

Alfa este în cadranul 3 Deci Alfa

aparține intervalului pi 3 pi supra

2 funcția cosinus este de asemenea

negativă Iată și în acest caz x

este negativ iar dacă unghiul este

în cadranul al patrulea Deci unghiul

Alfa este în intervalul 3 pi pe

2 2 pi atunci funcția cosinus este

pozitivă să reținem Așadar că funcția

cosinus ia valori pozitive în cadranul

1 și 4 și valori negative în cadranul

2 și 3 să vedem în continuare imaginea

acestei funcții cu alte cuvinte

Vrem să vedem Care este cea mai

mică respectiv cea mai mare valoare

pe care o poate lua funcția cosinus

dacă unghiul Alfa are 0 Radian

sau 0 grade atunci cosinus de 0

este egal cu 1 observăm că abscisa

acestui punct este 1 pentru că

o m este rază dacă unghiul Alfa

are pi supra 2 radiani atunci abscisa

punctului va fi 0 Deci cosinus

de pi pe 2 este 0 dacă Alfa are

măsura de radiani adică 180 de

grade atunci cosinus de pi este

minus 1 iar dacă Alfa este 3pi

pe 2 cosinus de 3pi pe 2 va fi

0 în cazul în care Alfa are măsura

egală cu doi pira Deian atunci

cosinus de 2 pi este egal cu unu

observăm Așadar că cea mai mică

valoare pe care o poate lua funcția

cosinus este minus unu pentru unghiul

cu măsura de pira Dihanie și cea

mai mare valoare pe care o poate

lua este 1 pentru 0 respectiv 2

pi radiani astfel putem trage concluzia

că imaginea funcției cosinus este

intervalul închis minus unu unu

și acum să discutăm câteva aspecte

legate de monotonia funcției dacă

unghiul Alfa este un unghi în cadranul

întâi atunci funcția cosinus este

descrescătoare ne uităm la segmentului

roz și observăm că Pe măsură ce

unghiul Alfa crește abscisa punctului

scade Așadar funcția cosinus este

descrescătoare pentru unghiurile

din primul tabel n Dacă Alfa este

un unghi cadranul al doilea funcția

cosinus este de asemenea descrescătoare

pentru că aici avem valori negative

Putem verifica monotonia funcției

și uitând Nela abscisele acestor

puncte Deci funcția cosinus pleacă

de la valoarea 0 și ajunge la valoarea

minus 1 Prin urmare avem o funcție

descrescătoare în cadranul al treilea

funcția este crescătoare observăm

că există la acestor puncte cresc

și se apropie de valoarea zero

iar în cadranul al patrulea funcția

este crescătoare în concluzie funcția

cosinus este descrescătoare pe

intervalul 0 și crescătoare pe

intervalul p2p Deci pentru unghiurile

din cadranul 1 și 2 funcția este

descrescătoare iar pentru unghiurile

din cadranul 3 și 4 funcția este

crescătoare în continuare ne interesează

paritatea aceste funcții Vrem să

vedem ce se întâmplă pentru unghiuri

negative voi construi un om negativ

am construit acest unic negativ

aici avem unghiul minus Alfa observăm

că proiecția punctului corespunzător

pe axa o x coincide cu proiecția

punctului m pe axa o x prin urmare

cosinus de minus Alfa este egal

cu cosinus de Alfa Așadar funcția

cosinus este o funcție pară ca

și funcția Cine a fost Cine este

periodică având perioada principală

doi fii am văzut și în lecția trecută

că unghiurilor Alfa Alfa plus 2

pi respectiv al familiei 2pi le

corespund aceleași punct de pe

cercul trigonometric asta deoarece

pornind din acest punct m și efectuând

o rotație completă și în sens trigonometric

fie în sens negativ ajungem în

același punct M prin urmare cosinus

de Alfa are aceeași valoare cu

cosinus de Alfa plus 2 pi respectiv

cosinus de Alfa minus 2 pi Așadar

perioada principală a funcției

cosinus este 2 pi în continuare

se vede În graficul acestei funcții

avem în imagine graficul funcției

cosinus observăm că această funcție

ia valori cuprinse în intervalul

închis minus unu unu cosinus de

0 este 1 cosinus de pi supra 2

este 0 cosinus de pi este minus

unu cosinus de 3pi pe 2 este 0

cosinus de 2 pi este 1 se poate

observa și monotonia funcției vedem

Așadar că în intervalul 0 pi funcția

este descrescătoare iar pe intervalul

2 pi funcția este crescătoare de

asemenea funcția este periodică

având perioada principală doi fii

este suficient să trasăm graficul

unei funcții periodice pe un interval

de lungime a unei perioade de exemplu

pe intervalul 0 2 pai iar generarea

lui pe Dodo vinul de definiție

se face translate în duel la stânga

și la dreapta dea lungul axei o

x