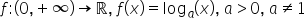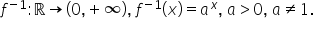Funcția logaritmică

Să considerăm funcția exponențială

definită pe r cu valori în intervalul

0 plus infinit exprimată prin legea

f de x egal cu 2 la puterea x funcția

exponențială este funcția în care

variabila x este la exponent elementul

3 va avea prin funcția f imaginea

8 pentru că 2 la puterea a treia

este egal cu 8 elementul 4 va avea

prin funcția f imaginea 16 pentru

că 2 la puterea a patra este egal

cu 16 spuneam în lecția trecută

că funcția exponențială este inversabilă

ne propunem în continuare să găsim

inversă aceste funcții mai exact

ne interesează funcția care duce

elementele din codomeniu în domeniu

care ar putea fi procedeul prin

care atașăm numărului 8 imaginea

3 având nume că 2 la puterea a

treia este egal cu 8 atunci din

definiția logaritmului unui număr

pozitiv avem că logaritm în baza

2 din 8 este egal cu 3 ori amintesc

că logaritmul este exponentul la

care ridică baza logaritmului pentru

a obține 8 în mod Analog avem că

logaritm în baza 2 din 16 este

egal cu 4 să reținem că logaritmul

este exponentul la care ridică

bază pentru a obține acel număr

astfel funcția care duce elementele

din codomeniul în domeniu va fi

f la minus 1 de y10 mul în baza

2 a numărului y dacă Revenim la

notația cu X avem că e f la minus

1 de x va fi egal cu logaritm în

baza 2 a numărului x Așadar inversă

funcției exponențiale este funcția

logaritmică în cazul general dacă

a este număr strict pozitiv a diferit

de 1 atunci funcția f definită

pe r cu valori în intervalul 0

plus infinit exprimată prin legea

f de x egal cu a la puterea x va

avea ca și inversă funcția f definită

pe intervalul 0 plus infinit cu

valori în R exprimată prin legea

f de x egal cu logaritm în bază

a a numărului x aceasta este funcția

logaritmică de bază a funcția logaritmică

este definită atâta vreme cât a

este număr strict pozitiv a diferit

de 1 trebuie să reținem că funcția

logaritmică există numai pentru

argumente pozitive în continuare

să vedem câteva proprietăți ale

funcției logaritmice dacă x este

egal cu 1 atunci f de 1 este egal

cu logaritm în baza a a numărului

1 și egal cu zero pentru că logaritmul

lui unu în orice bază este 0 putem

astfel trage concluzia că punctul

A de coordonate 1 și 0 aparține

graficului funcției logaritmice

să vedem în continuare monotonia

funcției logaritmice întotdeauna

inversă unei funcții păstrează

monotonia funcției directe astfel

dacă a este cuprins între 0 și

1 atunci funcția logaritmică este

strict descrescătoare pe domeniul

de definiție iar dacă a este mai

mare ca 1 atunci funcția logaritmică

este strict crescătoare Așadar

funcția logaritmică este strict

descrescătoare dacă bază este subunitară

și strict crescătoare dacă bază

este supraunitară funcția logaritmică

este bijectivă și inversabilă iar

inversa ei este funcția exponențială

în continuare să vedem câteva reprezentări

grafice să Reprezentăm grafic funcția

logaritmică e f de x egal cu logaritm

în bază 2 din x trasarea graficului

se va realiza prin puncte a făcut

astfel un tabel de valori pe prima

linie avem x pe a doua linie avem

fdx putem observa că este destul

de dificil să anticipăm care ar

fi acele valori ale lui x pentru

care putem calcula cu ușurință

logaritm în baza 2 a numărului

x Și atunci vom nota cu y f de

x și vom scrie relația logaritm

în baza 2 a numărului x egal cu

y sub formă exponențială această

egalitate se mai poate scrie exponențial

astfel 2 la puterea y egal cu x

Deci cele două relații exprimă

același lucru dar sunt scrise sub

forme diferite observăm că este

mai ușor să atribuim lui y Eva

lor și apoi să îl calculăm pe x

astfel Dacă y este minus 2 atunci

2 la puterea minus 2 va fi egal

cu 1 pe 4 Așadar x este egal cu

1 pe 4 iar y este minus doi Dacă

y este minus unu Avem doi la puterea

minus 1 egal cu 1 pe 2 x va fi

1 pe 2 iar y va fi minus 1 Dacă

y este egal cu 0 2 la puterea 0

este egal cu 1 avem punctul de

coordonate 1 0 iar Dacă y este

egal cu unu doi la unu a este egal

cu 2 palme avea punctul de coordonate

2 și 1 și acum vom reprezenta aceste

plante întru un reper cartezian

avem punctul de coordonate 1 pe

4 minus 2 apoi punctul de coordonate

1 pe 2 minus 1 punctul 1 0 și punctul

2 1 dacă un imprinto o linie continuă

aceste puncte obținem graficul

funcției logaritm în baza 2 din

x se poate observa că funcția este

strict crescătoare iar axa o y

sau dreapta de ecuație x egal cu

0 este asimptotă verticală pentru

graficul aceste funcții dacă Reprezentăm

în același reper cartezian și graficul

funcției 2 la puterea x Iată putem

observa că cele două grafice sunt

simetrice față de prima bisectoare

în continuare vom reprezenta grafic

funcția logaritm în baza 1 supra

radical din 3 a numărului x așa

cum spuneam mai devreme este destul

de dificil să anticipăm ce valori

să atribuim lui x pentru a putea

calcula cu ușurință acest logaritm

și atunci notăm f de x egal cu

y iar relația logaritm în baza

1 pe radical din 3 a numărului

x egal cu y se va scrie sub formă

exponențială astfel 1 supra radical

din 3 ridicat la puterea y egal

cu x în continuare putem scrie

această egalitate sub forma radical

din 3 la minus 1 și totul la y2j

adică el din 3 la minus y egal

cu x și acum a trebui în valori

lui y Dacă y este egal cu 2 radical

din 3 la puterea minus 2 va fi

egal cu 1 supra radical din 3 la

a doua Deci 1 pe 3 astfel obținem

punctul de coordonate 1 pe 3 și

2 Dacă y este egal cu 1 avem radical

din 3 la minus 1 și egal cu 1 supra

radical din 3 pentru x egal cu

1 pe radical din 3 am obținut yii2

el cu 1 Dacă y este egal cu zero

vom avea a radical din 3 la puterea

0 și egal cu unu îmi trece în tabel

punctul de coordonate 1 0 iar Dacă

y este egal cu minus unu avem radical

din 3 la minus minus unu deja adică

el din 3 la unuia egal cu radical

din 3 avem punctul de coordonate

radical din trei și minus unu să

mai luăm o valoare pentru a egal

cu minus 2 avem radical din 3 la

minus minus 2 adică radical din

3 la a doua și egal cu 3 am obținut

punctul de coordonate 3 minus 2

reprezenta aceste puncte un reper

cartezian avem punctul de coordonate

1 pe 3 2 punctul de coordonate

1 0 radical din 3 și minus 1 și

punctul 3 minus 2 unim cele patru

puncte albastre printr o linie

continuăm Iată acesta este graficul

funcției logaritm în baza 1 pe

radical din 3 din x se poate observa

în cazul în care baza logaritmului

este subunitară funcția logaritmică

este strict descrescătoare și în

această situație dreapta de ecuație

x egal cu 0 este asimptotă verticală

pentru graficul funcției