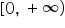Funcția putere cu exponent natural
Tag-uri
Partajeaza in Google Classroom

Transcript
în unele formule ce exprimă arii
și volume întâlnim funcția putere
de exemplu aria pătratului este
latura la puterea a doua sau volumul
cubului este latura la puterea
a treia o funcție f definită pe
r cu valori în R f de x egal cu
x la n unde n este număr natural
nenul se numește funcția putere
Dacă n este egal cu 1 obține Funcția
de gradul întâi este x egal cu
x iar dacă n este egal cu 2 obține
Funcția de gradul al doilea f de
x egal cu x la pătrat în cele ce
urmează vom discuta a proprietățile
funcției putere în cazul în care
n este număr par respectiv impar
Dacă n este număr par atunci acesta
va fi de forma 2k unde k este număr
natural nenul iar în acest caz
fdx va fi egal cu x la puterea
a 2 ca să verific în continuare
paritatea acestei funcții pentru
aceasta vom calcula f de minus
x vom avea minus x la puterea a
2 ca orice număr negativ ridicat
la o putere pară devine pozitiv
în consecință vom avea egal cu
x la puterea 2 ca și egal cu fdx
am obținut că e f de minus x este
egal cu f de x în consecință este
o funcție pară Așadar graficul
aceste funcții va fi Simetric față
de axa o y funcția f nu este monotona
pe tot domeniul de definiție însă
există intervale de monotonie pentru
a studia monotonia aceste funcții
vom considera mai întâi primul
caz în care X1 și X2 aparțin intervalului
minus infinit 0 astfel încât x
1 să fie mai mic decât x 2 nu am
ridicat la o putere pară această
inimă litate și vom obține că x
1 la puterea a 2 ca este mai mare
decât x 2 la puterea a 2 ca pentru
a înțelege mai bine acest aspect
Iată un exemplu concret știind
că A minus 4 este mai mic decât
minus 3 Dacă ridicăm la o putere
pară această inegalitate vom avea
căminul 4 la a doua este mai mare
decât minus 3 la a doua pentru
că 16 este mai mare decât 9 obținem
Așadar că e f de x 1 este mai mare
decât f de x 2 în consecință funcția
f este strict descrescătoare pe
intervalul minus infinit 0 să vedem
ce se întâmplă în cazul în care
X1 și X2 aparține intervalului
0 infinit Considerăm x 1 mai mic
decât x 2 dacă ridicăm la o putere
pară această inegalitate vom avea
că x 1 la 2 k este mai mic decât
x 2 la puterea 2k atunci când Numerele
sunt pozitive relația de ordine
dintre acestea se păstrează prin
ridicare la putere obținem Așadar
că f de x 1 este mai mic decât
f de x 2 în consecință f este strict
crescătoare pe intervalul 0 plus
infinit în continuare vom studia
semnul funcției pentru x egal cu
0 f de x va fi egal cu zero Dacă
x y au valori de la minus infinit
la 0 funcția are valori pozitive
pentru că orice număr negativ ridicat
la o putere pară devine pozitiv
iar în cazul în care x este mai
mare ca 0 și funcția f de x va
avea valori pozitive observăm Așadar
că funcția ia doar valori pozitive
Deci graficul acesteia va fi situat
deasupra axei o x și va trece prin
punctul de coordonate 0 0 în continuare
vom reprezenta grafic două funcții
particulare f de x egal cu x la
a doua și f de x egal cu x la a
patra am făcut un tabel de Valori
și în continuare vom calcula valorile
funcției f de x egal cu x la a
doua pentru x egal cu 0 f de 0
este 0 1 la a doua este 1 3 supra
2 la a doua este 9 pe 4 iar 2 la
a doua este 4 minus 1 la a doua
este 1 minus 3 supra 2 la a doua
este 9 pe 4 minus 2 la a doua este
egal cu 4 să calculăm și valorile
funcției f de x egal cu x la a
patra pentru x egal cu 0 funcția
are valoarea 0 1 la a patra este
1 3 supra 2 la puterea a patra
va fi 81 pe 16 2 la a patra este
16 minus 1 la a patra este 1 minus
3 supra 2 la a patra este 81 pe
16 și minus 2 la a patra este egal
cu 16 graficul acestor funcții
se va obține prin puncte adică
unim cu o linie continuă punctele
ale căror coordonate sunt valorile
din acest tabel Iată graficul funcției
f de x egal cu x la a doua observăm
că această parabolă trece prin
punctul de coordonate 0 0 și prin
punctele de coordonate minus unu
unu respectiv unu unu așa cum spuneam
mai devreme funcția este strict
descrescătoare pentru x lume valori
de la minus infinit până la 0 și
strict crescătoare pentru x luni
valori de la 0 la plus infinit
de asemenea remarcăm faptul că
axa o y este axa de simetrie pentru
graficul acestei funcții să vedem
în continuare în graficul funcției
f de x egal cu x la a patra Iată
observăm că și eu această parabolă
trece prin punctul de coordonate
0 0 și prin punctele de coordonate
minus unu unu respectiv unu unu
de fapt toate parabolele de forma
x la puterea 2 k trec prin punctele
de coordonate minus unu unu și
unu unu Cu cât exponentul funcție
este mai mare cu atât ramurile
parabolei sunt mai apropiate de
axa o y o serveam că funcția f
de x egal cu x la 2 k nu este bijectivă
însă dacă luăm în considerare doar
o jumătate din această parabolă
funcția de vine bijectivă astfel
pentru x luni ma lor de la minus
infinit la 0 și pentru y2 de la
0 la plus infinit funcția este
bijectivă deci inversabilă de asemenea
se obține o funcție bijectivă și
pentru x sunt valori de la 0 la
plus infinit și codomeniul 0 plus
infinit în continuare dorim să
studiem proprietățile funcției
putere cu exponent natural în cazul
în care n este număr impar Dacă
n este impar atunci n se poate
scrie sub forma 2k plus 1 unde
ca este număr natural nenul iar
în această situație f de x egal
cu x la puterea 2 k plus unu pentru
a studia paritatea funcției vom
calcula f de minus x și avem minus
x la puterea a 2 ca plus unu un
număr negativ la o putere impară
își păstrează semnul minus în consecință
vom avea minus x la puterea a 2
ca plus 1 și egal cu minus ftx
obținem astfel că funcția f este
o funcție impară așa dar pentru
n par funcția este pară iar în
azil în care an este impar funcția
este impară în această situație
graficul funcției va fi Simetric
față de originea reperului cartezian
să studiem în continuare monotonia
aceste funcții numerele negative
ridicate la putere impară își păstrează
semnul prin urmare putem studia
în monotonia acestei funcții pe
tot domeniul de definiție ar fi
Așadar X1 și X2 numere reale astfel
încât x unu să fie mai mic decât
x 2 dacă ridicăm inegalitatea la
puterea 2 ca plus 1 vom avea X1
la 2k plus 1 mai mic decât x 2
la puterea 2 k plus 1 obținem astfel
că f de x 1 este mai mic decât
f de x 2 în consecință funcția
f este strict crescătoare în continuare
așa să vedem semnul aceste funcții
pentru x egal cu zero funcția ia
valoarea zero pentru x luni valori
negative funcția f de x are De
asemenea valori negative pentru
că orice număr negativ la o putere
impară rămâne negativ iar pentru
x valori mai mari ca 0 funcția
are valori pozitive putem astfel
trage concluzia că pentru valorile
lui x mai mici decât 0 graficul
va fi situat sub axa o x iar pentru
acele valori ale lui x mai mare
ca 0 graficul va fi situat deasupra
axei o x de asemenea graficul trece
prin punctul de coordonate 0 0
în continuare vom reprezenta grafic
funcția f de x egal cu x la puterea
a treia vom face un tabel de Valori
pentru x egal cu zero avem 0 la
puterea a treia egal cu 0 1 la
a treia este 1 3 supra 2 la puterea
a treia este 27 supra 8 și 2 la
a treia este egal cu 8 minus 1
la a treia este minus 1 minus 3
supra 2 la a treia este minus 27
supra 8 și minus 2 la a treia este
egal cu minus 8 graficul funcției
se obține unind printr o linie
continuă punctele ale căror coordonate
sunt valorile din acest tabel Iată
graficul funcției această parabolă
se numește parabolă cubică toate
parabolele de forma x la puterea
2 ca plus 1 trec prin punctele
de coordonate minus 1 minus 1 0
0 și 1 1 800 funcția este strict
crescătoare pe tot domeniul de
definiție iar punctul O este centrul
de simetrie pentru graficul acestei
funcții

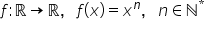
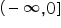 și strict crescătoare pe
și strict crescătoare pe