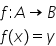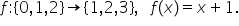Funcții (definiție, terminologie)

Vrem să vedem acum Ce este aceea

o funcție și o Vom definit și apoi

vedem Și ce terminologie vom folosi

ce denumiri folosim în cadrul funcțiilor

o funcție exprima sau Realizează

o corespondență între două variabile

sau putem spune că o funcție Realizează

o corespondență între elementele

a două mulțimi acum când spunem

că funcția Realizează o corespondență

între două variabile ne referim

la faptul că dacă ni se dă de exemplu

o variabilă să o notăm cu x atunci

printr o anumită lege sau regulă

o să scriu aici printro regulă

sau lege se obține o altă variabilă

să o notăm cu y și clar această

variabilă y y depinde de x pentru

că Iată ne intră variabilă x printru

o lege de transformare să îi spunem

așa printr o anumită regulă de

calcul se obține variabila y care

depinde de ce ai intrat adică depinde

de x acum ca să arătăm că e depinde

de x putem să trecem aici în paranteză

x y z x putem să folosim în locul

lui X și Y ce litere vrem însă

să știți că în general se folosește

aici f d x Deci evaluarea care

se obține se notează cu e f de

x și chiar o să șterg pe y din

X dar se folosește destul de des

5dx și pentru moment o să lăsăm

f d x bun și avem acum o corespondență

între două variabile Haide să dăm

concret un exemplu de funcție Deci

avem variabila x o notăm tot cu

X iar regula sau legea este aceasta

x plus patru deci ne intră variabila

x aici avem variabila ia tălpi

x și prin regula dată aici adică

prin x plus 4 se obține o altă

variabilă și anume f de x și chiar

o să șterg și o să scriem aici

că regula sau legea pentru exemplul

nostru este x Haide să scriem tot

cu alb este x plus 4 bun și concret

să facem câteva calcule dacă în

locul lui x 3 cm valoarea doi de

exemplu Păi intră doi Da intră

numărul 2 prin această lege si

Vom avea în locul lui X trecem

doi Deci vom avea doi adunat cu

4 și vom obține Cât Păi 2 cu 4

ne dă adică FD ceai intrat adică

f de 2 este 6 alt exemplu să luăm

acum numărul 5 a intrat valoarea

5 prin această lege sau regulă

Cum transformăm Păi din cinci vom

avea 5 adunat cu 4 și rezultatul

pe care îl obținem este nouă Deci

o mulțime aici 9 sau dacă intră

30 da vom obține prin această transformare

avem aici x plus 4 adică 30 adunat

cu 4 și o să ne dea valoarea 34

de ce ai intrat o variabilă x și

am obținut fdx Iată a intrat numărul

2 prin această transformare la

am obținut pe 6 evident că în exerciții

nu o să folosim asta scriere Dar

vom folosi aceste notații Deci

dacă lui x y am dat valoarea 2

atunci e f d 2 cu cât este egal

în locul lui x 3 cm 2 și aici Avem

doi adunat cu 4 și rezultatul este

șase iar E F de 2 Da ne dă șef

de ce a intrat adică de 2 nea dat

șase nu am scris nimic nou dacă

x este 5 Cât va fi f de 5 pâine

uităm la lege f25 este cinci de

notăm 5 adunat cu 4 și o să obținem

nou facut ma de 30 egal cu 30 de

sigle cu 30 adunat cu 4 Rezultatul

este 34 Deci asta e se realizează

corespondența între două variabile

Da înaintea variabila x la am obținut

pe fdx și valorile funcției f în

aceste numere 2 5:30 sunt acestea

scrise cu albastru acum trebuie

să stabilim și mulțimea în care

variabila ia valori aici noi am

avut pentru x am dat valorile 2

5:30 putem Să considerăm chiar

această mulțime Avem doi 5:30 și

o să notăm astfel e f două puncte

și spunem că funcția f că așa notată

ef este definită pe această mulțime

în care variabila iau valori și

duce această mulțime să spunem

așa între o altă mulțime aici trebuie

să mulțimea care conține valorile

returnate de funcție Păi funcția

f ce valori returnează ce am scris

aici cu albastru 6 9 și 34 asta

înseamnă că mulțimea pe care o

Vom muta aici Trebuie neapărat

să conțină aceste numere 6 9 și

34 și putem să trecem aici de exemplu

6 8 9 și 34 această mulțime conține

aceste trei numere sau putem să

Scrie mulțimea formată doar din

aceste trei numere 6 9 și 34 sau

Am putea să scriem mulțimea R că

mulțimea aer conține numerele 6

9 34 dar dacă am scrie doar pe

6 și pe 9 Mai e corect Nu pentru

că funcția noastră returnează și

valoarea 34 Deci această mulțime

Trebuie neapărat să conțină Toate

aceste valori deci aici nu e corect

și o să păstrez această formă ca

să fie clar că ce avem aici această

mulțime nu trebuie neapărat să

fie mulțimea returnată de funcție

dar formată doar din aceste numere

și această mulțime Trebuie doar

să conțină valorile pe care funcțiile

returnează Deci o să șterg aici

și acum Haideți să ne ocupăm puțin

de denumirile care se folosesc

mulțimea în care variabila ia valori

se numește adică această mulțime

se numește domeniu sau domeniul

de definiție aici variabil ia valori

iar cea de a doua mulțime aceasta

se numește codomeniu codomeniu

este mulțimea în care funcția ia

valori iar legea Care este data

aici această regulă de calcul se

numește lege de corespondență aici

mai am de scris funcția printr

o formulă însă o funcție se poate

descrie și printru un desen și

în cazul nostru putem să folosim

un asemenea destin aici vom trece

domeniul funcției adică mulțimea

în care x iau valori în care variabilă

ia valori chiar aici și vom trece

de fapt ai de să scrie mai ceva

mai departe iar Aici vom trece

codomeniul mulțimea în care funcția

ia valori ce avem la domeniu Păi

Iată avem aici 2 5:30 să le trecem

avem numerele 2 5 și 30 Iar codomeniul

avem 6 8 9 34 chiar o să scriu

cu albastru avem 6 8 9 și 3434

funcția f ce corespondență ce corespondențe

de fapt realizează numărul 2 merge

în 6 pentru că f de 2 ne dă 6 deci

venim aici notăm 2 mergem 6 5 merge

în 9 5 merge iar 30 merge în 34

din acest desen ce se vede că de

fapt e o funcție Realizează o corespondență

între elementele a două mulțimi

de aceea am spus la început că

funcția poate fi privită și ca

o corespondență între două variabile

cum am avut aici sau ca o corespondență

între elementele a două mulțimi

însă foarte mare atenție nu orice

corespondență este o funcție ca

să avem întradevăr o funcție corespondența

trebuie făcută a astfel încât fiecărui

element din prima mulțime adică

din domeniu să îi corespunde un

singur element în a doua mulțime

adică în codomeniu Și aici este

îndeplinită această condiție fiecare

element din prima mulțime are corespondent

în cea de a doua și acest corespondenți

unic adică 2 merge doar în șase

nu merge și în șase și în opt sau

să meargă și în șase și nouă Dacă

era și atunci nu mai aveam funcție

și acum Haideți să vedem câteva

exemple să vedem care dintre ele

Descrie o funcție care nu și să

vedem de ce să vedem dacă aici

avem o funcție avem numerele 1

8 13 în a doua mulțime 2 și 5 un

număr gen 213 la Recaș e corespondent

pe 5 însă 8 nu merge nici un număr

din a doua mulțime Deci avem sau

nu avem o funcție nu este funcție

pentru că 8 nu are nici un corespondent

în cea de a doua mulțime ca să

fie funcție trebuia ca fiecare

element din prima mulțime să aibă

un corespondent în cea de a doua

dar aici 0 și trei și unu și patru

zero Merge m13 merge în unu pe

poate unii dintre voi sunteți să

spună că nici în această situație

nu avem o funcție pentru că și

0:03 merg în unu nu se stie Este

fals ca să fie funcție trebuie

ca fiecare element din prima mulțime

să aibă un singur în cea de a doua

și Acest lucru se întâmplă aici

Iată 0 are un singur corespondent

îl are pe 1 3 are și el tot un

singur corespondent îl are pe unul

nu are importanță faptul că și

0:03 au același corespondent Deci

aici avem întradevăr o funcție

următorul exemplu avem 0 360 1

4 și 2 Păi 0 are ca și corespondenți

și pe 1 și pe 4 din start ce avem

aici nu este funcție pentru că

fiecare element din această mulțime

trebuie să aibă un singur corespondent

în cea de a doua Iar 0 are 2 corespondent

Deci notăm aici că nu este funcție

pentru că elementul 0 are 2 corespondenți

ultimul exemplu avem aici o funcție

nu mai este dată prin desen funcția

notată G pe mulțimea Maria Dan

Alex avem aici numele a trei persoane

cu valori în l unde a este mulțimea

formată din lunile anului ianuarie

februarie martie și așa mai departe

decembrie GLX este luna de naștere

a lui x aceasta este legea cu alte

cuvinte g de Maria Ce înseamnă

înseamnă lună de naștere a Mariei

g de Dani este luna de naștere

a lui Dan și așa mai departe este

aceasta o funcție Fiecare om se

naște întru anumită lună așa și

Maria Dan și Alex au un singur

corespondent în această mulțime

pentru că nu putem să spunem că

Maria sa născut în ianuarie și

în februarie însă putem spune că

Maria sa născut de exemplu în ianuarie

Dan sa născut în martie iar Alex

poate că se născut tot în ianuarie

de fapt avem o mulți o funcție

pardon pentru că fiecare element

din prima mulțime are un singur

corespondent în cea de a doua de

ceai de să notăm că avem aici o

funcție prin urmare ca să facem

un rezumat o funcție poate fi descrisă

printru un desen mare atenție ca

lege de corespondență să fie corectă

ca să avem întradevăr 8 sau printre

o formulă Iată cum am avut prima

dată îmi plac primul exemplu sau

să știți că putem să exprimăm o

să descriem o funcție și printru

un tabel de exemplu avem aici x

și vom nota valorile lui x pe această

linie iar Aici valorile returnate

de funcții adică f de x pe a doua

linie pe prima linie vom trece

valorile din domeniu adică 2 5:30

2 5:30 iar pe a doua linie valorile

pe care le returnează funcția adică

aici vom avea f de doi care ne

dă 6 aici sub 5 vom avea sd5 adică

9 iar sub 30 vom avea f de 30 adică

34 Deci o funcție poate fi descrisă

prin una dintre aceste variante