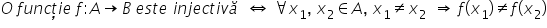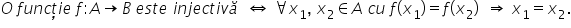Funcții injective

știm că o funcție este o relație

între două mulțimi care Asociază

fiecărui element din domeniu un

singur element din codomeniu asta

înseamnă că atunci când Reprezentăm

graficul funcției dacă ducem o

paralelă la axa o intrec aceasta

va intersecta graficul funcției

intru un singur punct în cazul

în care paralela intersectează

graficul în două puncte atunci

nu avem o funcție Așadar graficul

din partea dreaptă nu poate fi

graficul unei funcții o categorie

importantă de funcție este cea

a funcțiilor bijective o funcție

se numește bijectivă dacă este

injectivă și surjectivă Haideți

să vedem în continuare Ce este

o funcție injectivă avem în imagine

trei funcții reprezentate prin

aceste diagrame pentru prima funcție

avem următoarea corespondență lui

unu e se asociază numărul 4 numărul

lui 4 se asociază 7 iar numărul

lui 6 îi corespunde nouă o expresie

analitică ce ar putea descrie prima

corespondență este formula f de

x egal cu x plus 3 pentru a doua

funcție avem următoarele corespondențe

numărului minus doi îi corespunde

patru numărului doi îi corespunde

patru numărului minus 3 îi corespunde

9 iar numărul lui 3 îi corespunde

nouă această lege de corespondență

sar putea exprima analitic folosind

formula f de x egal cu x la pătrat

iar pentru ultima funcție avem

următoarele corespondențe numărul

lui unu e se asociază 1 numărului

minus unu îi corespunde 1 lui 3.000

corespunde trei lui minus 3y corespunde

trei numărului 5 îi corespund de

5 iar numărului minus 5 a corespunde

5 formula care poate descrie această

corespondență este f de x egal

cu modul din x observăm că pentru

funcția f de x egal cu x plus trei

argumente distincte generează imagini

distincte aspecte ce nu are loc

în cazul celorlalte două funcții

Iată la a doua funcție avem argumente

distincte minus doi și doi care

generează aceeași imagine 4 sau

3 și minus 3 care generează aceeași

margine 9 și la a treia funcție

avem imagini egale generate de

argumente diferite Iată numerele

unu și minus nu au aceeași imagine

1 numerele 3 și minus 3 au aceeași

margine 3 iar 5 și minus 5 au aceeași

imagine 5 o funcție se numește

funcție injectivă sau injecție

Dacă și numai dacă două elemente

diferite din domeniu au imagini

diferite în codomeniu astfel prima

funcție este o funcție injectivă

însă celelalte două funcții nu

sunt funcții injective pentru că

avem elemente în codomeniu spre

care se îndreaptă câte două săgeți

Așadar o funcție este injectivă

sau injecție Dacă și numai dacă

oricare ar fi X1 și X2 din ei cu

X1 diferit de X2 să avem că fdx

1 este diferit de f de x 2 o altă

definiție echivalentă cu aceasta

și următoarea este injectivă dacă

și numai dacă oricare ar fi X1

și X2 elemente din domeniu cu este

X1 egal cu f de x 2 să avem că

x 1 este egal cu x 2 de cele mai

multe ori se recomandă aplicarea

acestei definiții pentru că e mult

mai ușor să demonstrăm egalități

decât relații ce conțin simbolul

diferit o funcție nu este injectivă

dacă putem pune în evidență două

argumente distincte astfel încât

imaginile lor să fie egal în exemplele

de mai sus am avut funcții definite

pe mulțimi finite Haideți acum

să extindem aceste funcții la aer

și să studiem injectivitatea lor

pe baza acestor definiții prima

funcției este f definită pe r cu

valori in r f de x egal cu x plus

3 vom alege două valori X1 și X2

din R și presupunem că f de x 1

este egal cu f de x doi va trebui

să arătăm că și x 1 este egal cu

x 2 fdx 1 este x 1 plus 3 iar f

de x 2 este x 2 plus 3 Dacă scădem

din ambii membri ai Egalității

numărul 3 obținem că x 1 este egal

cu x 2 iată că pornind de la egalitatea

fdx 1 egal cu f de x doi am arătat

că are loc și o relație de egalitate

între argumentele funcției în consecință

putem trage concluzia că funcția

f este injectiva pentru a doua

funcție f de x egal cu x pătrat

pornim de la relația f de x 1 este

egal cu f de x doi și vrem să verificăm

dacă X1 este egal cu X2 fdx unul

este X1 la pătrat iar f de x 2

este egal cu X2 la pătrat trece

totul în primul membru și obținem

X1 la pătrat minus X2 la pătrat

egal cu 0 Descompune în factori

și avem x 1 minus x 2 pe lângă

x 1 plus x 2 este egal cu 0 un

produs este 0 dacă unul din factori

este 0 Așadar avem X1 egal cu x

2 sau x unu egal cu minus x 2 deja

dată că nu întotdeauna are loc

o egalitate între argumentele funcției

așa dar având în vedere că f de

x 1 este egal cu f de x 2 conduce

la relația X1 egal cu minus x 2

înseamnă că funcția f nu este o

funcție injectivă pentru funcția

f de x egal modul din x procedăm

asemănător pornind de la egalitatea

fdx 1 egal cu este x2 și vrem să

verificăm dacă X1 este egal cu

x 2 avem modul din x 1 egal cu

modul din x 2 dar aceasta egalitate

va conduce la relația X1 egal plus

minus X2 în consecință funcția

f nu este funcție injectivă atunci

când studiem injectivitatea unei

funcții este important să verificăm

și domeniul de definiție Iată funcția

f de x egal cu x pătrat nu este

injectivă pe aer însă dacă domeniul

de definiție este mulțimea numerelor

naturale atunci obținem o funcție

injectivă o altă metodă de a studia

injectivitatea unei funcții este

metoda grafică Haideți să vedem

cum arată graficele acestor funcții

acestea sunt graficele celor trei

funcții iar pentru a studia injectivitatea

ducem paralele la axa o x dacă

orice paralelă la axa o x dusă

prin elementele codomeniului taie

graficul funcției în cel mult un

punct atunci funcția este injectivă

dacă paralela taie graficul în

două puncte atunci acea funcție

nu este funcție injectivă în continuare

Haideți să studiem injectivitatea

unei funcții definite pe ramuri

avem următorul exercițiu Arătați

că funcția de mai jos este injectivă

f definită pe r cu valori in r

f de x egal cu 3X pătrat plus 2

dacă x este mai mic sau egal cu

0 și minus x plus doi dacă x este

mai mare ca 0 pentru acest tip

de exerciții vom lua în considerare

trei cazuri posibile primul caz

în care se alege X1 și X2 din primul

interval minus infinit 0 al doilea

caz alege mix 1 și x 2 din intervalul

0 infinit și al treilea caz în

care x 1 este mai mic sau egal

cu 0 și x 2 este mai mare ca 0

începem Așadar cu primul caz fie

X1 și X2 din intervalul minus infinit

0 astfel încât f de x 1 să fie

egal cu f de x doi trebuie să demonstrăm

că x 1 este egal cu x 2 și avem

trei X1 la pătrat plus 2 egal cu

3 x 2 la pătrat plus 2 scădem 2

din ambii membri și obținem 3 x

1 la pătrat egal cu 3 x 2 la pătrat

împărțim la 3 și avem X1 la pătrat

egal cu X2 la pătrat dar având

în vedere că X1 și X2 sunt din

intervalul minus infinit 0 înseamnă

că X1 va fi egal cu x 2 De ce am

pornit de la egalitatea fdx 1 egal

cu f de x 2 și am arătat că X1

este egal cu x 2 al doilea caz

fie X1 și X2 din intervalul 0 plus

infinit astfel încât fdx 1 este

egal cu f de x 2 trebuie să demonstrăm

că x 1 este egal cu x 2 ef tx1

este minus x 1 plus 2 iar f de

x 2 este minus x 2 plus 2 scădem

numărul 2 din Ami membrii și avem

minus x unu egal cu minus x 2 înmulțim

cu minus 1 și obținem X1 egal cu

x 2 și al treilea cos fie X1 din

intervalul minus infinit 0 și x

2 din intervalul 0 infinit observăm

Așadar că X1 și X2 fac parte din

intervale diferite înseamnă că

X1 este diferit de X2 și atunci

va trebui să arătăm că f de x 1

este diferit de acting doi vom

presupune prin absurd că f de x

1 poate să fie egal cu f de x 2

înseamnă că f de x 1 este 3 x 1

la pătrat plus 2 egal cu minus

x 2 plus 2 Deci trei X1 la pătrat

este egal cu minus X2 X1 face parte

din intervalul minus infinit 0

înseamnă că X1 la pătrat este mai

mare sau egal cu 0 Deci membrul

stâng este un număr mai mare sau

egal cu 0 x 2 este număr pozitiv

înseamnă că minus x 2 este negativ

având în vedere că numărul din

membrul stâng este mai mare sau

egal cu 0 iar numărul din membrul

drept este strict negativ înseamnă

că aceasta egalitate este imposibilă

Așadar presupunerea făcută este

falsă În consecință f de x 1 este

diferit de e f d x 2 am arătat

în acest mod că funcția f este

injectivă o altă modalitate de

a studia injectivitatea unei funcții

este verificarea monotoniei acesteia

întrucât are loc următoarea teoremă

fie f o funcție definită pe a cu

valori în b dacă ia fi este strict

monotonă atunci f este injectiva