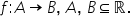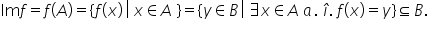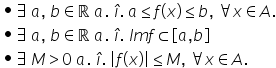Funcții mărginite (teorie)
Tag-uri
Partajeaza in Google Classroom

Transcript
înainte de a discuta despre funcții
mărginite aș vrea să reamintesc
puțin noțiunea de imagine a unei
funcții pe care sa mai întâlnită
și în gimnaziu dacă avem o funcție
f definită pe a cu valori în b
unde a și b sunt submulțimi ale
lui e atunci timp din definiția
unei funcții că fiecărui element
x din ei îi asociem prin funcția
e un condiment y din b unde reprezintă
valoarea funcției calculată în
punctul x y se mai numește și imaginea
lui x prin funcția f atunci mulțimea
tuturor imaginilor elementelor
din a parte denumirea de imaginea
funcției i se notează cu e f sau
se mai poate înota și cu F da această
mulțime este inclusă în mulțimea
b să reținem Așadar că imaginea
unei funcții este o submulțime
a codomeniului funcției f imaginea
funcției f se mai poate scrie și
astfel mulțimea formată din acele
elemente din b cu proprietatea
că există x element din a astfel
încât f de x egal cu y bine Zi
încă o dată faptul că este a este
o submulțime a codomeniului funcției
Așadar trebuie făcută distincția
între imaginea funcției și codomeniul
acesteia să vedem un exemplu fie
funcția f definită pe r cu valori
în R f de x egal cu minus 1 dacă
x este pozitiv și unul dacă x este
negativ atunci imaginea funcției
este mulțimea valorilor funcției
unde x aparține lui r innomed ce
funcție a poate lua bara acestei
două valori minus 1 și 1 înseamnă
că imaginea funcției f este chiar
mulțimea formată din elementele
minus 1 și 1 iar aceasta este inclusă
în aer Așadar să facem distincție
între imaginea funcției și codomeniul
acesteia mai exact între imagine
și codomeniu există o relație de
incluziune să vedem și eu o interpretare
geometrică să ne prezentăm mândro
sistem cartezian x o y în graficul
unei funcții avem sistemul x o
y și Să presupunem că avem o funcție
al cărei grafic arată așa elementele
din mulțimea a se reprezintă pe
axa o x iar elementele din mulțimea
b se reprezintă pe axa o y Așadar
pentru a reprezenta pe axa o x
mulțimea A mare ar trebui să proiectăm
graficul acestei funcții pe axa
o x Așadar vom proiecta graficul
funcției pe axa o x putem să proiectăm
și câteva puncte intermediare Iată
și acum un in state aceste proiecții
obține mulțimea A mare domeniul
de definiție al funcției pentru
a găsi acum mulțimea valorilor
funcției f adică mulțimea f de
a proiect în graficul funcției
pe axa o y putem să proiectăm și
câteva puncte intermediare și un
index este proiecții obținem imaginea
funcției f Iată această mulțime
este de a dacă notăm aceste două
numere de pe axa o y cu a mic și
b mic observăm Așadar că imaginea
funcției f sau f d a este intervalul
închis a b aceasta a fost o interpretare
geometrică așa cum Haideți în continuare
să discutăm despre funcții mărginite
evident că există o strânsă legătură
între noțiunea de funcție mărginită
și cea de imagine a funcției să
vedem Așadar în continuare definiția
funcțiilor mărginite fie f definită
pe a cu valori în b o funcție atunci
f este mărginită dacă există două
numere reale a și b astfel încât
a să fie mai mic sau egal decât
f de x mai mic sau egal cu b oricare
ar fi x din a Așadar mulțimea valorilor
funcției f este mulțime mărginită
cuprinse între numerele a și b
această definiție se mai poate
scrie și astfel există două numere
reale a și b astfel încât imaginea
funcției să fie inclusă în intervalul
închis ab sau o a treia definiție
echivalentă există m număr pozitiv
astfel încât modul din f de x să
fie mai mic sau egal cu m oricare
ar fi x din a să vedem în continuare
și interpretarea geometrică am
reprezentat cu galben graficul
unei funcții între un sistem de
axe x o y proiect în graficul funcției
pe axa o x obținem domeniul de
definiție al funcției adică mulțimea
A proiect în graficul acestei funcții
pe axa o y obținem mulțimea valorilor
funcției f sau imaginea funcției
f dacă e f e este funcție mărginită
atunci există două numere a și
b situate pe axa o y ia tele astfel
încât mulțimea valorilor funcției
f să fie cuprinsă între a și b
cu alte cuvinte funcția f este
mărginită dacă graficul funcției
este cuprins între două drepte
paralele cu Axa o x aceste două
drepte au ecuațiile yigal cu ei
și y egal cu b Așadar dacă funcția
a fi este mărginită are loc această
relație imaginea funcției f este
inclusă în intervalul închis a
b unde a și b sunt numere pe axa
o y în secvența următoare mă face
câteva aplicații în care vom studia
mărginirea unor funcții