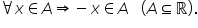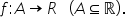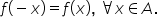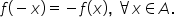Funcții pare, impare

înainte de a defini funcțiile pare

și impare ar trebui să definim

noțiunea de mulțime simetrică Iată

o mulțime A se numește simetrică

dacă pentru orice x din a și minus

x aparține lui a să dăm câteva

exemple de mulțimi simetrice de

exemplu intervalul minus doi doi

este o mulțime simetrică intervalul

minus infinit minus 6 reunit cu

6 plus infinit Este o mulțime simetrică

pentru că Iată se respectă această

proprietate este de asemenea mulțime

simetrică și câteva contra exemple

intervalul minus 2 3 nu este mulțime

simetrică pentru că avem de exemplu

numărul 3 care aparțin aceste mulțimi

însă opusul acestuia minus 3 nu

aparține intervalului un contraexemplu

intervalul 0 infinit Nu este mulțime

simetrică observăm că aici Avem

doar numere pozitive iar opusele

acestora nu aparțin intervalului

și acum putem să definim în continuare

funcțiile pare și impare Deci lucrurile

sunt clare dacă e f de minus x

este egal cu f de x atunci funcția

este pară iar dacă f de minus x

este egal cu minus f de x atunci

funcția este impară să vedem câteva

exemple avem funcția f definită

pe r cu valori în R observăm că

domeniul este o mulțime simetrică

e f de x egal cu 2 minus x pătrat

Haideți să verificăm dacă aceasta

este o funcție pară sau impară

trebuie Așadar să calculăm f de

minus x pentru aceasta o să îl

Înlocuim pe x cu minus x și o să

avem doi minus minus x la pătrat

egal cu 2 minus minus x la pătrat

de vine x la pătrat pentru că avem

o putere pară Și iată ce am obținut

Aici este chiar funcția inițială

fdx observăm Așadar că f de minus

x este egal cu f de x prin urmare

funcția este pară un alt exemplu

avem funcția f definită pe r cu

valori in r f de x egal cu x la

a treia plus x trebuie să calculăm

f de minus x scuzați f de minus

x egal o să îl Înlocuim pe x cu

minus x și obținem minus x la a

treia plus minus x exponentul este

impar Așadar se păstrează semnul

minus minus x dacă îl dăm acum

pe minus factor comun obține minus

pe lângă x la a treia plus x iată

în paranteză avem funcția inițială

însă avem un minus în fața parantezei

așa dar putem să scriem în continuare

egal cu minus fdx am obținut Așadar

că e f de minus x este egal cu

minus fdx prin urmare este impară

și un ultim exemplu f definită

pe r cu valori in r f de x egal

cu 6 x minus 3x pătrat vom calcula

f de minus x avem șase ori minus

x minus trei ori minus x la pătrat

egal cu minus 6x minus 3 minus

x la pătrat de vine x la patrat

însă rezultatul nu este identic

cu funcția inițială să dacă îl

dăm pe minus factor comun și obținem

minus pe lângă 6x plus 3x pătrat

iar dacă nici în formă aceasta

nu am ajuns la funcția inițială

prin urmare această funcție nu

este nici pară și nici impară Așadar

există funcții care nu sunt nici

pare și nici impare și acum haide

să vedem în continuare câteva proprietăți

grafice ale funcțiilor pare respectiv

impare pornind de la funcția dat

În exemplul anterior funcția pară

f de x egal cu 2-a minus x la pătrat

Haideți să facem un mic tabel de

Valori avem x și f d x pentru x

egal cu unu obținem 2 minus unu

unu pentru x egal cu minus 1 avem

aceeași valoare 1 pentru că funcția

este pară pentru x egal cu 2 obținem

2 minus 4 minus 2 iar pentru x

egal cu minus doi avem minus 2

urmare graficul va conține aceste

puncte a de coordonate 1 1 b de

coordonate minus 1 1 c de coordonate

2 minus 2 și d de coordonate minus

2 și minus 2 noi încă nu știi să

reprezentați grafic Funcția de

gradul 2 Aceasta este o funcție

de gradul al doilea pentru că x

apare la puterea a doua beți învățam

mai târziu să reprezentați grafic

astfel de funcții Am vrut doar

să evidențiezi o proprietate importantă

a acestora Iată cum arată graficul

acestei funcții mănânc mai aici

punctul A de coordonate 1 1 Iată

Aici este punctul a b de coordonate

minus unu unu Aici este punctul

B C de coordonate 2 și minus 2

Aici este punctul c și d de coordonate

minus 2 minus 2 dacă ne uităm cu

atenție la acest grafic observăm

că el este Simetric în raport cu

Axa o y așa dar e bine să reținem

că În graficul unei funcții pare

este întotdeauna Simetric în raport

cu Axa o y să vedem acum ce se

întâmplă în cazul funcțiilor impare

pornind de la exemplul anterior

f de x egal cu x la a treia plus

x am văzut că aceasta este o funcție

impară pentru x egal cu unu obținem

f de x egal cu 1 la a treia plus

1 2 iar pentru x egal cu minus

unu obținem minus RDX adică în

minus 2 prin urmare graficul aceste

funcții va conține punctul A de

coordonate 1 și 2 și b de coordonate

minus 1 și minus 2 dar aceste te

sunt simetrice în raport cu originea

reperului cartezian Iată cum arată

graficul aceste funcții avem punctul

A de coordonate 1 2 Ia stai Ce

este punctul a b de coordonate

minus 1 minus 2 Am putea să mai

dăm și alte valori în să obținem

numere prea mari e suficient însă

să rețineți că graficul unei funcții

impare este întotdeauna simetrică

raport cu originea reperului cartezian

și e finală scurtă observație dacă

domeniul de definiție al unei funcții

nu este mulțime simetrică nu se

pune problema studierii parității

funcției Așadar să bem paritatea

numai atunci când domeniul este

o mulțime simetrică pe curând