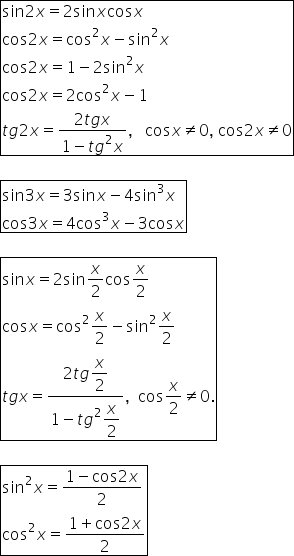Funcțiile trigonometrice pt. argumentul dublu și triplu

în această lecție vom demonstra

formulele trigonometrice ale argumentului

dublu și triplu dacă între o formulă

avem de exemplu sinus de x atunci

x este argument simplu dacă avem

sinus de 2x atunci vorbim de un

argument dublu iar dacă avem sinus

de 3x îmi spune că avem un argument

triplu în continuare ne propunem

să demonstrăm formulele pentru

argumentul dublu și triplu iar

pentru aceasta a vom aplica formulele

trigonometrice pentru suma a două

unghiuri pe care le am văzut în

lecțiile trecute Haideți să ne

reamintim cosinus de a plus b este

egal cu cozi de acord de b minus

sin de a sin de B sinus de a plus

b este egal cu SIM de acul de b

plus coș de asa in DB iar tangentă

de a plus b este tangentă de a

plus tangentă de b supra 1 minus

tangentă de a ori tangentă de b

o să deducem mai întâi formula

pentru sinus de 2x 2 x se poate

scrie ca o sumă ax plus x și aplicăm

a doua formulăm și vom avea ținuți

de x cosinus de x plus cosinus

de x ori sinus de x așadar am găsit

formula sinus de 2x egal cu 2 sin

de x coș de x aceasta este formula

pentru sinus ul argumentului dublu

Iată aici avem 2x dacă aplicăm

această formulă pentru argumentul

simplu Deci în loc de 2x vom scrie

x atunci în formulăm în loc de

x mom avea x supra 2 Așadar sinus

de x va fi egal cu 2 ori sinus

de x supra 2 ori cosinus de x supra

2 să vedem care e formula pentru

cosinus de 2x avem cosinus de x

plus x și aplicăm formula sumei

de mai sus obținem cosinus de x

cosinus de x minus sinus de x sinus

de x prin urmare obținem formula

cosinus de 2x egal cu coș pătrat

de x minus sin pătrat de x dar

coș pătrat de x conform formulei

fundamentale a trigonometriei este

1 minus sim pătrat de x minus sim

pătrat de x și obținem următoarea

formulă pentru cosinusul unghiului

dublu cos de 2x egal cu 1 minus

2 sim pătrat de x dar pornind de

la această formulă putem să exprimăm

și Simpa trei de x în funcție de

cosinus Deci cos de 2x este coș

pătrat de x minus iar în loc de

sim pătrat de x avem 1 minus coș

pătrat de x și obținem următoarea

formulă cosinus de 2x egal cu 2

coș pătrat de x minus 1 Așadar

Iată am găsit trei formule pentru

cosinus de 2x notez această formulă

cu 1 și 2 din Formula 1 putem Exprimați

în pătrat de x și obținem sim pătrat

de x egal cu 1 minus cosinus de

2x supra 2 iar din formula a doua

obținem cost pătrat de x egal cu

1 plus cosinus de 2x supra 2 este

bine să reținem și aceste formule

pentru că o să le aplicăm în exerciții

acum mai trebuie să exprimăm tangenta

unghiului dublu vom folosi această

formulă pentru tangenta sumei tangentă

de 2x este tangentă de x plus x

egal cu tangentă de x plus tangentă

de x supra 1 minus tangentă de

x ori tangentă de x și obținem

2 tangentă de x supra 1 minus tangentă

pătrată de x am găsit Așadar formula

tangentă de 2x egal cu 2 tangentă

de x supra 1 minus tangentă pătrată

de x dacă în locul argumentului

dublu avem un argument simplu atunci

formula de vin a tangentă de x

egal 2 ori tangentă de x supra

2 supra 1 minus tangentă pătrată

de x supra 2 deci argumentul în

acest caz se înjumătățește această

formulă este valabilă atâta timp

cât costă pneus de 2 x este diferit

de 0 deoarece tangenta este raportul

dintre sinus și cosinus și cosinus

de x diferit de 0 iar pentru a

doua formulă vom pune condiția

cosinus de x pe 2 să fie diferit

de 0 acesta a fost formulele trigonometrice

pentru argumentul dublu În continuare

ne propunem să calculăm sinus de

3x respectiv cosinus de 3x sinus

de 3x se poate scrie sinus de x

plus 2 x și acum aplică în formula

pentru suma a două unghiuri și

avem sinus de x ori cosinus de

2x plus cosinus de x ori sinus

de 2x egal cosinus de x pe lângă

în loc de cosinus de 2x Putem să

scriem 1 minus 2 Sin pătrat de

x am văzut mai devreme că are loc

această relație plus cosinus de

x iar în loc de sinus de 2x avem

2 sin de x coș de x egal desfacem

paranteza sin de x minus 2 sinus

la a treia de x plus 2 sinus de

x ori cosinus pătrat de x egal

cosinus de x minus 2 la a treia

de x plus 2 sin de x iar în loc

de cost pătrat de x Putem să scriem

1 minus sim pătrat de x conform

formulei fundamentale a trigonometriei

egal cu sin de x minus 2 sin la

a treia de x plus 2 sinus de x

minus 2 la a treia de x egal sinus

de x cu 2 c d x este 3 scene de

x iar minus 2 sinus la a treia

cu minus 2 sinus la a treia este

minus 4 țin la a treia de x am

găsit Așadar formula sinus de 3x

egal cu 3 sinus de x minus 4 la

3 de x în continuare 100 de duce

formula pentru cosinus de 3 x coș

de 3x este cosinus de x plus 2

x aplică formula pentru suma a

două unghiuri și obținem cos de

x coș de 2x minus sin de x sinus

de 2x egal coș de x în loc de cosinus

de 2x voi scrie 2 costă trei de

x minus unu vreau să scrie doar

în funcție de cosinus această relație

minus sinus de x ori în loc de

sinus de 2x avem 2 sin de x coș

de x egal cu 2 cos la a treia de

x minus coș de x minus 2 sim pătrat

de x ori coș de x o să scriu unui

coș de x pe lângă ținuți pătrat

de x puffy 1 minus costă trei de

X și Avem doi cost la a treia de

x minus coș de x minus 2 coș de

x plus 2 cos la a treia de x egal

2 cozi la a treia plus 2 costa

a treia este 4 cost la a treia

de x și minus 3 cosinus de x Deci

am găsit formula cosinus de 3 x

este egal cu 4 cosinus la a treia

de x minus 3 cosinus de x în cele

ce urmează vom exprimați sinus

și cosinus în funcție de tangentă

jumătății unui unghi iar aceste

formule mai poate denumirea de

substituție universală să recapitulăm

puțin formulele demonstrat a până

acum sinusul argumentului dublu

este egal cu 2 sin de x coș de

x pentru cosinusul argumentului

dublu avem trei formule pe care

le putem aplica cos de 2x este

costă trei de x minus sim pătrat

de x sau 1 minus 2 sim pătrat de

x sau 2 costă trei de x minus unu

iar tangenta unghiului dublu tangentă

de 2x este 2 tangentă de x supra

1 minus tangentă pătrată de x argumentul

simplu poate fi văzut ca dublul

unghiului pe jumătate prin urmare

din această relație obținem următoarea

formulă sinus de x este 2 sinus

de x pe 2 cozi de x pe 2 iar această

relație duce la următoarea formulă

Costi news de x este egal cu coș

pătrat de x pe 2 minus sim pătrat

de x pe 2 de asemenea avem tangentă

de x egal cu 2 tangentă de x pe

2 supra 1 minus tangentă pătrată

de x pe 2 am mai văzut și aceste

formule sim pătrat de x este egal

cu 1 minus cos de 2 x pe 2 iar

cost pătrat de x este 1 plus cosinus

de 2x supra 2 formulele pentru

argumentul triplam sunt următoarele

sinus de 3x este egal cu 3 sinus

de x minus 4 sinus la a treia de

x iar cosinus de 3 x este egal

cu 4 cost la a treia de x minus

3 coș de x în continuare ne propunem

să scriem sinus de x în funcție

de tangentă jumătății unui unghi

sinus de x se poate scrie sinus

de x pe 1 acum aplicăm această

formulăm în loc de sinus de x voi

scrie 2 sinus de x pe 2 ori cosinus

de x pe 2 iar 1 se poate scrie

sinus pătrat de x pe 2 plus coș

pătrat de x pe 2 suma dintre pătratul

sinusului și pătratul cosinusului

unui unghi este întotdeauna egală

cu unu în continuare o să împărțim

atât numărătorul cât și numitorul

la coș pătrat de x pe 2 deoarece

dorim ca în această formulă să

îmi apară tangentă de x pe 2 Dacă

împărțim numărătorul la coș pătrat

de x pe 2 se va simplifica acest

cosinus de x pe 2 și obținem 2

sinus de x pe 2 supra cosinus de

x pe 2 iar dacă împărțim numitorul

la coș pătrat de x pe 2 și scrie

ma apoi ca o sumă de două fracții

vom avea a coste pătrat de x pe

2 supra coș pătrat de x pe 2 se

simplifică și ne dă 1 plus iar

Aici îmi scrie sinus pătrat de

x pe 2 supra cosinus pătrat de

x pe 2 egal țin de x pe 2 supra

coș de x pe 2 este tangentă de

x pe 2 Iar acest raport sim pătrat

supra costă trat este tangentă

pătrată de x pe 2 Așadar obținem

2 tangentă de x pe 2 supra 1 plus

tangentă pătrată de x supra 2 Așadar

se reține formula sinus de x egal

cu 2 tangentă de x pe 2 supra 1

plus tangentă pătrată de x pe 2

în continuare o să demonstrăm formula

pentru cosinus de x în funcție

de tangență unghiului pe jumătate

cosinus de x este cosinus de x

pe 1 aplicăm această relație și

avem cos pătrat de x pe 2 minus

sim pătrat de x pe 2 iar în loc

de 1 o să scriem din nou simt pătrat

de x pe 2 plus coș pătrat de x

pe 2 o să împărțim atât numărătorul

cât și numitorul lacost pătrat

de x pe 2 și vom obține aici se

simplifică și ne dă 1 minus sim

pătrat de x pe 2 supra coș pătrat

de x pe 2 este tangentă pătrată

de x pe 2 sim pătrat de x pe 2

supra coș pătrat de x pe 2 este

tangentă pătrată de x pe 2 plus

1 așa dar am găsit formula cosinus

de x egal 1 minus tangentă pătrată

de x pe 2 supra 1 plus tangentă

pătrată de x pe 2 putem să adăugăm

și aceste două formule la cele

scrise anterior Deci sinus de x

este 2 tangentă de x pe 2 supra

1 plus tangentă pătrată de x pe

2 iar cosinus de x este 1 minus

tangentă pătrată de x pe 2 supra

1 plus tangentă pătrată de x pe

2