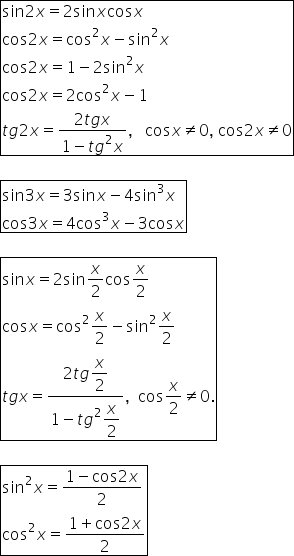Funcțiile trigonometrice pt. argumentul dublu și triplu (aplicații)
Tag-uri
Partajeaza in Google Classroom

Transcript
în acest clip o să rezolv trei
exerciții în care voi aplica formulele
argumentului dublu primul exercițiu
se dă cosinus de x egal cu minus
2 supra 3 unde x aparține intervalului
pi supra 2 pi se cere să calculăm
sinus de 2x cosinus de 2x tangentă
de 2x sinus de 4x și cosinus de
4 x pentru a calculați sinus de
2x Trebuie mai întâi să calculăm
sinus de x unghiul x este în cadranul
al doilea prin urmare sinusul va
fi pozitiv sinus de x este radical
din 1 minus coș pătrat de x și
avem radical din 1 minus 4 pe 9
și obținem radical din 5 pe 3 Acum
putem să calculăm sinus de 2x acesta
va fi egal cu 2 sinus de x cosinus
de x egal cu 2 ori radical din
5 supra trei ori minus 2 pe 3 și
egal cu minus 4 radical din 5 supra
9 cosinus de 2x este Haideți aplicăm
această formulă 1 minus 2 sim pătrat
de x și avem 1 minus 2 ori sinus
de x este radical din 5 pe 3 de
sinus la pătrat este 5 pe 9 egal
cu 9 minus 10 minus 1 pe 9 tangentă
de 2x putem fi să aplicăm această
formulăm dar în acest caz Trebuie
mai întâi să calculăm tangentă
de x sau altă variantă este să
scriem tangentă de 2x ca raportul
dintre sinus de 2x și cosinus de
2x pe care deja le am calculat
sinus de 2x este minus 4 radical
din 5 supra 9 iar coș de 2x este
minus 1 pe 9 se simplifică nouă
și obținem 4 radical din 5 pentru
a calculați sinus de 4x Putem să
scriem 4x ca produsul dintre 2
ori 2 x și aplicăm prima formulăm
avea 2 ori sinus de 2x ori cosinus
de 2x egal cu 2 ori sin de 2x este
minus 4 radical din 5 pe 9 iar
cosinus de 2x este minus 1 pe 9
egal cu 8 radical din 5 supra 81
cosinus de 4 x este egal cu cosinus
din doi ori doi x egal cu 1 minus
2 Sin pătrat de 2x și egal cu 1
minus 2 ori sinus de 2x este minus
4 radical din 5 pe 9 ridicăm la
pătrat și obținem 16 ori 5 supra
81 egal 81 minus 160 supra 81 și
egal cu minus 79 supra 81 al doilea
exercițiu se dă sinus de x egal
cu 1 supra 3 unde x aparține intervalului
0 pi supra 2 și se cere tangentă
de 2x tangentă de 2x este egal
cu 2 tangentă de x supra 1 minus
tangentă pătrată de x trebuie Așadar
să calculăm mai întâi tangentă
de x tangentă este raportul dintre
sinus și cosinus așa dar va trebui
mai întâi să calculăm cosinus de
x x este un număr din cadranul
întâi din intervalul 0 pi supra
2 prin urmare cosinus de x va fi
pozitiv cosinus de x y este radical
din 1 minus simt pătrat de x adică
radical din 1 minus 1 pe 9 9 minus
1 este 8 radical din 8 este 2 radical
din 2 supra 3 și acum putem calcula
tangentă de x avem sinus de x supra
fost sinus de x egal sinus de x
este 1 pe 3 iar cozi de x este
2 radical din 2 supra 3 se simplifică
30 și obținem 1 supra 2 radical
din 2 raționalizăm și obținem radical
din 2 supra 4 și acum tangentă
de 2x va fi 2 ori tangentă de x
radical din 2 pe 4 supra 1 minus
tangentă pătrată dacă ridicăm această
fracție la pătrat obținem 2 pe
16 se simplifică și ne rămâne unul
pe 8 Lidl aici simplifica cu două
și a veni radical din 2 pe 2 8
minus 1 7 pe 8 egal cu radical
din 2 pe 2 ori 8 supra 7 egal cu
4 radical din 2 pe 7 și ultimul
exercițiu se dă sinus de x egal
cu 4 pe 5 x aparține intervalului
pi supra 2 pi se cere să calculăm
sinus de x supra doi această formulă
punând în locul argumentului x
x supra 2 iar în loc de cosinus
de 2x vom avea cosinus de x aplicăm
Așadar formula sinus pătrat de
x pe 2 este 1 minus cosinus de
x totul supra doi va trebui mai
întâi să calculăm cosinus de x
x este un unghi din cadranul al
doilea din intervalul pi supra
2 pi și atunci cosinus de x va
fi negativ Deci cosinus de x este
minus radical din 1 minus simt
pătrat de x egal cu minus radical
din 1 minus sinus la pătrat este
16 pe 25 sub radical efectuăm scăderea
vom avea 25 minus 16 nouă pe 25
extrage radicalul și ne rămâne
3 pe 5 Deci sinus la pătrat de
x supra 2 este 1 minus coș de x
adică minus 3 pe 5 plus 3 supra
5 totul supra 2 egal 8 supra 5
supra 2 egal cu 8 supra 10 se simplifică
și de rămâne 4 pe 5 acum trebuie
să vedem semnul funcției sinus
dacă x este un unghi din cadranul
al doilea pi supra 2 pi atunci
x supra 2 o să aparține intervalului
pi supra 4 pi supra 2 Deci un duel
x supra 2 va fi un unghi în cadranul
întâi în primul cadran sinusul
este pozitiv Așadar sinus de x
supra 2 este mai mare ca 0 Revenim
la această relație și obținem sinus
de x supra 2 egal cu plus radical
din 4 pe 5 adică 2 supra radical
din 5