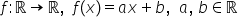Graficul unei funcții liniare

să vedem acum Ce este o funcție

liniară și cum trasăm graficul

unei asemenea funcții și avem exemplul

funcția f definită pe r cu valori

in r f de x egal cu x plus 2 cum

trasăm graficul unei asemenea funcții

având în vedere că Iată aici domeniul

de definiție este infinit Este

o mulțime infinită dacă domeniul

de definiție era mulțime finită

în tabel trebuia să trecem toate

valorile care erau în acel domeniu

Însă acum fiind vorba de o mulțime

infinită nu putem să scriem toate

numerele reale Cum să putem să

trecem câteva dintre ele și Haideți

să facem acest lucru facem tabelul

și vom trece câteva valori pe care

ni le dorim să fie ușor de calculat

aici avem x și fdx și putem să

luăm de exemplu x egal cu minus

2 minus 1 chiar să dea alegem cu

cu timp 0 1 și 2 cât este acum

e f de minus 2 f de x este x plus

2 f de minus 2 Nevada minus 2 adunat

cu 2 adică 0 și trecem aici 0-iv

mai departe de minus 1 este minus

1 plus 2 adică ne dă 1 f de 0 este

0 adunat cu doi Deci doi venim

și trecem aici 2 f de 1 Nevada

1 plus 2 adică trei și în final

fd2 înseamnă doi plus doi adică

patru Ce puncte am obținut Păi

avem perechile minus doi zero și

chiar o să le scriem aici minus

doi zero următoarea pereche minus

unu unu apoi Zero doi unu trei

și doi patru e bine și aceste puncte

Haideți acum să le Reprezentăm

în tu un sistem de coordonate și

avem aici axa o x axa ordonatelor

Deci avem o aici avem o x să ne

alegem unitatea de măsură acest

segment lungimea acestui segment

primul punct abscisă minus 2 ordonată

0 Deci avem aici minus 1 minus

2 fiind ordonanta zero înseamnă

că punctul se află pe axa o x 10

la Vama aici minus 1 1 3 c minus

1 pe o x 1 p y și iată punctul

iar d este cel de aici dar să îl

colorăm tot așa 0 și Doi Degeaba

un punct pe axa o y y avem aici

numărul 2 și punctul este acesta

urmează următorul punct abscisă

1 ordonată 3 avem aici noi chiar

avem aici 1 și ordonata este 3

și găsim și punctul Iată vorbim

de acest punct și ultimul punct

2 și 4 avem aici numărul 2 abscisă

2 ordonata 4 să găsim și următorul

punct adică este acesta dar Ce

observăm Cum sunt aceste puncte

e ușor de văzut de fapt toate aceste

puncte sunt coliniare chiar mai

mult dacă am luat și un alt punct

să spunem că îl iau pe 1 Da 1 atunci

dacă trecem aici 1 avem nevoie de

f de 1 care înseamnă 1 plus 2 ne

dă cu alte cuvinte 3 Deci vom avea

aici 3 și construind și acest punct

o să vedem că tot așa obținem tot

puncte coliniare de fapt orice

valoare amenda variabilei x punctele

care se vor obține vor fi coliniare

Ia să mai luăm un punct aici vom

obține acest punct apoi încă unu

încă unu și așa mai departe cu

alte cuvinte ce va fi graficul

acestei funcții de fapt se obține

o dreaptă și Haideți chiar să o

tras bun acesta este această dreaptă

este de fapt reprezentarea geometrică

a graficului funcției f ce avem

aici este de fapt o funcție liniară

și ide să notăm că o funcție care

este definită pe mulțimea numerelor

reale cu valori în mulțimea numerelor

reale iar legea de corespondență

are această formă a ori x plus

b unde a și b sunt numere reale

atunci o asemenea funcție se numește

funcție liniară și întotdeauna

graficul unei funcții liniare este

o dreaptă deci putem să spunem

că reprezentarea geometrică este

o dreaptă și atâta aici în acest

exemplu noi avem o asemenea a funcției

Ea este definită pe r cu valori

inel ca și aici Atenție nu contează

denumirea funcției putem să folosim

orice literă vrem iar legea de

corespondență are întradevăr această

formă pentru că aici putem să notăm

1 înmulțit cu x plus 2 cu alte

cuvinte a este 1 iar b este 2 Deci

avem aici b Și aici este A deci

întradevăr aici avem o functie

liniară Păi nu am demonstrat aici

riguros că de fapt graficul aceste

funcții este o dreaptă ce am dat

mai multe explicații intuitivă

poate că întru altă secvență video

să demonstrăm că întradevăr o funcție

liniară se reprezintă geometric

printre o dreaptă însă până atunci

haide să mai facem un exemplu și

avem funcția G definită pe r cu

valori in r g de x egal cu minus

2 ori x plus unu Este aceasta o

funcție liniară pe domeniul de

definiție terca și codomeniul Deci

avem îndeplinită această condiție

însă să vedem dacă legea de corespondență

are această formă adică a ori x

plus B pe ușor de văzut că a este

minus 2 iar b este un Prin urmare

avem o funcție liniară asta înseamnă

că deja știu reprezentarea geometrică

a graficului este o dreaptă atunci

dacă știm deja că vom obține o

dreaptă de câte puncte avem nevoie

pentru AO determina dacă avem un

singur printr un punct trec o infinitate

de drepte dar dacă avem două puncte

două puncte determină o dreaptă

și numai una Deci avem nevoie doar

de două puncte ca să găsim dreapta

și să Reprezentăm să facem tabelul

de Valori avem x g de x ce valori

să luăm oricare două numere reale

dorim de exemplu 0 și dacă x este

0 Calculați 0 avem minus doi ori

x adică minus 2 înmulțit cu 0 plus

1 cine de 1 și dacă x este 1 g

D1 va fi minus doi ori unu plus

unu Deci ne dă minus 2 plus 1 minus

1 și să notăm punctele avem 0 și

minus unu prima pereche pardon

zero și unu și a doua unu și minus

1 pe prezentăm sistemul de coordonate

buhn alegem unitatea de măsură

avem aici unitate de și avem punctul

de coordonate 0 și 1 b c avem 0

pe axa o x 1 pe axa o asta înseamnă

că punctul nostru se află aici

chiar Haideți să notăm avem aici

A mare și aici de mare Deci aici

vom trece punctul A mare și avem

unu și minus unu Deci abscisă 1

să trecem 1 ordonată minus 1 și

am obținut iartă acest punct și

avem aici punctul b mare graficul

funcției este dreapta care trece

prin aceste două puncte Deci reprezentarea

geometrică a graficului funcției

G este această dreaptă dreapta

AB aș vrea acum să mai facem un

ultim exemplu și avem funcția definită

pe r cu valori în er hdt este egal

cu 3 este o funcție liniară Păi

trebuie să verificăm dacă legea

de corespondență are această formă

adică a înmulțit cu variabila care

este te aici adunat cu un alt număr

real în stau aici observăm că nu

ne apare variabila de asta înseamnă

că nu avem o funcție liniară iată

că de fapt dacă trecem pe 3 chiar

o să îl mutăm ca să ne fie mai

ușor de urmărit aici e ușor de

sesizat că a este de fapt 0 din

această cauză nu apare aici variabila

te avem 08 adunat cu 3 a este 0

b este 3 Cu alte cuvinte avem tot

așa o funcție liniară dacă e o

funcție liniară înseamnă că reprezentarea

geometrică a graficului va fi o

dreaptă să facem tabelul de Valori

și un tabel foarte simplu avem

aici te și hdd dar orice valoare

ia da lui te întotdeauna HD valoarea

respectivă o să fie trei dacă luăm

de exemplu 1 o să avem trei dacă

luăm 4 o să ne dea tot trei dacă

luăm 2015 o să obținem HD 2015

tot trei și acum haide să Reprezentăm

de fapt mai întâi să trecem punctele

a de coordonate 1 și 3 iar b de

coordonate 4 și 3 alege aceste

două puncte axa o x axa o y Cum

treci imediat și unitatea de măsură

primul punct avem abscisă 1 ordonată

3 Deci avem aici 1 aici avem 1

2 și 3 bun și vom obține primul

punct punctul A mare punctul b

mare avem abscisă 4 Deci 2 3 4

iar ordonata este tot trei și gata

Aici este punctul b mare unim cele

două puncte și ceea ce vom obține

va fi reprezentarea geometrică

a graficului funcției de fapt avem

o dreaptă care este paralelă cu

Axa o x și mai merită să menționăm

aici că o asemenea f este numește

funcție constantă de ce se numește

așa pentru că o asemenea funcție

nu își modifică valoarea oricare

ar fi valoarea variabilei