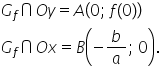Graficul unei funcții liniare (Intersecția cu axele de coordonate)

când lasam graficul unei funcții

liniare uneori e mai folositor

să găsim acele puncte care se află

la intersecția dintre grafic și

axele de coordonate pentru că noi

știm graficul unei funcții liniare

Ce este este o dreaptă Deci dacă

avem un sistem de coordonate avem

aici o x Aici este axa ordonatelor

o y un graficul unei funcții liniare

am spus că este o dreaptă Păi dacă

este o dreaptă atunci iar va intersecta

cel puțin una din cele două axe

de coordonate ia poate să arate

de exemplu astfel și a ta avem

intersecția dintre grafic și axa

o x aici iar intersecția dintre

grafic și axa o y este dată de

acest punct sau putem să avem graficul

funcției să arate așa și cum de

intersecție dintre graficele de

coordonate sunt acesta și acesta

sau mai putem să avem și varianta

în care funcția liniară este o

funcție constantă și atunci În

graficul a va fi O dreaptă paralelă

cu Axa o x și uite o putem desena

chiar aici acum în această situație

numai intersectează axa o x în

se intersectează axa o y o intersectează

în acest punct Deci ideea este

că oricum ar arăta graficul acelei

funcții liniare el va intersecta

fie ambele ax fie axa o y De ce

Mereu vom avea cel puțin un punct

care se află și pe graficul funcției

și pe una din cele două axe și

acum Haideți să luăm un exemplu

Și luăm funcția f definită pe r

cu valori in r f de x egal cu 2x

minus 3 vrem să tras în graficul

aceste funcții găsim chiar punctele

de intersecție ale graficului cu

axele de coordonate am văzut graficul

e o dreaptă că avem aici o funcție

liniară prin urmare va intersecta

fie ambele axa fie doar axa o y

Oricum ar fi avem cel puțin un

punct de intersecție Cum arată

însă coordonatele acestor puncte

Dacă dreapta care Reprezintă graficul

funcției ar fi de această formă

cum am desenat aici și punctele

de intersecție sunt acesta și acesta

care e forma cordonate lor acestui

punct p este pe axa o x asta înseamnă

că ordonata este 0 Deci dacă abscisa

este să îi spunem a ordonanta va

fi 0 acest punct însă are abscisa

0 pentru că el se află pe o y iar

ordonata să îi spunem b Asta e

forma punctelor pe care le căutăm

și atunci Haide să trasăm tabelul

de Valori avem aici x și fdx ca

să găsim acest punct ce condiție

trebuie să trecem pentru x Păi

fiind un punct pe o y a știi să

ne apărat trebuie să fie 0 deci

de mai întâi lui x valoarea zero

trecem aici x egal cu 0 și calculăm

f de 0 avem aici 2 ori 0 minus

3 ne dă minus trei și venim și

trecem aici minus trei și ce am

găsit pe acest punct de coordonate

0 și minus 3 aparține graficului

funcției f care aparține și axa

o y Deci se află la intersecția

dintre graficul funcției și axa

o y pentru al doilea punct cel

care se află pe axa o x trebuie

să trecem ce condiție Păi ordonata

trebuie să fie 0 Deci trebuie să

vedem pentru ce valoare a lui x

e f de valoarea respectivă ne dă

0 și atunci ai de să calculăm când

e f de x este 0 pe acest lucru

se întâmplă dacă și numai dacă

este x este 2x minus 3 De ce este

echivalent cu 2x minus 3 egal cu

0 echivalent mai departe cu x egal

cu 3 supra 2 alte cuvinte e f de

x este 0 numai dacă dacă și numai

dacă x este 3 supra 2 venim aici

și ștergem semnul întrebării trecem

3 supra 2 și am găsit următorul

punct Iată are coordonatele 3 supra

doi și zero el se află și pe graficul

funcției De ce aparține graficului

funcției intersectat cu Axa o x

pentru că așa arată un punct care

se află pe axa absciselor și să

trasăm acum graficul Deci vom trece

aceste două puncte și Avem așa

primul punct și să 0 ordonată minus

3 Haideți să ne luăm și o unitate

de măsură lui tataie să trecem

unitate de măsură și Avem așa 0

minus 3 Deci trecem minus 3 pe

axa o y minus 1 minus 2 minus 3

Aici este punctul nostru de coordonate

0 și minus 3 și următorul punct

are abscisă 3 supra 2 și ordonata

0 Deci aici este 1 de fapt mamai

la stânga Aici este unul aici este

2 înseamnă că la jumătatea distanței

este 3 supra 2 și punctul nostru

este aici de coordonate 3 supra

2 0 1 m cele două puncte chiar

să facem tot cu alb și ce am obținut

Aici este graficul funcției f de

x pe care îl am trasat folosind

intersecția dintre grafic și axele

de coordonate aceste două puncte

sunt punctele de intersecție deci

nu e nimic complicat Trebuie mai

întâi să îi dăm lui x valoarea

0 Da și apoi calculăm Cât este

e f de 0 iar apoi îi dăm lui fdx

valoarea 0 și vedem pentru ce valoare

a lui x întradevăr f de valoarea

respectivă ne dă 0 De ce uneori

e mai folositor să trasăm gras

unei funcții liniare chiar prin

punctele de intersecție cu axele

cum am făcut aici pentru că e posibil

ca în anumite exerciții Să ni se

ceară să determinăm aria triunghiului

format de graficul funcției cu

axele de coordonate adică ne referim

la aria acestui triunghi și atunci

avem nevoie chiar de coordonatele

punctelor care reprezintă vârfurile

triunghiului Ai citit deja că avem

coordonatele 0 și 0 însă avem nevoie

să le știm și pe acestea două și

atunci folosim intersecție a graficului

cu axele de coordonate Ce fel de

triunghi avem aici pe este un triunghi

dreptunghic avem aici un unghi

cu măsura de 90 de grade și atunci

Haide să scriem formula să mutăm

ce am scris aici Cu cât este egala

aria unui triunghi dreptunghic

mai întâi Haideți să notăm și punctele

avem aici punctul A mare aici și

b mare Deci ei are coordonatele

3 pe 2 și 0 acesta este a iar acesta

este b și acum haide să scriem

formula ariei pentru un triunghi

dreptunghic aria triunghiului a

o b este egală cu semi produsul

lungimilor catetelor de cea bem

aici supra 2 iar aici Care sunt

catetele a și o b de ce avem produsul

a ori o b aici avem lungimile celor

două catete Ce lungime are această

catetă notată o A păi Câte unități

de măsură avem aici de la originea

axei o x până în acest punct avem

3 supra 2 unități 3 pe 2 unități

de măsură însă aici Câte unități

de măsură avem atenție deși aici

avem ordonata minus trei noi vrem

să găsim lungimea acestei catete

Deci ne interesează Câte unități

de măsură avem nu ne deranjează

faptul că aici avem un număr negativ

pentru că de fapt aici avem trei

unități de măsură și atunci Haide

să calculăm vom avea așa linie

de fracție numitorul 2 AO este

3 supra 2 iar o b este 3 și vom

avea 3 supra 2 ori 3 o să ne dea

nouă nouă supra 2 totul supra 2

avem o fracție supra puse aici

linia principală de fracție și

cum obține de fapt în 9 pe patru

chiar o să șterg aici că nu mai

am mult spațiu și o să scriu direct

9 supra aceasta este aria triunghiului

format de graficul funcției cu

axele de coordonate un alt exemplu

este acesta în care avem funcția

G definită pe r cu valori in r

g de x egal cu x plus 4 și vrem

să trasăm graficul funcției folosind

Intersecția cu axele de coordonate

în tabelul de Valori si vom trece

avem aici x GTX mai întâi îi dăm

lui x valoarea zero și apoi calculăm

valoarea funcției G în 0 iar apoi

vedem pentru ce valoare a lui x

g de valoarea respectivă în a de

0 de 0 mai întâi Cât este de dacă

x este 0 Calculați Jet 0 avem 0

plus 4 adică ne dă patru trecem

aici și avem acest punct de coordonate

0 și 4 care se află pe graficul

funcției g și unde se mai află

Păi având abscisă Acer înseamnă

că el se află pe axa o y Deci la

intersecția dintre graficul funcției

cu Axa o y acum dacă g de x ne

dă 0 Deci dacă g de x este 0 este

1 6 lași lucru cu a spune că x

plus patru pentru că atât Este

g de x x plus patru este 0 echivalent

cu x egal minus 4 Deci pentru x

egal minus 4 g de minus 4 ne dă

0 e clar aici avem o relație echivalentă

Deci dacă x minus 4 rezultă că

g de minus 4 estero și avem punctul

coordonatele Pardon minus 4 și

0 minus 4 și 0 aparține graficului

funcției G intersectat cu ce axa

Păi ordonata e 0 de cel se află

pe axa o x și să trasăm aceste

două puncte avem 0:04 Deci pe o

y se 4 avem 1 2 3 Aici este 4 și

a avem acest punct pe care Haide

să notăm cu A mare avem aici punctul

A mare și minus 45 0 Deci venim

și trecem aici minus 4 minus 1

minus 2 minus 3 minus 4 este aici

vom trece punctul b mare Deci trecem

aici b mare unim cele două puncte

și ce am obținut Aici este graficul

funcției G pe care îl am de terminat

la am trasat folosind Intersecția

cu axele de coordonate De ce reținem

Că îi dă mai întâi lui x valoarea

0 iar apoi îi dăm și lui gdx valoarea

0 și astfel determinăm punctele

care se află pe axele de coordonate

Dar și pe graficul funcției