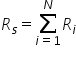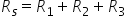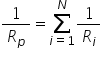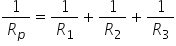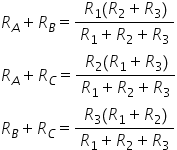Grupările de rezistoare serie, paralel, stea şi triunghi.

în cea de a șaptea Lecție despre

curentul electric continuu vom

discuta despre Gruparea rezistoarelor

atât grupările în serie și paralel

cât și cu grupurile mai complexe

precum stea și triunghi Gruparea

rezistoarelor este de două tipuri

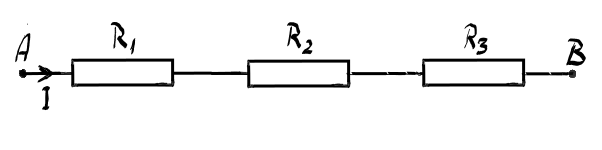
și anume Gruparea în serie când

rezistoarele au același curent

trecând prin ele precum în această

imagine Deci avem trei rezistoare

R1 r2 și ar3 și curentul ce trece

prin ele va fi același dorim să

găsim o rezistență echivalentă

în serie care poate înlocui această

grupare de rezistoare în același

circuit adică între aceleași puncte

a și b având aceeași diferență

de potențial căciula și curent

trecând prin rezistor observăm

că putem scrie diferența de potențial

sau tensiunea dintre punctele o

a b în felul următor alegem de

numim două puncte intermediare

c și d și observăm că o a b care

prin definiție este potențialul

din punctul A minus valoarea potențială

din punctul b se poate scrie ca

va minus b c plus b c minus v d

plus v d minus vb dar mai departe

observăm că a minus b c este potențial

diferența de potențial sau tensiunea

de pe primul rezistor De ce aceasta

este u1 la fel v c minus vedem

este diferența de potențial de

la bornele rezistorului 2 De ce

este tensiunea cu 2 și în final

v d minus v b este diferența de

potențial de la bornele rezistorului

3 De ce este u3 egalitate intermediară

este evidentă pentru că toți termenii

toate potențialele intermediare

se simplifică deci putem vedea

că v c minus WC plus vc 0 și la

fel minus vd plus b d este 0 Deci

obținute A minus bebe în concluzie

putem scrie că tensiunea totală

Care este o a b este egal cu suma

tensiunilor de la bornele fiecărui

rezistor unu plus doi plus trei

dar tensiunea totală este rezistența

echivalentă muncită curentul e

Deci vă reamintesc căutăm un r

s astfel încât o a b și e să fie

același Deci va fi RS ori iar 1va

Fier 1 ori cu 2 Fier 2 ori și așa

mai departe simplificând curentul

e Care este comun în Gruparea în

serie obținem ecuația pentru rezistența

echivalentă în Gruparea în serie

Care este suma rezistențelor individuale

dacă rezistențele sunt egale atunci

rezistența echivalentă în serie

va fi numărul de rezistente rezistente

înmulțită cu rezistența individuală

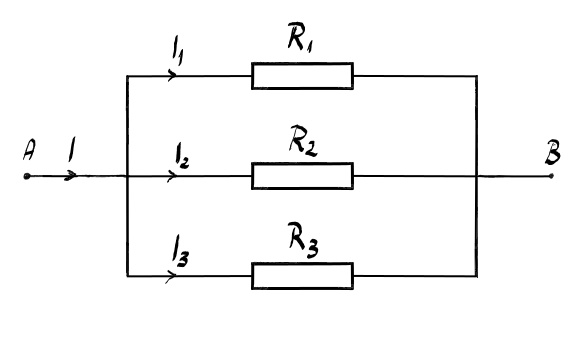
Sila doilea tip de grupare este

în paralel Gruparea rezistoarelor

în paralel are loc atunci când

ele au aceeași tensiune și nu curent

la borne vedem acest tip de grupare

în această schemă de ce avem trei

rezistențe sau rezistoare mai precis

R1 r2 r3 ele având aceleași tensiune

unul fiind cu ape cu doi fiind

tot o b și u trei fiind din nou

OB la fel Încercăm să găsim o rezistență

echivalentă pe care o notăm cu

r p astfel încât diferența de potențial

sau tensiunea dintre punctele a

și b să fie aceeași iar curentul

e să fie și el aceeași curentul

total ce avem în curent pentru

rp și avem același curent e total

Gruparea de rezistoare vom avea

bineînțeles curent notați cu a

1 2 și 3 pe fiecare ramura din

prima lege kirchhoff pentru nodul

a putem vedea imediat că e este

egal cu 1 plus 2 plus și tăi și

pornind de la această ecuație de

ce este egal cu 1 plus 2 plus 3

în acest caz dar din schema sau

circuitul echivalente putem scrie

că e este egal cu AB adică împărțit

la rezistența echivalentă în paralel

și la fel și unul va fi împărțit

la unu e doi va fi uab împărțit

la r 2 și 3 o a b împărțit la a

3 în concluzie Putem să scriem

că inversul rezistenței echivalente

în paralel este egal cu suma inverselor

rezistențelor individual dacă acestea

sunt egale obținem că rezistența

echivalentă a grupării în paralel

va fi rezistența individuală împărțită

la numărul de astfel de rezistente

Wall not timp de grupare a rezistențelor

sau de grupări a rezistențelor

sunt așa numitele rezistenți în

stea și întruparea rezistențelor

în triunghi se referă la formă

geometrică și ea este aceea de

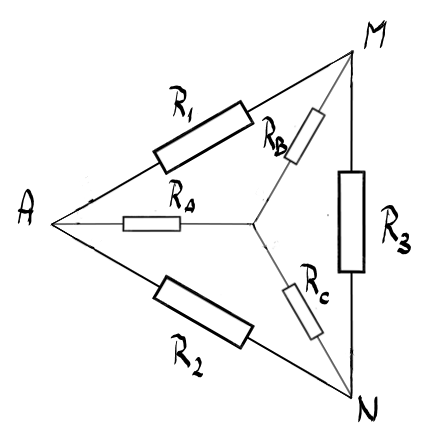
triunghi după cum vedem în culoarea

albastru deschis de ce rezistențele

R1 r2 r3 sunt grupate în triunghi

în această în acest rețea electrică

aceste grupare în triunghi arun

ar tăia 3 este apoi cu plată la

alta rezistențe L4 și L5 putem

calcula rezistența echivalentă

R ab Aplicând legile lui kirchhoff

câteodată în schimb este foarte

util adică mai rapid și mai eficient

calculul Dacă transformăm spre

exemplu această grupare în triunghi

din nou în albastru deschis întruna

în stea o grupare în stea este

cea în culoarea roșie Deci Gruparea

rezistențelor r a r b și r c din

această rețea se va numi o grupare

în stea pentru motive evidente

Haideți să vedem cum se calculează

rezistența între echivalentă dintre

punctele a și b folosind o transformare

triunghi stea Păi foarte simplu

relația de la care plecăm pentru

a rezolva acest caz este aceea

Că rezistența totală echivalentă

între punctele a m în Gruparea

triunghi trebuie să fie egală cu

rezistența între acelea de aer

în Gruparea stea la fel rezistența

între punctele A și n în Gruparea

triunghi trebuie să fie egală cu

rezistența între același punct

a a n în Gruparea stea Și în fine

că rezistența dintre punctele m

și n între în Gruparea triunghi

trebuie să fie egală cu rezistența

intre m și n în Gruparea stea în

felul acesta vedem că dacă rezistențele

în cele două grupări între a m

a n și m n sunt egale atunci Bineînțeles

că cele două grupări de rezistoare

cea triunghi în albastru deschis

și cea stea în roșu vor fi echivalent

Haideți să vedem ce înseamnă pentru

a calcula rezistența în Gruparea

triunghi între punctele a și m

vedem că putem să ajungem există

două grupări există Gruparea r1ko

singură rezistență și apoi grupare

a cu două rezistențe r2 și r3 între

punctele a și m deci între punctele

a și a mic ce stă o grupare în

paralel între R1 pe de o parte

și L2 și L3 pe de cealaltă parte

folosind relația pentru Gruparea

în paralel putem spune că 1 împărțit

la r a m triunghi va fi egal cu

1 pe R1 plus 1 pe r 2 plus r-3

Asta înseamnă din nou că între

punctele a și m r 1 și el o parte

și r2 și r3 pe de cealaltă parte

sunt în paralel iar r2 și r3 sunt

în serii Deci asta înseamnă această

ecuație deci de aici putem scrie

că e r a m în Gruparea triunghi

este egal cu 1 pe lângă r2 Plus

r3 împărțit la 1 plus r2 plus r

3 placi iar r a m în grupa reacțiuni

trebuie să fie egal cu RMN Gruparea

stea dar r a m în Gruparea stea

este aer apela sârbe deci putem

scrie mai departe că acesta este

egal cu a plus R B astfel avem

o prima relație care leagă rezistențele

stea a și b de rezistențele triunghi

unu doi trei la fel între punctele

A și n din motive identice putem

scrie același set de ecuații iar

a n triunghi este egal cu 1 supra

2 plus 1 supra R1 plus r3 din nou

ca să explicăm pentru a ajunge

de la a la aceste două puncte Avem

două laturi două trasee 1 cel direct

care trece pe rezistență r2 celălalt

care trece prin aer unul și apoi

r3 Deci r2 este în paralel cu Gruparea

serie R13 Gruparea serie are rezistența

echivalentă R1 plus ar3 Deci o

grupare în serie alugar unul cu

aer 3 va rezultatul rezistenței

echivalente 1 plus 3 iar această

grupare R1 plus 3 se află în paralel

cu r 2 în raport cu punctele A

și N și Deci rezistența totală

echivalentă între punctele A și

n va fi in versuri va fi unu pe

doi plus unu pe aer unu plus trei

deci r a n triunghi va fi egal

cu r 2 pe lângă 1 plus 3 împărțit

la 1 plus 2 plus 3 iar acesta va

fi egal cu rezistența echivalentă

în stea între a și n Deci va fi

egal cu a plus c of mor doilea

set de ecuații și mod Evident fără

a mai fi Cum din cer de A3 egalitate

Aplicând același acela mint pentru

punctele m și n Cum îmi ține că

RMN triunghi va fi egal cu r3 pe

lângă R1 plus Air 2 împărțit la

1 plus 2 plus 3 Care este egal

cu rezistența MN astea care este

r b plus r c aceasta este cerea

treia Ce datorii la stat de ecuații

Deci avem trei ecuații cu 3 necunoscute

r a r b r c și din această din

acest set de un sistem de 3 ecuații

cu 3 necunoscute se află r a r

b și f c și apoi în final putem

calcula rezistența dintre a și

b dar de data aceasta Folosind

valorile pentru rezistențele în

stea de ce eliminăm rezistența

în triunghi rezistențele în triunghi

și obținem pentru cele astea că

iar ab Care este format din rezistența

aia în serie cu restul de cinste

a plus rezistența echivalentă să

numim punctul acesta Cu ce cu o

deci rezistența echivalentă dintre

o și b iar rezist ne uităm de la

schimb la rețea la circuit observăm

că între o și b avem rezistențele

râde și iar patru în serie RC share

patru tot în serie iar acestei

grupări sunt în paralel între ele

Deci putem scrie că 1 p r o b este

egal cu 1 pe r b plus r4 plus 1

pe r c plus r50 din nou b și patru

sunt Evident în serie și cinci

sunt evidență în serie Deci rezistențelor

echivalente sunt sumele iar cele

două restant echivalente sunt în

paralel între punctele o și b Deci

avem această relație și în concluzie

putem scrie că ab este egal cu

a plus b plus r4 înmulțit cu RC

Plus r5 împărțit la r b plus RC

plus r4 plus R 5 și în felul acesta

am aflat rezistența echivalentă

dintre punctele a și b dar nu am

folosit relațiile sau legile chircov

și am folosit relația dintre grupările

stea și triunghi