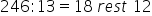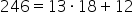Împărțirea cu rest a numerelor naturale
Tag-uri
Partajeaza in Google Classroom

Transcript
să vedem acum Ce înseamnă împărțirea
cu rest a numerelor naturale și
vom porni cu un exemplu avem aceste
7.000 și vrem să le distribuim
în mod egal În trei cutii putem
să facem acest lucru Păi Haideți
să începem distribuirea pune o
minge aici în a doua cutie punem
această minge în a treia punem
aceasta minge câte mingi mai avem
Păi mai avem aceste patru mingi
cum avem mai multe mingi rămase
decât numărul de cutii înseamnă
că putem să continuăm distribuirea
lor Deci în prima cutie trecem
și această minge aici o adăugăm
pe aceasta și mai punem o minge
și în cea de a treia Ce observăm
Pa iată că nu a mai rămas o minge
de ce nu am mai rămas o minge ca
rest pentru că această împărțire
7 împărțit la 3:00 nu este o împărțire
exactă este o împărțire cu rest
diferit de 0 care e restul restul
este 1 în a rămas aici o minge
Haideți să facem și împărțirea
facem Cum am învățat până acum
7 împărțit la 3 Păi 3 Se cuprinde
în 7 de două ori Deci avem 2 2
ori 3 ne dă 6 7 minus șase unu
mai avem Ce cifră să coborâm de
la deîmpărțit nu e cea mulți Nu
tai ci se numește restul acestei
împărțiri Deci avem 7 împărțit
la 3 este egal cu 2 rest 1 și acum
haide să scriem și denumirile 7
este deîmpărțitul știam deja notăm
cu d mare de la deîmpărțit 3 este
împărțitorul voi nota cu U mare
2 este câtul dar deja știam iar
restul este nu te mai chiar mare
de la rast Haide să vedem acum
cum putem să le exprimăm pe 7 pe
baza acestei împărțiri păi avem
așa șapte Deci 7 Cu cât este egal
Păi am văzut că el este egal cu
6 plus 1 bondar 6 este 3 ori 2
Deci avem 3 înmulțit cu 2 plus
1 de fapt ce am obținut deîmpărțitul
este egal cu avem aici împărțitorul
înmulțit cu câtul adunat cu Ce
este unu unu este restul bun si
am obținut Aici este se numește
teorema împărțirii cu rest voi
scrie prescurtat a HD la teoremă
împărțirii cu rest bun Haideți
să ștergem ai se vadă am scris
teorema împărțirii această teoremă
o Vom folosi în diferite exerciții
însă mai întâi Haideți să vedem
Care este relația dintre rest și
împărțitor vede să ne uităm puțin
la exemplul nostru după ce am distribuit
câte o minge în fiecare cutie ne
au mai rămas patru mingi the Cube
4 este un număr mai mare decât
trei trei fiind împărțitorul reprezentat
de aceste cutii am putut să continuăm
această distribuire bun dar până
când am continuat distribuirea
până când restul a devenit mai
mic decât numărul de cutii adică
până când restul a devenit strict
mai mic decât împărțitorul să știți
că întotdeauna restul este strict
mai mic decât împărțitorul și cum
restul e un număr natural vom trece
fiere este un număr mai mare sau
egal cu zero vom urmări această
inegalitate și pe parcursul exercițiilor
noastre și acum Haideți să facem
câteva împărțiri 246 împărțit la
13 Haide să facem acest calcul
13 Nu Se cuprinde în doi însă Se
cuprinde în 24 se cuprinde o singură
dată pentru că dacă am Treci aici
doi doi ori 13 de 26 deja a trece
de 24 ce facem apoi facem scăderea
avem aici 1 și aici 1 facem o scurtă
observație aici Care e destul de
importantă a zice eu și anume aceea
că întotdeauna la acest pas Când
se fac aceste tipuri de scăderi
pe parcursul unei împărțiri Nu
contează că suntem la începutul
împărțirii la mijloc sau la final
întotdeauna numărul care se obține
în urma a scăderii este mai mic
decât împărțitorul iar de 11 strig
mai mic decât 13 dacă ce obținem
Aici este un număr mai mare înseamnă
că pe undeva sa strecurat o am
încheiat această observație care
sters va fi de folos și acum am
făcut scăderea coborâm următoarea
cifra deîmpărțitului 13 De câte
ori se cuprinde în 116 Păi Haideți
să vedem dacă facem 13 înmulțit
cu 8 de exemplu avem opt ore 324
84 și 2 în minte 8 ori 8 cu 2 din
minte 10 104 dacă am face 13 ori
nouă să vedem dacă ne apropiem
mai mult de 116 bun de fapt rebuie
să îl adunăm pe 104 cu 13 și o
să ne dea 117 deja trece de acest
număr asta înseamnă că vom trece
aici numărul opt opt ori 13 ne
dă 104 facem scăderea 6.104 2 1
1 0 160 a rămâne nimic ce am obținut
Păi am obținut că 246 împărțit
la 13 ne dă 18 rest 12 Cum verificăm
dacă împărțirea pe care am efectuat
o este făcută corect Păi proba
împărțirii e dată de fapt chiar
de teorema împărțirii cu rest care
ce ne spune ne spune că deîmpărțitul
egal cu împărțitorul ori câtul
plus restul cu alte cuvinte Haideți
să verificăm dacă deîmpărțitul
adică 246 este o are egal cu 13
ori 18 Adică ori câtul adunat cu
restul adică cu 12 Păi 13 ori 18
ne dă 234 Puteți să faceți acest
calcul plus 12 mai vedem că dacă
adunăm doi cu 4 6 1 cu 3 4 și acest
2 deci am obținut o relație adevărată
Am efectuat și Proba împărțirii
ce mai Observă cum este restul
față de împărțitor restul este
strict mai mic decât împărțitorul
12 este Street mai mic decât 13
Haide să notăm aici restul Street
mai mic decât împărțitorul încă
un exemplu să facem această împărțire
48.000 325 împărțit la 300 Păi
de fapt 300 nu se cuprinde nici
în patru mici în 48 dar în 483
se cuprinde o dată unul ori 300
ne dă 300 facem scăderea avem aici
trei aici avem opt și aici nu ne
rămâne unul pardon Deci Haideți
să ștergem era să facem o greșeală
Deci ne rămâne aici unu Ce observăm
poiată ca acest număr cu 183 de
după ce am făcut scăderea este
Cum este strict mai mic decât împărțitorul
un am făcut scăderea coborâm acum
pe 2 300 de câte ori se cuprinde
în 100 în 1832 Păi se cuprinde
de 6 ori 7 deja ar fi prea mare
și avem aici 1800 facem scăderea
Avem doi trei minute zero 360 nimic
și nimic din nou după această scădere
cât am obținut 32 Care este strict
mai mic decât 300 Da coborâm acum
și pe cinci 300 Se cuprinde în
325 o singură dată deci trecem
1 ori 300 300 și ne rămâne aici
cinci aici 260 nimic Deci avem
48.000 325 împărțit la 300 câteodată
161 rest 25 case efectuam proba
împărțirii ce trebuie să facem
trebuie să vedem dacă deîmpărțitul
egal cu împărțitorul înmulțit cu
câtul adunat cu restul Și aici
e ușor de făcut acest produs de
fapt înmulțim pe 3 cu 161 și la
final adăugăm 20 ori 3 ori 1 ne
dă 3 trei ori 6 ne dă 18 Deci 8
și 1 în minte 3 ori 1 3 1 din minte
4 adăugăm cele două zerouri plus
25 pe Clark obținem 48300 25 Deci
am făcut un calcul corect avem
o relație adevărată din nou Ce
relație este între rest și împărțitor
restul este strict mai mic decât
împărțitorul din nou voi scrie
și în paranteză acest lucru mai
facem încă un exemplu și avem o
împărțire simplă 21 împărțit la
7 Păi 7 intră în 21 de trei ori
trei ori 7 ne dă 21 de ce am făcut
această împărțire pentru că vorbim
aici de o împărțire exactă este
Cică împărțirile exacte pot fi
considerate și le împărțiri cu
rest în să vorbim aici de rest
0 Deci notăm că 21 împărțit la
7 se poate scrie ca fiind egal
cu 3 în rest 0 și în această situație
putem să facem verificarea adică
proba împărțirii verificăm dacă
deîmpărțitul egal cu împărțitorul
ori câtul plus restul Haideți să
vedem 21 este întradevăr egal cu
7 ori 3 plus zero avem aici o relație
adevărată cu alte cuvinte Haide
să reținem această relație care
ne spune că deîmpărțitul este egal
cu împărțitorul și tonul ori câtul
plus restul și să reținem și faptul
că restul este un număr natural
mai mare sau egal cu 0 și este
întotdeauna strig mai mic decât
împărțitorul

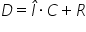 ,
,