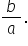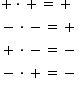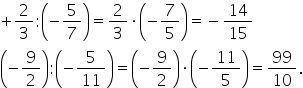Împărțirea numerelor raționale
Tag-uri
Partajeaza in Google Classroom
Transcript
Fie a și b două numere întregi
diferite de 0 atunci Inversul numărului
rațional a supra b este numărul
b supra a de exemplu Inversul numărului
rațional minus 5 supra 6 va fi
minus 6 supra 5 semnul din fața
numărului se păstrează și se inversează
fracția având în vedere că împărțirea
a două fracții se reduce la a înmulțit
prima fracție cu invers a celei
de a doua regula semnelor rămâne
valabilă și la împărțire prima
împărțire plus 2 supra 5 împărțit
la minus 4 supra 7 pentru a împărți
două fracții înmulțim prima fracție
cu invers a celei de a doua Semnul
plus nu se mai scrie va fi egal
Așadar cu 2 supra 5 ori minus 7
supra 4 pe diagonală putem să simplificăm
cu 2 4 împărțit la 2 este 2 plus
ori minus este minus 7 supra 10
al doilea exercițiu minus 2 supra
7 împărțit la minus 3 supra 14
egal cu minus 2 supra 7 ori minus
14 supra 3 Putem să simplificăm
pe diagonală cu 7 deoarece 14 este
un multiplu al lui 14 împărțit
la 7 este 270 la 7:00 este 1 obținem
minus 2 supra 1 ori minus 2 supra
3 minus ori minus este Plus 2 ori
2 este 4 anul 3 este 3 adică egal
mai departe cu 4 supra 3 al treilea
exercițiu 8 împărțit la minus 16
supra 3 este egal cu opt ori minus
3 supra 16 putem să simplificăm
cu 816 împărțit la 8 este 2 8 împărțit
la 8 este cu 1 plus ori minus este
minus 3 supra 2 al patrulea exercițiu
minus 1 supra 9 împărțit la 4 supra
27 a egal cu minus 1 supra 9 ori
27 supra 4 27 se împarte la 9 rezultatul
împărțirii este 3 iar 9 împărțit
la 9 este 1 minus ori plus este
minus 1 ori 3 3 supra 1 ori 4 4
Împărțirea numerelor raționaleAscunde teorie X
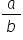întelegem fracția 
Navigare în lectii
Cumpara abonament
