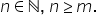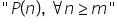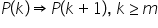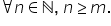Inducția matematică - aplicații
Tag-uri
Partajeaza in Google Classroom

Transcript
în acest film ne propunem să demonstrăm
formula de calcul pentru suma pătratelor
primelor n numere naturale respectiv
formula de calcul pentru suma cuburilor
primelor n numere naturale folosind
metoda inducției matematice și
începem cu primul exercițiu să
se demonstreze că 1 la pătrat plus
2 la pătrat plus 3 la pătrat plus
puncte puncte plus n la pătrat
este egal cu n pe lângă n plus
1 pe lângă 2 ani plus 1 supra 6
oricare ar fi n număr natural diferit
de 0 începem cu prima etapă etapa
de verificare verificăm dacă propoziția
pe DN este adevărată pentru prima
valoare pe care o poate lua n prin
urmare Dacă n este egal cu 1 avem
propoziția pe de 1 care se obține
înlocuind pe n cu 1 atât în membrul
stâng cât și în membrul Drept și
avem unul la pătrat egal cu 1 pe
lângă 1 plus 1 pe lângă 2 ori 1
plus 1 totul supra 6 1 va fi egal
cu unu plus unu este doi doi plus
unu este 3 totul supra 6 6 supra
6 este 1 Așadar are loc egalitatea
1 egal cu 1 Deci propoziția pe
D1 este adevărată putem să verificăm
și propozițiile pe de doi și pe
trei dar nu este obligatoriu așa
a fost să continuăm cu a doua etapă
demonstrația demonstrăm că are
loc implicația pdk implică pdk
plus 1 oricare ar fi ca apa un
număr mai mare sau egal cu 1 pentru
aceasta o Să presupunem că propoziția
pdk este adevărată și pe baza acesteia
demonstrăm că propoziția pdk plus
unu este adevărată o să scrie mai
întâi propoziția pe Dica Înlocuim
pe n cu k atât în membrul stâng
și membrul drept și avem unul la
pătrat plus 2 la pătrat plus 3
la pătrat plus puncte puncte plus
ca la pătrat egal k pe lângă k
plus 1 pe lângă 2 k plus 1 totul
supra 6 iar aceasta este propoziție
adevărată Acum scrie în propoziția
predica plus 1 ultimul termen în
această propoziție va fi ca plus
1 la pătrat dar o să scriem și
termenul situat înaintea acestuia
iar acesta va fi k la pătrat avem
unul la a doua plus 2 la a doua
plus puncte puncte plus k la pătrat
plus ultimul termen capusanu la
pătrat egal în această formulă
Înlocuim pe n cu k plus 1 și obținem
k plus 1 pe lângă k plus unu plus
unu este k plus 2 aici o să avem
2 pe lângă k plus 1 plus 1 totul
supra 6 egal o să mai facem calculele
în paranteză dreaptă și obținem
k plus 1 pe lângă k plus 2 pe lângă
2k plus 2 plus 1 este 2 k plus
3 totul supra 6 aceasta este propoziția
pe Dica plus unu nu știm dacă este
adevărată însă vrem să demonstrăm
acest lucru observăm că în cadrul
expresiei pe Dica plus 1 regăsim
această sumă Care este de fapt
propoziția pe dk din moment ce
propoziție a pedica este adevărată
înseamnă că această sumă poate
fi înlocuită cu această formulă
și atunci să vedem ce obținem că
apa pe lângă k plus 1 pe lângă
2 k plus 1 totul supra 6 urmează
apoi acest termen plus k plus 1
la pătrat egal mâna factor comun
paranteza ca plus 1 avem k plus
1 k a pe lângă 2 k plus 1 supra
6 las k plus 1 egal aici o să aducem
la numitor comun amplificăm cu
6 și avem ca plus 1 pe lângă k
ori 2 k plus 1 plus 6k plus 6 totul
supra 6 egal k plus 1 ori desfacem
aici paranteza 2 k la pătrat plus
K A și plus 6 k este 7 k plus 6
totul supra 6 egal acum luăm de
7k o să scriem 4K plus 3 k pentru
a putea da factor comun filmare
o să avem k plus 1 pe lângă 2 k
la pătrat plus 4K plus 3 k plus
6 totul supra 6 egal k plus 1 pe
lângă din primii doi de factori
comun pe 2 k și avem 2 k pe lângă
k plus 2 plus din ultimii doi termeni
de factor comun pe 3 3 pe lângă
k plus 2 și aici avem o paranteză
dreaptă totul supra 6 egal observăm
că în paranteză dreaptă mai putem
da factor comun pe k plus doi avem
k plus 1 pe lângă k plus 2 pe lângă
2 k plus 3 totul supra 6 dacă ne
uităm la Formula aceasta la care
am ajuns și la Formula pe care
o regăsim în cadrul expresiei pe
Dica plus 1 observăm că avem o
egalitate prin urmare propoziția
pe de că a plus unu este adevărată
înseamnă că are loc implicația
pe de ca implică pe de cablu nu
așa Dai propoziția pe DN este adevărată
oricare ar fi n număr natural diferit
de zero și în continuare mai facem
un exercițiu să se demonstreze
folosind metoda inducției matematice
că are loc următoarea egalitate
1 la a treia plus 2 la a treia
plus 3 la a treia plus și așa mai
departe plus n la a treia egal
cu n pe lângă n plus 1 supra 2
totul la pătrat unde n este număr
natural diferit de zero începem
cu etapa de verificare verificăm
dacă este adevărată propoziția
pe D1 pe de unul se obține înlocuind
pe nu1 atât în membrul stâng cât
și membru în Drept avem unul la
a treia egal cu 1 pe lângă 1 plus
1 supra 2 totul la pătrat 1 la
a treia este unul aici se simplifică
doi cu doi și rămâne unul la a
doua adică unul prin urmare avem
o egalitate Deci propoziția pe
D1 este o propoziție adevărată
urmează etapa a doua demonstrația
arătăm care loc implicația pe Dica
implică pe de capul sună oricare
ar fi ca apa un număr mai mare
sau egal cu 1 presupunem că propoziția
pdk este adevărată și demonstrăm
că pe Bica plus unu este adevărată
scrie în propoziția pe Dica Înlocuim
pe n cu k și obținem 1 la a treia
plus 2 la a treia plus 3 la a treia
plus puncte puncte plus k la a
treia egal cu k pe lângă k plus
1 supra 2 totul la a doua Aceasta
este o propoziție adevărată acum
Avem propoziția petca plus 1 Înlocuim
pe n cu k plus 1 ultimul termen
al sumei va fi capul sub nu la
a treia penultimul termen va fi
k la a treia și o să îl scriu și
pe acela tocmai pentru a evidenția
faptul că în expresia lui pdk plus
1 regăsim propoziția PDF Așadar
o să avem unul la treia plus 2
la a treia plus 3 la a treia plus
puncte puncte plus ca la a treia
plus ca plus 1 la a treia egal
ca plus 1 pe lângă k plus unu plus
unu Deci k plus 2 supra 2 totul
la pătrat iar această expresie
se poate scrie mai departe ca plus
1 la pătrat pe lângă ca plus 2
la pătrat totul supra 4 observăm
că în cadrul propoziției PD plus
1 ne găsim această sumă aceasta
este propoziția pdk din moment
ce PD ca este adevărată înseamnă
că putem înlocui această sumă cu
formula aceasta de mai sus și atunci
o să avem k pe lângă k plus 1 supra
2 totul la pătrat plus k plus 1
la a treia egal aici și trebuie
să pun paranteze pătrate dar mie
nu prea îmi plac parantezele pătrate
așa că o să pun rotund dar voi
să Scrieți corect și frumos ridicăm
la pătrat și avem capela pătrat
pe lângă a plus 1 la pătrat totul
supra 4 plus ca plus 1 la a treia
egal putem să dăm factor comun
ca plus 1 la a doua și obținem
ca plus 1 la pătrat pe lângă capela
pătrat supra 4 plus k plus 1 vinil
amplificăm cu patru avem ca plus
1 la pătrat ori ca la a doua plus
4K plus 4 totul supra 4 egal capul
sunt la pătrat ori aici avem expresia
că apa plus 2 totul la pătrat supra
4 încadrăm formula la care am ajuns
și iată care îi găsim aceeași formulă
de mai sus Așadar prepoziția pe
D că a plus unu este adevărată
prin urmare implicația are loc
Așadar propoziția pe DN este adevărată
oricare ar fi n număr natural diferit
de 0