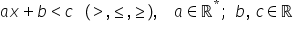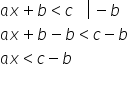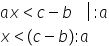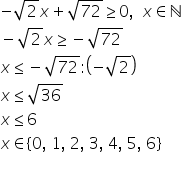Inecuații cu coeficienți reali
Tag-uri
Partajeaza in Google Classroom

Transcript
o inecuatie este o propoziție matematică
cu o variabilă în care apare unul
din semnele mai mic mai mare mai
mic sau egal mai mare sau egal
un număr întreg Este o soluție
a inecuației dacă înlocuind necunoscuta
cu acel număr se obține o propozitie
adevărată pentru a rezolva inecuațiile
vom face operații succesive în
ambii membri ai inegalității astfel
încât să separăm necunoscuta x
de cere alți termeni și să obținem
valori posibile ale necunoscutei
x de reținut că atunci când înmulțim
sau împărțim ambii membri ai unei
inecuații cu un număr negativ semnul
inegalității se schimbă faci un
exercițiu cerința exercițiului
este următoarea Rezolvați în mulțimea
numerelor naturale următoarele
inecuații la punctul a mic avem
minus radical din 2x plus radical
din 72 este mai mare sau egal decât
0 în prima etapă Încercăm să facem
o operație astfel decât în membrul
stâng al inecuației se rămână doar
termenul în care conține necunoscuta
x pentru a elimina pe radical din
72 din membrul stâng va trebui
să scădem acest radical din ambii
membri ai Egalității pentru că
radical din 72 minus radical din
72 va fi 0 iar în membrul stâng
va rămâne minus radical din 2x
acesta este mai mare sau egal decât
minus radical din 72 între minus
radical din 2 și x avem operația
de înmulțire pentru a elimina coeficientul
din față a lui x trebuie să facem
operația inversă înmulțirii adică
împărțirea Așadar împărțim ambii
membri a inecuației la minus radical
din 2 atenție minus radical din
2 este număr negativ Deci se va
schimba semnul inecuației obținem
x mai mic sau egal decât minus
radical din 72 împărțit la minus
radical din 2 x va fi mai mic sau
egal decât radical din 36 x va
fi mai mic sau egal decât 6 pentru
că trebuie să rezolvăm această
in ecuație în mulțimea numerelor
naturale valorile posibile ale
lui x vor fi 0 1 2 3 4 5 și 6 x
trebuie să fie număr natural a
doua in ecuație minus x radical
din 5 plus radical din 45 este
mai mare decât 0 ca să eliminăm
pe radical din 45 o să scădem acest
număr din ambii membri ai inecuației
minus x radical din 5 va fi mai
mare decât 0 minus radical din
45 adică minus radical din 45 putem
acum să înmulțim această in ecuație
cu minus unu pentru a elimina semnul
minus din ambii membri ai inecuației
obținem x radical din 5 mai mic
decât radical din 45 între x și
radical avem înmulțire așa dar
trebuie să împărțim la radical
din cinci obținem x mai mic decât
radical din 45 împărțit la radical
din 5 x va fi mai mic decât radical
din 9 aici Am aplicat o formulă
de calcul cu radicali radical din
a împărțit la radical din b este
radical din a împărțit la b si
mai avem și următoarea formulă
radical din a ori radical din b
este radical din a ori b Am vrut
doar să reamintesc acestei formule
deja de cal din 45 împărțit la
radical din cinci va fi radical
din 9 x este mai mic decât 3 numerele
naturale mai mici strict decât
3 sunt 0 1 și 2 x aparține mulțimii
0 1 și 2 următoarea ecuație minus
4x plus 11 mai mare decât 0 o să
îl scădem pe 11 din ambii membri
și obținem minus 4 x mai mare decât
minus 11 putem să împărțim la minus
4 și avem x mai mic decât minus
11 împărțit la minus 4 minus împărțit
la minus va fi plus și acum se
face 11 împărțit la 4 411 se cuprinde
de două ori 2 ori 4 este 8 efectuez
căderea adăugăm în 04 în 30 intră
de șapte ori șapte ori 428 efectuăm
scăderea adăugăm un zero patru
în 20 intră de cinci ori cinci
ori 420 am obținut că x este mai
mic decât 2 x trebuie să fie număr
natural pentru că așa era cerința
exercițiului iar numerele naturale
mai mici strict decât 2 vor fi 0
1 și 2 și punctul de ultima ție
x supra 2 minus x supra 3 mai mic
decât doi în membrul stâng Avem
două fracții cu numitori diferiți
asa putem efectua această scădere
aduce în fracțiile la același numitor
numitorul comun va fi 6 amplificăm
prima fracție cu trei și a doua
fracție cu 2 obținem 3x supra 6
minus 2x supra 6 mai mic decât
doi putem scrie o singură linie
de fracție 3x minus 2x totul supra
6 mai mic decât doi 3x minus doi
x este x supra 6 mai mic decât
doi Asta eliminăm numitorul o să
înmulțim această ecuație cu 6 fac
alăturat un mic calcul șase ori
x supra 6 se simplifică șase cu
șase și rămâne x Deci nu mai stăm
o să avem x mai mic decât doi ori
6 x să fie mai mic decât 12 x aparține
mulțimii 0 1 2 3 și așa mai departe
ultimul număr va fi 11 pentru că
x trebuie să fie strict mai mic
decât 12