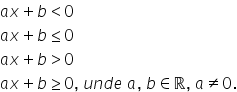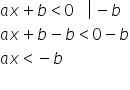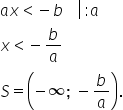Inecuații de gradul I

în această lecție vom continua

recapitularea ecuațiilor shin ecuațiilor

de gradul întâi și mai clar vom

face referire la inecuațiile de

gradul întâi Forma generală inecuații

de gradul unu este dată de ax plus

pe mai mare ca 0 ax plus pe mai

mare sau egal decât 0 ax plus b

mai mic decât 0 respectiva ax plus

b e mai mic sau egal decât cel

Unde în mod Evident a este diferit

de 0 respectiv a și b sunt numere

reale în practică variabila x este

în realitate delimitată la stânga

sau la dreapta de valoarea minute

pe supra amintesc că a minus b

supra era soluția ecuației de gradul

întâi adică atunci când în ecuație

apare semnul mai mare sau semnul

mai mare sau egal se face referire

la valorile pe care variabilă x

le poate pe dreapta valori în minus

pe supra a atunci când inecuația

apare semnul mai mic sau mai mic

sau egal se face referire la valorile

pe care le poate avea în stânga

valorii minus b supra a astfel

că dacă propun spre rezolvare inecuația

x plus b mai mare decât 0 în realitate

înțeleg De fapt că IX va fi mai

mare decât minus p respectiv pixul

mai mare decât minus 3 supra a

astfel în această situație în situația

rezolvării inecuații se așteaptă

ca rezultat un interval în cazul

de față un interval deschis și

pe tete minus b supra a plus infinit

în cazul în care în propoziții

rezolv ax plus pe mai mare sau

egal decât 0 pe exact același principiu

de rezolvare voi obține intervalul

închis de această dată la minus

b supra a plus infinit închis puneam

din cauza faptului că în inecuația

apare semnul mai mare sau egal

din cauza egalului pentru înțelegere

cât mai exactă Reprezentăm pe axa

reală valoarea minus b supra a

și mă interesează în mod cert valorile

pentru care x sunt mai mari decât

acest minus pe supra mai clar valorile

din dreapta 2 minus pe supra ei

așa cum este evidențiat cu albastru

pe axa real un aspect Important

este că intervalul închis exprimat

în a doua situația inecuații da

Va trage de la sine că intervalul

soluții ale inecuației va conține

și valoarea minus b supra a în

cazul în care ne propunem să rezolvăm

inecuația x plus b mai mic decât

sero la fel ai mai mic decât minute

adică x mai mic decât minus pe

supra rezultatul sau soluție inecuații

este intervalul x aparține intervalului

așa cum vedeți minus infinit minus

b supra a interval deschis după

cum Observați vorbim de valorile

din stânga valori în minus pe supra

fără ca ea să fie cod Newton intervalul

soluției pe același aspect dar

de această dată cu mai mic sau

egal va avea drept rezultat soluție

da intervalul minus infinit minus

b supra de această dată așa cum

spuneam închis la minus b supra

a la fel pe axa reală evidențiată

partea din stânga a valorii minus

pe supra adică pentru x mai mic

decât minus b supra Da evidențiată

așa cum neam obișnuit cu albastru

da Și mai clar situația în care

este conținută și valoarea minispir

supra adică în intervalul închis

situația în care inecuația noastră

conține semnul mai mic sau egal

da pe exemplul dat în lecția precedentă

cel cu tricourile puteți interpreta

că în cazul inecuațiilor prețul

de 45 de RON pentru trei tricouri

este sau nu depăși este depășit

când vorbim de valurile din dreapta

și nu este depășit de semi Mitea

sălacea valoare pentru valorile

din stânga astfel că pe prima situație

Da vorbim de preț depășit mai clar

prețul unui produs Da unui tricou

în cazul nostru va fi mai mare

de 15 RON și a doua situație în

mod Evident situația în care nu

este depășit prețul Deci prețul

va fi mai mic decât 15 RON pentru

un tricou propun în continuare

un exemplu în care vi se cere sau

ni se cere să rezolvăm inecuația

x plus 4 mai mare decât minus 2x

plus 3 pentru rezolvarea inecuațiilor

raționamentul de rezolvare se aseamănă

foarte mult cu cel utilizat la

ecuații singura diferență constă

în tipul de rezultat obținut mai

clar ecuațiile au drept rezultat

o rădăcină Adică o valoare inecuațiile

au drept rezultatul un interval

astfel că inecuația propusă spre

rezolvare și anume x plus 4 mai

mare decât minus 2x plus 3 va trece

de la sine așa cum obișnuit de

la ecuații separarea termenilor

ce conțin necunoscuta x în partea

stângă Da și termenii si nu conțin

variabila x în partea dreaptă Sper

că x sul Da rămâne la locul lui

și își păstrează semnul minus 2x

vine din dreapta în stânga cu sens

schimbat meci a venit plus 2 pe

exact același principiu trei rămase

locului minus patru a venit cu

semn schimbat astfel că obțin 3

x mai mare decât minus 1 ceea ce

înseamnă fără doar și poate că

x este mai mare decât minus 1 pe

3 astfel că soluția inecuației

date va fi intervalul deschis minus

1 pe 3 plus infinit dacă în loc

de mai mare avea mai mare sau egal

În exemplul precedent am fi obținut

intervalul închis minus 1 pe 3

plus infinit cu mod mod Evident

raționamentul de calcul același

urmat ca în exemplul precedent

propun în continuare un alt exemplu

templu probabil sau puțin mai complicat

sensul în care va atrage de la

sine și desfacerea unei paranteze

și separarea termenul așa cum neam

obișnuit și anume 4 pe lângă șase

minute mai mare sau egal decât

3 pe lângă x minus 13 și atunci

se desfac parantezele așa cum vă

spuneam se obține 24 x 4 x mai

mare sau egal decât x minus 39

separăm termeni așa cum obișnuit

minus 4x minus 3 x mai mare sau

egal decât minus 39 24 adică minus

7 x mai mare decât minus 63 de

ce acest exemplu pentru că prezintă

o situație specifică și clară în

cazul inecuațiilor și anume coeficientul

variabilei noastre variabila a

este minus 7 Acesta este un coeficient

negativ citeste motivul pentru

care sîntem obligați să înmulțim

inecuația noastră cu minus unu

pentru a schimba semnul cum spuneam

coeficientului variabilei ma Ce

înseamnă asta înseamnă două aspecte

și anume că se va Nu ții cu minus

unu atât minți 7 cât și mie nu

știai cât și minus 63 dar foarte

foarte important are ca efect înmulțirea

sa schimbarea semnului coeficienților

așa cum cum neam prost dar foarte

foarte important va avea că ai

fix și schimbarea sensului inegalității

ce vreau să spun cu asta în acest

moment în mai avem în inegalitate

inecuația mai mare sau egal schimbarea

sensului presupune transformarea

lui mai mare sau egal în mai mic

sau egal adică așa cum spuneam

nici nu 7 strat forma 7 x minus

63 se transformă 63 mai mare sau

egal se va transforma în mai mic

sau egal deci atunci când intru

in ecuație coeficientul variabilei

pe care le propune să determinăm

dacă ai interval ca soluție va

fi negativ suntem obligați să înmulțim

cu minus 1 minus unu Ăsta are ca

efect odată schimbarea semnului

coeficientului sau coeficienților

din inecuații și foarte important

schimbarea sensului inegalități

astfel că x va fi mai mic decât

63 pe 7 adică x va fi mai mic sau

egal decât 9 Deci soluția noastră

va fi intervalul minus infinit

9 închis la 9:00 din cauza egalului

un tip de ecuații ce derivă din

ecuații respectiv inecuații de

gradul întâi sunt ecuațiile ce

conțin necunoscuta în modul este

necesar fără discuții să reamintesc

următorul aspect legat de modulul

sau valoarea absolută a unei nunți

modul de a va fi a dacă ai este

pozitiv de exemplu modul de 7 700

pozitiv va avea ca rezultat 7 modul

de 0 avea ca rezultat 0 și foarte

important modul de o valoare negativă

Deci dacă a este negativ rezultatul

va fi în minus acea valoare negativă

Asta înseamnă dacă am modul de

minus 7 acesta va fi minus minus

șapte Deci mai clar modulul Transformă

sau valoarea absolută Da transformă

în plus ce valoare negativă sau

pozitivă un exemplu ce conține

necunoscuta modul voi avea modul

de x plus 2 va fi x plus y dacă

x plus 2 este mai mare decât 0

0 dacă x este x plus 1 este egal

cu 0 respectiv minus x plus doi

dacă x plus 2 este mai mic decât

astăzi că modul de x plus doi va

fi de fapt x plus 2 dacă x este

mai mare decât minus 2 ceea ce

înseamnă interval deschis minus

2 plus zero dacă este egal cu minus

2 respectiv minus x minus 2 plus

minus în fața parantezei schimbă

semnele tuturor termenilor din

paranteză așa cum spuneam Venus

x minus 2 Pentru x mai mic decât

minus doi Deci x aparține intervalului

minus Infinit 2 dec stânga da pe

care vo propun în continuare sună

Cam așa să se rezolve ecuația modul

de șase minute se calcula spray

foarte important este că trebuie

să priviți rezolvarea acestei ecuații

pe etape în prima etapă se face

fără doar și poate explicitarea

modulului Modul în cazul nostru

6 minus x Da Acesta va fi 6 minus

x dacă 6 minus x este mai mare

decât zero va fi 0 Dacă șase minute

este egal cu 0 respectiv minus

6 plus de descompus minus în fața

parantezei Da care va va fi din

șase că zic așa cum spuneam pentru

6 minus x mai mic decât cel foarte

important este că modulul nostru

se va rezuma sau va avea drept

rezultat 6 minus x pentru x mai

mic decât 6 Ce observați că Dinu

Da are coeficient negativă au plecat

așa cum vă comenta mai sus să înmulțesc

cu minus unu ceea ce a atras de

la sine o dată schimbarea semnelor

coeficientul și foarte important

schimbarea sensului inegalități

Deci mai mare sa transformat în

mai mic continuăm 0 Dacă x egal

cu 6 respectiv x minus 6 dacă x

este mai mare decât șase în etapa

următoare se rezolvă ecuația inițial

ecuația dacă pe cele trei situații

apărute în urma explicită rii modulului

la etapa 1 astfel că în situația

în care nu am propus să discut

pentru x aparține lui e 6 plus

infinit Da soluția sau modul nostru

de venea x minus 6 în situația

în care discutam pentru x egal

cu 6 modul nostru de Finanțe respectiv

situația treia stație în care discutăm

pe x aparține intervalului minus

infinit 6 modul nostru de venea

6 minus x pe Motivează astfel următoarea

etapă și anume sub formă de tabel

redactarea rezolvării este la îndemâna

oricui și mi se pare cât se poate

de reprezentativă așa cu tabel

și anume pe primul rând al tabelului

septic valorile lui x valorile

intervalele în care acesta se se

desfășoară și pe a doua linie Da

sau pe al doilea rând ecuația noastră

astfel că au apărut valorile minus

infinit 6 respectiv pentru că vorbim

de interval 6 plus infinit valoarea

6 respectiv intervalul minus infinit

7 astfel că în situația în care

discutăm de intervalul minus infinit

Șase Da suntem aici Da modul nostru

așa cum spuneam niste șase minute

și atunci șase minute va fi egal

cu 2x minus 3 dacă vorbim pentru

x egal cu 6 sau ne referim la stric

valoare x egal cu 6 modulul nostru

așa cum spuneam este 0 și atunci

vorbim despre 0 egal cu 2x plus

3 un epitet următoarea etapă dacă

discutăm pe intervalul 6 plus infinit

discutăm de x minus 6 egal cu 2x

plus 3 mod de viteză se rezolvă

fiecare din aceste situații și

anume clar 3x egal cu 3 de unde

x egal cu 1 pe situat x aparține

intervalului minus infinit șase

situații x egal cu 6 voi avea 2

x egal cu minus 3 ceea ce înseamnă

că x egal cu minus 3 pe 2 pe situația

treia intervalul 6 plus infinit

x aparține lui 6 plus infinit așa

cum știm x sunt o parte Da în partea

stângă termice conțin x termice

nu conțin x în partea dreaptă rezolvare

clasică x va fi egal cu minus 9

foarte important De înțeles în

acest moment este că 1 soluția

obținută pe intervalul minus infinit

6 este sau aparține intervalului

de discuții Deci 1 aparține intervalului

minus infinit 6 ceea ce atrage

de la sine Ok Aceasta este o soluție

a ecuației ajung în sala situație

și anume x ia dat minus trei pe

doi discutam însă pentru x egal

cu 6 ceea ce ar însemna că șase

ar trebui să fie egal cu minus

3 pe 2 Nu este adevărat Da Atunci

avem o situație falsă înțelegând

din aceasta că x egal cu 6 nu este

soluția a ecuației dat a treia

și ultima situație este aceea în

care am obținut soluția x egal

cu minus 9 discutând însă pe intervalul

6 plus infinit înțeleg că nici

aceasta nu aparține intervalului

de discuție Deci înțeleg iar că

am un fals da o relație falsă Deci

nici minus 9 nu este rădăcina este

soluție a inecuației tot astfel

că ai ecuației date astfel că concluzii

finală soluția ecuației date este

x egal cu 1