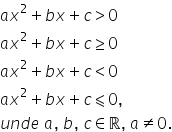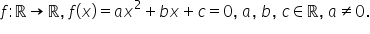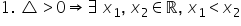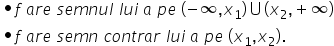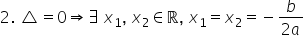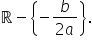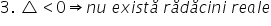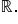Inecuații de gradul II

până această lecție ne vom opri

asupra al ecuațiilor de gradul

al doilea Forma generală a acestor

tipuri de inecuații este ai pătrat

plus bx plus c mai mare decât 0

mai mare sau egal decât 0 mai mic

decât 0 respectiv mai mic sau egal

decât 0 cu epitet apeși Ce coeficienți

reali rezolvarea ecuațiilor de

gradul al doilea este o consecință

imediată a studiului semnului funcției

de gradul al doilea pentru o funcție

de gradul 2 x egal cu x pătrat

plus bx plus c cu a b și c b a

se distingeau următoarele situații

teoretice prima situație atunci

când Delta era pozitiv fdx sul

va avea avea semnul lui a pe intervalul

minus infinit X1 reunit cu x 2

plus infinit respectiv f de x are

semn fluier pe intervalul X1 X2

mai mult decât atât la vremea respectivă

Explică în exteriorul rădăcinilor

vorbim de semnul lui A iar în interiorul

rădăcină vor vinde semnul contrar

lui a 2-a situație teoretică pe

alta era egal cu 0 în cazul acesta

epic avea semnul lui a pentru a

pozitive Teixeira mai mare sau

egal ca 0 pa reamintesc că ținea

apă cu un exprimam și atingea axei

întru un singur punct acela fiind

rădăcina X1 care citea cu X2 dacă

era negative x era mai mic sau

egal decât 0 atunci când te tai

este negativ nu avem rătăcire ale

adică nu atinge asta nu intersectat

deloc axa o x r pentru care e fixul

avea semnul lui astfel că pentru

a pozitiv RDX era strict mai mare

decât 0 Da pe spuneam Nu atingi

axa o x respectiv pentru a negative

trixera negativ în aceste condiții

o in ecuație de gradul al doilea

poate fi rezolvată astfel în prima

etapă să se rezolve ecuația de

gradul 2 corespunzătoare inecuații

tate în a doua etapă se evidențiază

semnul lui a pentru că acesta este

hotărâtor în alege si tu lipsa

porcu inecuația Cine este dată

spre rezolvare se stabilește În

care din situațiile teoretice ne

aflăm în raport cu Delta vă spuneam

putem să fim toate A câta era pozitiv

cântă alta era egal cu situația

b respectiv situația ce când eram

mai mic decât cel în ultima etapă

se stabilește Care este mulțimea

soluțiilor inecuației în raport

de semnul pe care inecuația îl

are respectiv mai mare mai mic

mai mic sau egal respectiv mai

mare sau egal un exemplu și anume

ai spus si mai mare sau egal cu

0 spunea prima etapă sa scoatem

ecuația corespunzătoare inecuației

dată dacă Delta este pozitivă diferite

în situația în care au la rfi pozitiv

Deci are plus Da între rădăcini

am semnul minus în afara rădăcinilor

Semnul plus în cazul în care a

este negativ Deci clar are semnul

minus între rădăcini obsent contrar

adică plus în afara rădăcinilor

am semnal cazul meu inecuația noastră

conține mai mare sau egal Da înseamnă

că mă va interesa Semnul plus și

atunci dacă ai pozitiv mă interesează

aici Deci x va aparține punea în

afara rădăcini drept pentru care

x aparține minus infinit pixul

reunit cu x 2 plus infinit observat

că intervalul este închis datorită

egalului dacă a este negativ la

schimb pe situația negativ cu mă

interesa plus masa aici și atunci

vorbim între rădăcini Deci e sulfa

aparține lui X1 X2 e situația pe

teoretică aș avea Delta egal cu

0 înțeleg din asta că X1 egal cu

x 2 dacă ai pozitiv am Semnul plus

dacă ai negativ de la pozitiv Clar

dacă ai negativ va avea și inecuația

semnul inecuația cazul meu așa

cum spuneam e cu mai mare sau egal

mă interesează În egală măsură

plusuri și atunci mă va trebuie

să această situație pentru a pozitiv

adică x aparține lui r dacă ai

este negativ pixul nu aparține

lui r decât în situația în care

vor vinde X1 ultima situație teoretică

dacă Delta este mai mic decât 0

și evident nu are soluții reale

dacă ai este pozitiv atunci am

semnal prost dacă ai este negativ

atunci am semnul inecuații are

mai mare sau e cald asta înseamnă

că mă interesează cursul Deci mă

va interesa situația 1 discutată

astfel că dacă aude pozitiv vorbim

de xn dacă aul este negativ x nu

aparține lui r practic nu am soluții

reale de ce Pentru că mă interesează

plus și bea negativ Nu am decât

pentru o mai bună înțelegere a

modalității de rezolvare propun

în continuare câteva exemple un

să se rezolve inecuația x pătrat

minus 3x plus 2 mai mare ca 0 în

prima etapă se scoate ecuații aferentă

inecuației tot astfel pătrat minus

3x plus 2 egal cu 0 Delta calculați

valoarea lui este pozitivă rădăcinile

sunt reale și distincte motiv pentru

care din calcul X1 d122 pentru

a egal cu unu Da înțeleg că semnul

lui A deci a coeficientului pătrat

este plus asta înseamnă că pe intervalul

1 2 adică între rădăcini avea semn

contrar lui a umili plus va avea

minute pe intervalul minus infinit

1 reunit cu 2 plus infinit avem

semnul lui a în cazul nostru plus

inecuația dată are semnul mai mare

de de aici în sensul acesta ma

va interesa Semnul plus și atunci

mă uit la ce am gândit pe parcursul

rezolvări plus amplificare în afara

rătăcim concluzia clară este că

x aparține lui minus infinit 1

reunit cu 2 plus IV Observați intervale

deschise întrucât am mai mare strict

Da dacă aș fi avut și că aveam

interval închis la 1 interval închis

la 2 matematică redactarea acestui

rezolvări se face acte pe 3 minus

3x plus 2 mai mare ca 0 ecuația

de gradul 2 Deltă II 1 așa cum

la în calculat respectiv 2 Determinați

1 respectiv 2 pentru ca e calcul

E mai mare ca 0 Deci are Semnul

plus pentru că inecuația mea conține

mai mare înseamnă că mă va intersectat

plus plus și plus înseamnă același

semn pe la același timp vorbim

în afară de condițiile în care

Delta este mai mare ca 0 astfel

soluția problemei mele este x aparține

intervalului minus infinit 1 reunit

cu 2 plus una doilea exemplu pe

care vi propun atenției este 2

pe 3 plus x mai mic sau egal decât

1 se trece în partea cealaltă cu

sens schimbat Deci parte înțelegând

de aici că voi avea tweets pătrat

plus x minus unu mai mic sau egal

decât 0 în acest caz ecuația de

gradul al doilea ce urmează a fi

rezolvată x pătrat plus x minus

1 egal 0 terta este unul plus opt

patru ori minus 1 ori 2 plus 8

este 9 iar Delta pozitiv rădăcinile

sunt reale și distincte comporte

calculului minus 1 respectiv 1

pe 2 în acest moment când a e 2

dispozitiv că am Semnul plus inecuația

noastră este 2 x pătrat plus x

minus unu mai mic sau egal decât

cel dacă văd mai mic sau egal înțeleg

că mă interesează semn și atunci

plus și minus semne diferite sau

semne contrare înțeleg din faptul

că este mai mare ca 0 Da că semne

contrare în interiorul rădăcinii

concluzia clară este că x aparține

intervalului minus unu unu pe doi

iar din ce spun că din cauza faptului

că am și egal intervalul nostru

este închis Dacă aș fi avut intervalul

soluțiilor ar fi fost Unirea și

ultim exemplu este să se rezolve

inecuația x minus 1 la pătrat mai

mare decât 2x minus 3 confort formulei

de calcul prescurtat obții x pătrat

minus 2x plus 1 mai mare decât

2x minus 3 se trec termenii din

dreapta în stânga cu evidență semn

schimbat pătrat minus 4x minus

2x minus 12 cu sens schimbat plus

4 adică 1 minus 3 trece cu sens

schimbat Deci plus 4 mai mare decât

Z ecuația corespunzătoare va fix

pătrat minus 4x plus 4 egal 0 ecuație

pe care dacă o rezolvăm cu Delta

obțin Delta egal cu 0 sau poți

să observi formula de calcul prescurtat

și anume x minus 2 la pătrat egal

cu 0 fac se trece de la sine că

X1 egal cu egal cu doi În condițiile

acestea a este egal cu 1 este mai

mare ca 0 Deci are plus x pătrat

minus 4x plus 4 mai mare decât

0 Iar mă interesează partea pozitivă

avem aceleași semne avem Delta

egal cu 0 și foarte important semnul

de această dată este strict mai

mare Da ceea ce înseamnă că valoarea

2 care este soluție a ecuației

pătrat minus 4x spațiu nu face

decât să ducă la egalitate ori

pe mine mă interesează egal inecuația

mea nu conține mai mare sau egal

în aceste condiții x aparține lui

r mai puțin valoarea 2 o altă modalitate

de rezolvare a ecuațiilor de gradul

al doilea este următoarea și ai

pătrat plus bx plus c mai mare

ca te rog mai mare sau egal ca

0 mai mic ca 0 sau mai mic sau

egal ca 0 în prima etapă se notează

cu e f d x termenul stâng ale inecuației

în cazul meu e f de x egal cu x

pătrat plus bx plus se realizează

tabelul de variație tabelul de

semn dacă vă aduceți aminte al

funcției Eti și în ultima etapă

se alege mulțimea soluțiilor inecuației

Da a pe ăsta pozitiv tabelul de

variație este atunci când am Delta

pozitiv spuneam da ca X1 X2 real

în aceste condiții X1 X2 unde funcția

mea va avea valoarea 0 în exterior

am semnului a în interior contra

lui A atunci când Delta este egal

cu 0 dar nu te va ia ție este următorul

reținem iar că X1 egal cu x 2 RON

da este singura valoare în care

funcția f x este 0 În rest am semnul

lui a pentru Delta negativ tabelul

de variație este dat următorul

tabel înțelegând de aici că nu

am soluții reale da se pot trage

de la sine că x va avea semnul

lui a exemplu nu Să se rezolve

inecuația x pătrat minus 3x plus

2 mai mare ca 0 Observați este

exemplul pe care îl am dat anterior

de această dată îl voi rezolva

cutii sunt cea de a doua modalitate

de rezolvare pe care vom supershow

atenții și așa cum spuneam în prima

etapă Nu te scuip din x partea

stângă sau termenul stâng Alinei

ecuații în cazul meu x pătrat minus

3x plus 2 așa cum aveam comport

calcului Delta ne dădeau 1 x 1

era egal cu 1 x 2 egal cu 2 tabelul

de variații în aceste condiții

de tine în aceste rădăcini valoarea

funcției este 0 în afara rădăcinilor

vorbim de semnul lui a a este 1

Deci pozitiv în sensul ăsta are

plus în interiorul retur semn contrar

lui a aici Poftim desen contrar

în aceste condiții Pe mine mă interesează

partea pozitivă Deci plus Da Și

atunci plus am de la minus infinit

la 1 reunit cu 2 plus semnul este

strict intervalul este deschis

al doilea exemplu pe care îl am

făcut cu prima metodă va fi și

aici tratat astăzi se rezolvă inecuația

2 x pătrat plus x mai mic sau egal

cu 1 se trece unul partea stângă

astfel că obțin 2 pătrat plus x

minus unu mai mic sau egal cu 0

Notes funcția f de x egal cu 2x

pătrat plus x minus unu Delta calculat

era nouă rădăcini determinate erau

minus unu respectiv 1 pe 2 în acest

caz tabelul de variație în minus

1 și 1 pe 2 epic ia valoarea 0

Audi este 2 de 500 pozitivi Adi

care plus semn contrar lui între

rădăcini semnul lui a în afara

rădăcini în acest caz însă vorbim

de mai mic sau adică mă interesează

partea cu mine partea cu mine în

interior soluția inecuației este

x aparține intervalului minus unu

unu pe doi iar fii și spun închis

întrucât inegalitatea mea sau inecuația

mea conține semnul mai mic sau

egal al treilea și ultimul exemplu

să se rezolve inecuația x minus

1 la pătrat mai mare decât 2x minus

3 este x x x pătrat minus 4x plus

4 Delta obținute la zero rădăcinile

erau Ica levitant fiecare cu doi

tabelul de variație singura rădăcina

în această rădăcină vorbim de f

de x egal cu 0 în rest avem semnul

lui a aur este 1 este pozitiv De

ce are plus semnul ia semnul Ia

mă interesează în acest moment

mai mare strict Deci mai testează

și egal cu 0 astea care trage de

la sine că soluția va fi an mai

puțin acest 2 în care e pixul meu

ar face