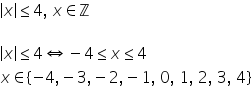Inecuații în Z

o inegalitate de forma x mai mare

decât doi unde x este un număr

întreg se numește inecuația Orice

număr care subt tema aria bilei

x Transformă inegalitatea între

o propoziție adevărată se numește

soluție a inecuației de exemplu

numărul trei este o soluție a inecuației

deoarece 3 este mai mare decât

2 să vedem ce se întâmplă cu această

inegalitate Dacă adunăm în fiecare

membru numărul pozitiv 4 obținem

3 plus 4 mai mare decât doi plus

patru adică șapte mai mare decât

șase observăm că atunci când adunăm

un număr pozitiv la ambii membri

ai inegalității semnul inegalității

se păstrează pornind de la aceeași

inegalitate 3 mai mare decât 2

să scădem numărul 4 din fiecare

membru și obținem 3 minus 4 mai

mare decât 2 minus 4 deoarece minus

1 este mai mare decât minus 2 Așadar

observăm că și Dacă scădem numărul

4 semnul inegalității se păstrează

să vedem ce se întâmplă cu această

inegalitate dacă o înmulțim cu

numărul 4 membru cu membru 3 ori

4 este mai mare decât doi ori patru

adică 12 este mai mare decât 8

observăm că semnul inegalității

se păstrează atunci când o înmulțim

cu un număr pozitiv să vedem ce

se întâmplă dacă înmulțim această

inegalitate cu numărul negativ

minus 4 trei ori minus patru deocamdată

nu scriu semnul pentru că vreau

să fac calculele și doar minus

patru trei ori minus 4 este minus

12 2 ori minus 4 este minus 8 minus

12 este mai mic decât minus opt

observăm că atunci când înmulțim

o inegalitate cu un număr negativ

semnul inegalității se schimbă

această regulă este valabilă și

atunci când împărțim o inegalitate

cu un număr negativ în continuare

să rezolvăm câteva inecuații prima

inecuația x plus 3 mai mic decât

0 unde x este un număr întreg A

rezolva o ecuație înseamnă ai găsit

mulțimea soluțiilor ca și la ecuații

rezolvarea inecuațiilor se reduce

la Găsirea unui șir de transformări

echivalente astfel încât să se

ajungă la o inegalitate destul

de simplă pentru a se putea citi

soluțiile nu proceda ca și la ecuații

vom elimina numărul 3 din membrul

stâng scădem Așadar numărul 3 din

fiecare membru al inegalității

Dacă scădem numărul 3 semnul inecuației

se păstrează și obținem x plus

3 minus 3 mai mic decât 0 minus

3 x va fi mai mic decât minus 3

soluția este formată din numerele

întregi minus 6 minus 5 minus 4

unde prin puncte puncte se înțelege

că acest șir se continuă cu numerele

întregi minus șapte minus 8 minus

9 și așa mai departe Deci avem

o infinitate de soluții și atunci

în general la inecuații Soluția

se va scrie sub următoarea formă

este egal mulțimea formată din

acele numere întregi x cu proprietatea

că x este mai mic decât minus 3

a doua din ecuație 5 x minus 2

mai mic sau egal decât minus șapte

nu mai aduna numărul pozitiv 2

la fiecare membru al inecuației

și obținem 5 x minus 2 plus 2 este

0 de nu o să îl mai scriu mai mic

sau egal decât minus 7 plus 2 5

x mai mic sau egal decât minus

5 asta eliminăm coeficientului

x împărțit la 5 și obținem x mai

mic sau egal decât minus 5 împărțit

la 5 x mai mic sau egal decât minus

1 soluția este formată din acele

numere întregi x cu proprietatea

că x este mai mic sau egal decât

minus 1 continuăm cu 3-a inecuația

minus 2 pe lângă 1 minus 3x mai

mic decât minus opt ca să desfacem

această paranteză folosind distributivitatea

înmulțirii față de scădere așa

dar va trebui să înmulțim numărul

minus 2 cu fiecare număr din paranteză

și obținem minus 2 ori 1 minus

minus 2 ori 3 x mai mic decât minus

opt minus 2 minus aici face mai

întâi înmulțirea în minus 2 ori

3 care este minus 6 x mai mic decât

minus opt minus minus se transformă

în plus și obținem minus 2 plus

6 x mai mic decât minus opt să

eliminăm acest număr minus 2 din

membrul stâng astfel încât să rămână

doar termenul Ce conține necunoscuta

x pentru aceasta va trebui să adunăm

numărul 2 la fiecare membru al

inecuației minus 2 plus 2 la fie

0 și obținem în membrul stâng 6

x mai mic decât minus opt plus

doi 6x va fi mai mic decât minus

șase împărțit la șase și obținem

x mai mic decât minus 6 împărțit

la 6 x mai mic decât minus 1 soluția

este formată din acele numere întregi

x cu proprietatea că x este mai

mic decât minus 1 a patra din ecuație

modul de x sau valoarea absolută

a lui x mai mică sau egală decât

4 Haideți să le prezentăm pe o

axă câteva numere întregi mai întâi

fixăm originea căreia îi asociem

numărul 0 și apoi o să punem în

ordine numerele 1 2 3 și 4 și opusele

lor minus 1 minus 2 minus 3 și

minus 4 să vedem care sunt numerele

întregi care au valoarea absolută

mai mică sau egală decât 4 mai

întâi observăm că numerele 0 1

2 3 și 4 verifica această inegalitate

deoarece toate au valoarea absolută

mai mică sau egală decât 4 valoarea

absolută a lui 4 este chiar 4 și

se verifică această inegalitate

dar observăm că și numărul minus

unu are valoarea absolută mai mică

sau egală decât patru de oarece

modul de minus 1 este unul la fel

modul de minus doi este doi Deci

minus doi verifica această inegalitate

același lucru se respectă și pentru

numerele minus trei și minus 4x

poate să ia valori între minus

patru și patru și atunci mă îmi

scrie minus 4 mai mic sau egal

decât x mai mic sau egal decât

4 soluția este mulțimea formată

din numerele întregi minus 4 minus

3 minus 2 minus 1 0 1 2 3 și 4

și ultima inecuația valoarea absolută

a lui x plus 2 mai mică sau egală

decât 3 Dacă în cazul anterior

x trebuia să fie cuprins între

minus patru și patru în acest caz

x plus doi trebuie să fie cuprins

între minus trei și tre să scriem

această inegalitate minus 3 mai

mic sau egal decât x plus 2 mai

mic sau egal decât 3 ca să obținem

numărul x între semnele inecuației

va trebui să scădem numărul 2 din

fiecare membru al acestei inecuații

și obține minus 3 minus 2 mai mic

sau egal decât x mai mic sau egal

decât 3 minus 2 minus 5 mai mic

sau egal decât x mai mic sau egal

decât 1 soluția este mulțimea formată

din numerele întregi minus 5 minus

4 minus 3 minus 2 minus 1 0 și

1
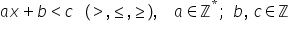
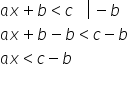
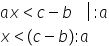
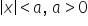
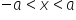