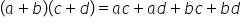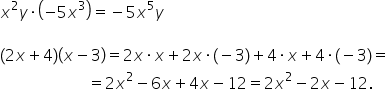Înmulțirea, împărțirea și ridicarea la putere a numerelor reale reprezentate prin litere

înmulțirea împărțirea și ridicarea

la putere a numerelor reale reprezentate

prin litere în calculele în care

avem de efectuat înmulțiri împărțiri

și ridicare la putere Am aplicat

regulile de calcul învățate până

acum iar pentru a desface parantezele

vor folosi distributivitatea înmulțirii

primul exercițiu minus 3x ori 2y

minus 3 ori 2 este minus 6x y doi

radical din doi la treia ori radical

din 2 la a doua știind că înmulțirea

este comutativă și atunci putem

să realizăm acești factori vom

scrie radical din 2 ori radical

din 2 la a treia la a doua radical

din 2 ori radical din 2 este 2

iar a treia pui a la a doua este

Ela cincea pentru că atunci când

înmulțim două puteri cu aceeași

bază exponenții se adună 3 x la

a doua ori minus 5x la a patra

mai folosi și aici comutativitatea

înmulțirii o să inversăm locu acestor

factori voi scrie minus 5 x la

a patra x la a doua Lidl coeficientul

se copiază x la a patra ori x la

a doua va fi x la a șasea și numărul

y se copiază 4 2a pe lângă 3-a

plus b numărul 2-a se va înmulțit

cu fiecare număr din paranteză

și Avem doi a ori 3-a plus doi

a ori b egal 2 ori 3 este 6-a ori

a este a la a doua pentru că exponenții

sunt unu și adunăm exponenții unu

plus unu este doi plus 2 ab 5 4x

la a doua totul ridicat la puterea

a doua plus exorex plus x împărțit

la x egal atunci când ridicăm un

produs la o putere se ridică fiecare

Factor la acea putere 4 la a doua

este 16 x la a doua totul la a

doua este x la a patra pentru că

înmulțim exponenții exorex va fi

x la a doua pentru că fiecare factori

are exponentul 1 și se adună exponenții

iar x împărțit la x este unul pentru

că întotdeauna atunci când împărțim

un număr la el însuși Rezultatul

este 1 în continuare Nu avem termeni

asemenea Deci rezultatul va rămâne

sub această formă 6 x la a 8-a

împărțit la x la a șaptea Plus

x la a 6-a împărțit la x la a cincea

o să scădem exponenții x la puterea

8 minus 7 va fi x la întâia adică

x Plus x la puterea 6 minus 5 la

fix la 1:00 x plus x este egal

cu 2x 7 x plus 4 pe lângă x minus

3 final pentru a desface parantezele

înmulțim primul număr din prima

paranteză cu fiecare număr din

a doua paranteză vom continua apoi

cu numărul 4 și îl înmulțim pe

rând cu fiecare număr din a doua

paranteză Așadar începem cu x și

avem x ori x plus x ori minus 3

plus patru ore x plus 4 ori minus

3 egal x ori x este x la a doua

x ori minus 3 este minus 3x plus

4x plus 4 ori minus 3 este minus

12 egal avem termenii asemenea

a minus 3x și plus 4x nu scrie

egal cu x la a doua minus 3 plus

4 este 1 adică x minus 12 8 2 radical

din 3 x totul la puterea a doua

împărțit la 3 x la a doua Nu bre

decat la pătrat Fiecare număr din

această paranteză 2 la a doua este

4 radical din 3 la a doua este

3 x la a doua împărțit la 3 x la

a doua egal 4 x 3 y este 12 x pătrat

împărțit la 3x pătrat 12 împărțit

la 3 este 4 x la a doua împărțit

la x la a doua este 1 Deci lăsăm

rezultatul 4 9 x la a doua minus

7x plus 5 minus paranteză x plus

opt pe lângă x minus 1 Nina până

la paranteză copiem fiindcă nu

avem termeni asemenea x la a doua

minus 7x plus 5 minus aici vom

de spațiu parantezele Dar pentru

că avem acest minus în față Voi

mai pune o paranteză rotundă urmând

Ca ulterior să schimbăm semnele

procedăm ca și la exercițiul numărul

7 înmulțim numărul x cu fiecare

număr din a doua paranteză apoi

numărul opt cu fiecare din a doua

paranteză și avem x ori x plus

x ori minus 1 plus 8x plus 8 ori

minus 1 egal x la a doua minus

7x plus 5 minus x la a doua x ori

minus 1 este minus x plus 8 x 8

ori minus 1 este minus 8 egal cu

x la a doua minus 7x plus 5 desfacem

paranteza schimbând semnele tuturor

termenilor din paranteză minus

x la a doua plus x minus 8x plus

8 egal x la a doua minus x la a

doua este 0 mai avem termeni asemenea

minus 7 x plus x minus 8 x minus

7 plus 1 este minus 6 iar minus

6 minus 8 este minus 14 x cinci

plus opt este 13 și ultimul exercițiu

minus 21 x la a treia plus 14 x

la a doua Alice 7x totul împărțit

la 7 x mai trebui să împărțim fiecare

termen din paranteză la 7 x Și

atunci vom scrie egal cu minus

21 x la a treia împărțit la 7 x

plus 14 x la a doua împărțit la

7 x plus 7 x împărțit la 7 x egal

minus 21 împărțit la 7 este minus

3 x la a treia împărțit la x este

x la a doua pentru că scădem exponenții

14 împărțit la 7 este 2 iar x la

a doua împărțit la x la întâia

va fi x iar 7 x împărțit la 7 x

este 1