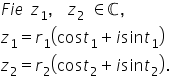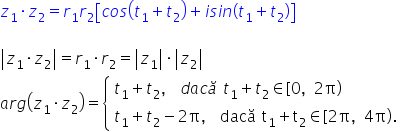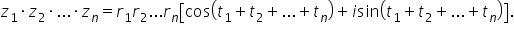Înmulțirea numerelor complexe
Tag-uri
Partajeaza in Google Classroom

Transcript
efectuarea operațiilor de adunare
și scădere a numerelor complexe
sub forma trigonometrică se realizează
ca și în cazul înscrierii acestora
sub forma algebrică mai exact se
adună respectiv se scad părțile
reale între ele și părțile imaginare
între ele însă operația de înmulțire
ridicare la putere sau extragerea
rădăcinii prezintă multiple avantaje
comparativ cu operațiile similare
în care numerele complexe sunt
exprimate algebric în acest videoclip
voi prezenta înmulțirea numerelor
complexe sub forma trigonometrica
pentru început aș vrea să reamintesc
forma trigonometrică a unui număr
complex 10 este egal cu aer pe
lângă cosinus de T plus sinus de
tir se numește raza polară și aceasta
Reprezintă modulul numărului complex
iar tei este argumentul redus iar
acesta este un unghi din intervalul
0 2 pi argumentul extins sau mulțimea
tuturor argumentelor numărului
complex sat este egal cu argumentul
redus plus doi capii unde k este
număr întreg și acum să vedem cum
înmulțim două numere complexe sub
forma trigonometrică avem numerele
Z1 de forma R 1 pe lângă cosinus
de T1 plus e sinus de 1 și z 2
egal cu a r 2 pe lângă cosinus
de 2 plus sinus de doi ne propunem
să calculăm produsul z12 mai întâi
îi vom înmulțim cele două module
R1 ori r2 și apoi înmulțim cele
două paranteze modul obișnuit obținem
astfel poze T1 ori cozi de 2 plus
cozi de 1 ori sinus de 2 plus sinus
de 1 cosinus de 2 plus sinus de
1 ori sinus de doi Dar e la pătrat
este minus 1 și din acest motiv
aici vom obține minus sinus de
1 sinus de 2 în continuare vom
separa aparte reală de cea imaginară
și avem R1 r2 pe lângă colț de
T1 cozi de Tedi minus scene de
T1 sin de T2 aceasta Reprezintă
formula pentru cosinus de T1 plus
te 2 apoi din următorii doi termeni
de factori comuni pe e și vom avea
cosinus de Teo nu sinus de 2 plus
sinus de 1 cosinus de 2 iar aceasta
este expresia pentru sinus de 1
plus te 2 am găsit astfel următoarea
formulă de calcul pentru produsul
a două numere complexe Z1 Z2 va
fi egal cu R1 r2 pe lângă cosinus
de 1 plus 2 plus e sinus de 1 plus
2 cu alte cuvinte cele două module
R1 si r2 se înmulțesc iar argumentele
reduse T1 și T2 se adună din această
relație de ducem că modul din Zetor
z 2 este egal cu R1 r2 dar R1 este
modulul numărului Z 1 iar r2 este
modulul lui z 2 obținem astfel
că modulul produsului zatt unul
Z2 este egal cu produsul modulelor
celor două numere argumentul redus
al produsului z12 se obține însumând
argumentele reduse T1 și T2 însă
trebuie să ținem cont de faptul
că și argumentul produsului trebuie
să fie un unghi din intervalul
0 2 pi Așadar această relație are
loc atâta timp cât te 1 plus te
2 face parte din intervalul 0 2
pi în cazul în care te 1 plus 2
este mai mare de 2 pini pentru
a obține argumentul redus al produsului
vom folosi următoarea relație argumentului
Z1 plus argumentului Z2 din care
scădem 2 pi vom folosi această
relație în cazul în care te 1 plus
2 aparține intervalului 2 pi 4
pi Așadar este important să reținem
că și argumentul redus al produsului
trebuie să fie un unghi din intervalul
0 2 pi dacă este mai mare decât
doi pini atunci în momentul în
care calculăm argumentul o să scădem
2 pi în ambele situații argumentul
extins al produsului sau Mulțimea
argumentelor este formată din argumentul
redus al numărului Z 1 plus argumentul
numărului z 2 plus 2 capii unde
k parcurge mulțimea numerelor întregi
Haideți să vedem în continuare
câteva exerciții Săcele să calculăm
produsul acestor două numere complexe
sub forma trigonometrică punând
în evidență modulul sau raza polară
și argumentul redus al produsului
pentru început înmulțim modulele
celor două numere vom avea a cinci
ore 210 pe lângă cosinus de 50
de grade plus 65 de grade așa cum
spuneam mai devreme adunăm argumentele
celor două numere plus e sinus
de 50 de grade plus 65 de grade
egal cu 10 pe lângă cosinus de
115 grade plus sinus de 115 grade
am obținut astfel că modulul este
egal cu 10 și argumentul redus
este egal cu 115 grade trecem la
punctul b avem din nou un produs
de două numere complexe exprimate
trigonometric mai întâi înmulțim
modulele 2 ori 36 pe lângă cosinus
de 175 plus 225 de de 400 plus
e sinus de 400 de grade Unghiul
de 400 de grade este mai mare decât
2 pi în consecință pentru a afla
argumentul redus al produsului
va trebui să scădem 360 de grade
obține astfel 6 pe lângă cosinus
de 400 minus 360 Plus e sinus de
400 minus 360 de grade egal cu
6 pe lângă cosinus de 40 de grade
plus sinus de 40 de grade modulul
este egal cu 6 iar argumentul redus
este unghiul de 40 de grade continuăm
cu punctul c avem din nou un produs
de două numere complexe m vom avea
2 radical din 3 supra 3 pe lângă
cosinus de pi supra 6 plus 2 pi
supra 3 plus e sinus de pi supra
6 plus 2 pi supra 3 egal cu 2 radical
din 3 supra 3 pe lângă amplificăm
a doua fracție cu doi ne dă patru
p plus p 5 p supra 6 plus e sinus
de 5 supra 6 modulul este egal
cu 2 radical din 3 supra 3 iar
argumentul redus este 5 supra 6
și un ultim exercițiu avem radical
din 2 ori radical din 6 este radical
din 12 adică 2 radical din 3 pe
lângă cosinus de 9 pi pe 4 plus
11 pi supra 12 plus e sinus de
9 pi pe 4 plus 11 pi pe 12 egal
cu 2 radical din 3 pe lângă amplificăm
cu 3 3 ori 9 27 plus 1138 pi supra
12 plus sinus de 38 pi supra 12
observăm că 38 supra 12 este mai
mare decât 2 pi Și atunci vom scrie
astfel 38 pi supra 12 se poate
scrie 24 pi pe 12 plus 14 pi pe
12 și egal cu 2 pi plus ai simplific
u27 pi supra șase am obținut astfel
egal cu 2 radical din 3 pe lângă
cosinus de 2 pi plus 7 pi supra
6 plus e sinus de 2pi plus 7 pi
supra 6 egal în continuare cu 2
radical din 3 pe lângă cosinus
de 7 pi supra 6 folosim Dino periodicitatea
funcțiilor lui sinus de 7 pi supra
6 modulul este 2 radical din 3
argumentul este 7pi supra 6