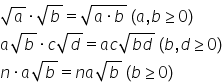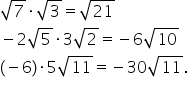Înmulțirea numerelor reale

prin înmulțirea a doua numere reale

a și b se obține un număr real

si notat cu aur b și numit produsul

numerelor a și b a și b se vor

numi factori înmulțirea numerelor

reale are următoarele proprietăți

asociativitatea acest lucru însemnând

că atunci când avem o operație

de înmulțire în care apar trei

factori putem să iasă ciem Cum

dorim iar rezultatul înmulțirii

nu se schimbă comutativitatea adică

putem să inversăm locul factorilor

numărul unu este element neutru

acest lucru însemnând că orice

număr real a înmulțit cu 1 va fi

el însuși și înmulțirea este distributivă

față de adunare și scădere adică

a apei lingă b plus c va fi egal

cu a ori b plus a ori c la fel

este și pentru scădere din această

ultimă proprietate vom de duce

următoarea proprietate și anume

atunci când avem o sumă de doi

termeni ce conțin același factori

acesta se poate da factor comun

mă face un exemplu în care vomă

evidențiat Ce este proprietăți

ne propunem să calculăm următorul

exercițiu 15 ori 0 ori 1 supra 5

minus 0 ori doi avem mai multe modalități

de a rezolva acest exercițiu Dar

ar fi de preferat să o alegem pe

cea mai ușoară folosind proprietățile

de mai sus mai întâi voi folosi

comutativitatea și voi inversat

locul factorilor din paranteză

și obținem 0 ori 15 ori 1 supra

5 minus 0 ori 2 acum folosim asociativitatea

și asociem acești doi factori 15

și 1 supra 5 Deci va fi egal cu

0 ori paranteză 15 ori 1 supra 5

minus 0 ori doi în paranteză putem

să simplificăm pe diagonală cu

515 împărțit la 5 este 3 5 împărțit

la 5 este 1 și avem 0 ori 3 minus

0 ori 2 observăm că 0 apare ca Factor

în fiecare din acești termeni și

atunci putem să dăm factor comun

pe 0 pe lângă 3 minus 2 care va

fi egal cu 0 ori 1 1 fiind element

neutru obține rezultatul 0 să vedem

la continuare Cum putem să înmulțim

Numerele care conțin radicali dar

de cal din x ori radical din y

avem următoarea convenție atunci

când înmulțim un număr cu radical

și un număr fără radical acesta

se scrie în fața radicalului de

exemplu radical din 3 ori 7 este

egal cu 7 radical din 3 iar minus

7 ori radical din 3 se va scrie

minus 7 radical din trei nume scrie

semnul înmulțirii în continuare

mă face câteva exerciții primul

exercițiu radical din 2 ori radical

din 3 va fi egal cu radical din

2 ori 3 egal cu radical din 6 2

minus radical din 7 ori minus 2

regula semnelor este aceeași ca

și la numerele raționale respectiv

ca și la numerele întregi minus

ori minus este plus iar numărul

2 se scrie în fața radicalului

rezultatul va fi 2 radical din

7 3 2 ori radical din 3 ori 5 folosind

comutativitatea înmulțirii și o

să schimbăm locul ultimilor doi

factori și obținem 2 ori 5 ori

radical din 3 2oo 5 este 10 radical

din 3 4 radical din 2 ori radical

din 8 va fi egal cu radical din

2 ori 8 Care este egal cu radical

din 16 atunci când avem pătrate

perfecte vom Calculați și radicalul

radical din 16 este egal cu 4 5

minus radical din 3 ori radical

din 3 este egal cu minus radical

din 3 ori 3 care este egal cu minus

radical din 9 iar radical din 9

este 3 6 5 ori radical din 2 ori

radical din 32 egal cu 5 ori radical

din 2 8 32 egal în continuare cu

5 radical din 64 dar de cal din

64 este 8 Scrie cinci ori opt Care

este egal cu 40 7 6 radical din

3 ori minus 5 radical din 2 nu

am înmulțit șase cu minus cinci

și obținem minus 30 și radical

din 3 ori radical din 2 este radical

din 6 8 minus 4 radical din 7 ori

minus 3 radical din 2 minus ori

minus va fi plus 4 ori 3 este 12

și radical din 7 ori radical din

2 este radical din 14 9 minus 4

radical din 2 ori 3 radical din

2 unui radical din 2 înmulțim mai

întâi primii doi radicali A minus

4 ori 3 este minus 12 medical din

2 ori radical din 2 este radical

din 4 cea mai rămas 2 radical din

2 observăm că 4 este pătrat perfect

și atunci extrage multi radicalul

și apoi vom efectua înmulțirea

obținem minus 12 ori 2 ori 2 radical

din 2 12 ori 4 este 48 Deci obținem

minus 48 radical din 2