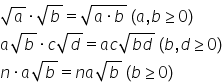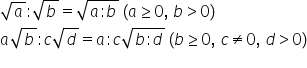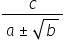Înmulțirea și împărțirea numerelor reale

să facem acum câteva exerciții

cu Înmulțirea și împărțirea numerelor

reale de forma c supra a plus radical

din b și a doua forma c supra a

minus radical din b și vom începe

cu acest exercițiu avem aici un

produs dintre două fracții 10 supra

radical din 3 și a doua fracție

radical din 12 supra 5 Cum înmulțim

două fracții foarte simplu numărători

între ei și numitorii între ei

însă mai înainte Ce trebuie să

vedem pe trebuie să observăm dacă

putem face sau nu vreo simplificare

și iată că aici putem simplifica

pe 10:05 prin cinci și obținem

1 și aici 2 Mai putem face vreo

simplificare sigur avem aici radical

din 3 și radical din 12 însă o

să scriu prima fracție mai să nu

încărcăm aici notația De ce avem

2 supra radical din 3 asta am obținut

înmulțit cu radical din 12 supra

1 acum fi puteți simplifica direct

prin radical din 3 aici obțineți

160 obține radical din 4 sau puteți

face astfel radical din 12 se scrie

pe 12 este 4 ori 3 trecând radicalul

peste produs avem radical din 4

înmulțit cu radical din 3 adică

2 radical din 3 Păi cum Aici Avem

chiar o să șterg 2 radical din

3 iată că putem simplifica foarte

ușor pe radical din 3 și radical

din 3 cu radical din 3 și obținem

aici 1:01 Deci rezultatul Cât este

Avem doi ori doi adică rezultatul

final este 4 sau dacă avem acest

exercițiu 1 supra radical din 5

împărțit la radical din 2 supra

18 Cum se scrie Cum calculăm de

fapt împărțirea a două fracții

împărțirea devine de fapt înmulțirea

dintre deîmpărțit Deci prima fracție

și inversul împărțitorului adică

inversăm numărătorul cu numitorul

și avem fracția 18 supra radical

din doi Bun Aici putem să facem

vreo simplificare Atunci trebuie

să înmulțim numărătorii între ei

și vom obține la numărător 18 și

numitori între ei adică radical

din 10 Acum putem să raționalizăm

amplificăm cu radical din 10 și

vom avea 18 radical din 10 supra

10 putem face chiar și o simplificare

pentru că aici avem 1860 a simplificăm

prin 2 și vom obține 18 împărțit

la 2 ne dă 9 radical din 10 10

împărțit la 2 ne dă cinci dar dacă

avem acest produs 1 supra radical

din 3 minus 2 înmulțit cu radical

din 15 minus 2 radical din 5 totul

supra 4 înainte de a face produsul

putem face vreo simplificare nu

avem nicio simplificare evidentă

însă observăm că aici avem radical

din 5 iar Aici avem radical din

15 pe care îl putem scrie radical

din 5 înmulțit cu radical din 3

Păi asta înseamnă că de fapt tem

să îl dăm factor comun la numărător

pe radical din 5 Da Și atunci Haideți

să copiem primul prima în avem

1 supra radical din 3 minus 2 înmulțit

cu 6 dăm factor comun pe radical

din 5 aici radical din 5 pe lângă

vom avea așa radical din 3 minus

2 închidem paranteza supra 4 poiată

Că fiind aici produs putem să facem

simplificarea simplificăm acest

număr Și acesta chiar prin această

diferență Deci aici o să Tăiem

la fel și acest umăr și o să ne

rămână unul și unul Deci rezultatul

Cât este avem la numărător radical

din 5 iar la numitor îl avem pe

patru dacă avem acest calcul 3

supra radical din 7 minus 1 înmulțit

cu 12 plus 6 radical din 5 supra

5 Păi nici aici nu avem vreo simplificare

evidentă în să observăm că putem

să dăm factor comun aici pe cât

pe 6 Iată avem aici 6 pe lângă

2 plus radical din 5 Păi Haideți

să rescriem de fapt să calculăm

acest produs cât vom obține la

numărător Păi avem 3 înmulțit cu

6 înmulțit cu 2 plus radical din

5 iar la numitor Haideți să scriem

acest radical din 5 așa iar la

numitor avem produsul 5 pe lângă

radical din 7 minus Păi ce putem

face în acest moment putem să amplificăm

să raționalizăm această fracție

adică vom amplifica cu chiar o

să schimb culoarea radical din

7 plus unu Da Și atunci vom avea

egal mai departe cu linie de fracție

ce vom obține Păi la numărător

vom avea trei ori 618 pe lângă

2 plus radical din 5 pe lângă radical

din 7 plus 1 iar la numitor avem

5 pe lângă radical din 7 la pătrat

minus 1 la pătrat și trebuie să

facem calculul care apare aici

în paranteză Deci vom avea copiem

numărătorul Ia să vedem Poate reușim

să îl chiar să îl copiem casă numai

rescriem bun Și aici vom avea 5

înmulțit cu 7 minus unu șase poiată

că acum putem să facem între adevărul

simplificare 18 și 6 prin șase

ne rămâne aici unu și aici ne rămâne

3 Deci rezultatul care va fi notăm

egal cu linie de fracție numitorul

îl scriem este cinci iar la numărător

Avem 3 pe lângă 2 plus radical

din 5 pe lângă radical din 7 plus

1 sigur putem să desfacem parantezele

să facem calculul sau nu e neapărat

nevoie dacă avem însă această împărțire

15 supra radical din 11 plus 2

împărțit la 3 supra radical din

11 minus 2 păi cum facem împărțirea

dintre două fracții împărțirea

a două fracții a de fapt înmulțirea

între prima fracție adică între

deîmpărțit pe care Haide să îl

copiem și inversul împărțitorului

Deci inversăm aici numărătorul

cu numitorul și vom avea radical

din 11 minus 2 supra 3 si simplificări

putem face Păi din start observăm

că putem simplifica 15 și 3 prin

3 obținem aici 165 însă mai putem

face vată simplificare că ia pe

aici avem aceleași numere radical

din 11 și doi la fel și aici însă

aici avem scădere între ele iar

Aici avem adunare între ele de

fapt aceste două numere sunt numere

iraționale diferite și atunci nu

ne rămâne decât să facem acest

produs și vom obține egal mai departe

cu avem linia de fracție cât obținem

la numărător Păi avem cinci pe

lângă radical din 11 minus 2 iar

la numitor avem această sumă radical

din 11 plus 2 și să ștergem linia

de fracție că e mult prea mare

în continuare Nu ne rămâne decât

să raționalizăm amplifica această

fracție acest raport cu cât cu

radical din 11 minus 2 daca la

numitor să obținem un număr rațional

și va fi egal cu la numărător vom

avea 5 pe lângă acest număr înmulțit

cu el însuși ne dă radical din

11 minus 2 la pătrat iar la numitor

avem radical din 11 la pătrat minus

2 la a doua și Haideți să facem

calculul trebuie să facem aceste

ridicări la putere Deci vom avea

5 pe lângă radical din 11 minus

2 la a doua și aici ne rămâne 11

minus patru Deci va fi egal mai

departe cu aici vom obține șapte

cum mai putem să calculăm numărătorul

Ce putem face la numărător Păi

trebuie să aducem la pătrat această

diferență atenție aceasta este

forma de scriere a acestui număr

irațional nu mai avem cum să restrânge

această diferență prin urmare cum

vom aduce acest număr la pătrat

Păi foarte simplu ne vom referi

ne vom folosi de această formulă

a minus b totul la pătrat este

egal cu a pătrat minus 2 a b plus

b pătrat Oricare ar fi a și b numere

reale Deci vom obține aici 5 pe

lângă radical din 11 la pătrat

minus doi înmulțit cu doi acest

2 ori radical din 11 plus 2 la

a doua și am închis paranteza prelungim

și linia de fracție și vom obține

vom avea aici 5 pe lângă aici obținem

11 minus 4 radical din 11 plus

4 Dar 2 la a doua totul supra 7

egal și vom scrie rezultatul final

numitorul 7 5 pe lângă 11 cu patru

15 minus 4 radical din 11 și de

abia acum sa încheiat calculul