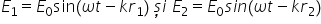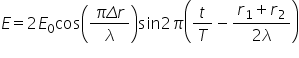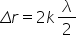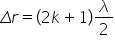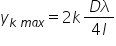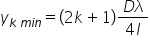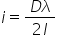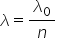Interferenţa luminii. Franjele interferenţei staţionare. Interferometrul Young.
Tag-uri
Partajeaza in Google Classroom

Transcript
în cele două lecții de optică ondulatorie
vom discuta despre fenomenul de
interferență a luminii și despre
dispozitivul Young să reamintim
întâi câteva noțiuni esențiale
în legătură cu fenomenul de interferență
despre care am discutat atunci
când am prezentat interfera interferența
undelor mecanice în primul rând
interferența este în general suprapunerea
a două unul și în particular interferența
luminii se referă la suprapunerea
a două radiații vizibile radiațiile
vizibile vă reamintesc sunt unde
electromagnetice cu lungimea de
undă în intervalul 400 de nanometri
700 Milano metri interferența este
staționară dacă cele două radiații
provin de la 200 coerent a sursei
coerente avem atunci când diferența
de faza dintre ele este o constantă
și în particular când pulsatiile
celor două Unde sunt egale atunci
ce formează așa numitele ventre
și noduri care sunt ficsi adică
nu se deplasează în timp ventrele
sunt locațiile în care amplitudinea
unde de interferență este maximă
și nodurile sunt locațiile în care
această amplitudinea este minimă
propagarea frontului unde se realizează
în conformitate cu principiul principiul
huygens din nou Am discutat despre
acest principiu în lecțiile despre
interferența undelor mecanice cea
mai importantă proprietate a interferenței
staționare este că intensitatea
luminoasă a unde rezultante de
interferență e constant în timp
în toate punctele Câmpului de interferență
aceasta deoarece intensitatea luminoasă
se definește ca energia electromagnetică
în unitatea de unitatea de suprafață
și timp și Deci se poate demonstra
plecând de la această definiție
noi nu facem această demonstrație
dar plec în această definiție se
poate demonstra că intensitatea
unde intru anumit punct deschis
de vectorul poziție aer și la un
anumit moment a este o constantă
înmulțită cu amputat amplitudinea
Unde în acea poziție și la acel
timp la pătrat ținând cont de această
ecuație și Ținând cont și de definiția
unde staționare și anume undă staționară
are amplitudini în punctele unde
independente de timp De ce amplitudinea
în propoziție aer la un moment
dat oarecare te este dependentă
numai de poziția aer și nu de timpul
în care ne uităm în această poziție
făcând uz de această proprietate
unde staționare rezultă imediat
că undele staționare în particular
undele staționare obținute prin
interferență a o intensitate luminoasă
si depinde numai de poziție nu
depinde de timp această intensitate
luminoasă în particular pentru
undă plană care a fost discutată
și ea în lecțiile de unde mecanice
un de plan este un da la o distanță
mare de sursă Deci pentru o undă
plană intensitatea luminoasă sa
demonstrat a fi egală cu 1 pe 2
înmulțită cu densitatea Metro pagare
viteza de propagare a undei pulsația
Unde la pătrat și amplitudinea
la pătrat având Deci în cazul la
Andi plane această constantă este
egală cu cu acest produs unul pe
doi rove Omega pătrat acestea au
fost noțiunile generale de interferență
cu aplicație în interferența lumii
Să considerăm acum două undă coerente
de aceeași altitudine reamintesc
că unde coerente înseamnă aceeași
pulsație și că aceeași pulsație
înseamnă același număr de undă
k dacă undele se propagă prin același
mediu aceasta deoarece ca numărul
de unde este definit ca doi pe
Lambda lungimea de undă Care este
egală cu produsul dintre viteza
de propagare și perioada t și din
definiția perioade acesta este
pulsația Omega împărțită la viteza
V Deci dacă cele două unde au aceeași
pulsație Omega și se propagă prin
același mediu ceea ce înseamnă
că au aceeași viteză de propagare
atunci le vor avea și același număr
de undă și Considerăm că cele două
unde au aceeași amplitudine pentru
că în aplicațiile practice felul
în care se obțin unde coerent Spre
exemplu după cum vom vedea prin
divizarea aceluiași unde Sau prin
reflexia unei unde rezultă că în
aplicațiile practice Vom avea în
majoritatea cazurilor aceeași am
pur și simplu adunăm aceste două
unt Deci on the rezultantă este
1 plus 2 care este zero înmulțit
cu sinus de 2pi timpul în perioada
te minus poziție RON împărțit la
alum de lungime de undă plus același
termen pentru cea de a doua undă
în care am folosit bineînțeles
definițiile pulsația Omega după
cum susțin definiție este 2 pi
supra și a undei de numărului de
undă ca care prinde ființe este
2 pi pe lemne pentru a aduna aceste
două funcții sinusoidale folosind
următoarea relație trigonometrică
sinus de Alfa plus sinus de beton
unde Alfa și Beta sunt două unghiuri
Care care este egal cu 2 cosinus
de alfamino subită împărțit la
2 înmulțit cu sinus mult cu sinus
de Alfa plus viata împărțit la
2 Deci vom aplica această Identitate
trigonometrică pentru a calcula
această sumă de sinusuri unde Alfa
bineînțeles este argumentul primului
sinus și bataie este argumentul
celui de al doilea și de ce obținem
următorul următoarea formulă e
va fi egal cu 2-a zero doi și în
acest doi doi zero cosinus de diferență
împărțit la 2 adică 2pi împărțit
la 2 acest împărțit la 2 înmulțit
cu diferența dintre cele două argumente
Deci te 1 împărțit la 3 minus 1
împărțit la am da minus de 1 împărțit
la 3 plus r2 împărțitor lemne minus
cel al doilea argument și apoi
sinus de 2pi împărțit la 2 de suma
celor două argumente adică acest
Factor acest termen sârbă că în
cosinus în argumentul funcției
cosinus partea temporală se simplifică
și obținem o dependență numai depozițiile
1 și iar 2 funcția sinus păstrând
partea temporală Deci obținem următoarea
ecuație pentru intensitatea i a
undei de interferență Deci e va
fi egal cu o valoare e zero maxim
Deci Maximul aceste am aceste Bond
de interferență care este definit
k20 cosinus de acest termen de
se observă că el va fi pi 2 cu
2 se simplifică fie înmulțit cu
r 2 minus se unul care este Delta
aer împărțit la la Ida și am ales
să notăm această funcție cu o anumită
mărime 0 maxim pentru că ea nu
depinde de timp De ce este amplitudinea
cu care este înmulțită partea dependentă
de timp Care va fi sinusul De ce
este sinus de 2pi numai simplifica
un cu doi pentru că obținem 2 în
în întru paranteze deci de exemplu
obținem 2 t supratemă are care
se simplifică cu acest 2-a minus
scuzați acesta ar trebui să fie
R1 aici Deci aceasta este 1 minus
1 plus 2 împărțit la la Anda și
avem acest Factor 2 de la acest
Doina Deci aceasta este ecuația
Andi rezultate din interferența
celor două unde coerente Dorina
Cum să studiem cazul în care obținem
așa numitele franj luminoase sau
frangi întunecate care sunt echivalentul
din optică a lor și nodurilor despre
care am discutat în cazul interferenței
undelor mecanice Deci se numește
flanșă luminoasă punct punctele
aflate în poziția Delta aer în
care obținem interferență prin
interferență vivamax in aceasta
înseamnă pur și simplu că amplitudinea
unde rezultante e Care este acest
examen are valoare maximă asta
înseamnă că cosinus de fetal tire
supraland dar trebuie să fie plus
minus 1 dec plus minus unu pentru
că cine interesează de fapt este
intensitatea Deci în aceste puncte
obținem intensitatea luminii maximă
iar după cum vă aduceți aminte
Am discutat acum câteva minute
intensitate este proporțională
cu pătratul lui a0 Maxim amplitudinii
la pătrat Deci datorită faptului
că avem pătrat obținem intensitate
maximă în franjuri luminoase atât
pentru valoarea plus 1 cât și minus
unu a acestui Cocean Deci rezultă
că aceste franjuri luminoase în
care intensitatea luminii rezultată
prin intervenții este maximă se
află în pozițiile în poziția sau
în pozițiile în care Delta R adică
r 2 minus seru nu este un multiplu
par de la Ida pe 2 deci cosinus
este plus minus 1 când argumentul
este plus minus fii pe doi și nu
cu ind obținem Delta l egal cu
2 k multiplu par de semiumed franjele
întunecate sunt opusul sunt punctele
sau locul geometric al punctelor
în care interferență este distructivă
adică intensitate esti minima Si
atunci Poziția lor va fi astfel
încât cosinus acest co sa nu să
fie 0 Deci intensitatea să fie
0 la fel cosinusul este 0 când
argumentul lui este un multiplu
de și obținem că Delta R este egal
cu doi ca plus unul am dat pe doi
de fapt am am greșit aici cosinus
de C cosinus de ar trebui să scriu
cosinus de un unghi tata să spunem
este zero atunci când tata este
plus minus pi pe 2 și multiplii
de pi pe 2 și cosinus de teta este
plus minus unu când teta este plus
minus și multiplii de pic să fac
când acestea înlocuire obținem
valorile lui Delta aer pentru care
franjele sunt luminoase sau întunecată
discutăm despre dispozitivul ia
dispozitivul Young obține unde
coerente prin divizarea luminii
monocromatice de la o fantă filiformă
de către alte două fante S1 și
S2 filiform și paralele între ele
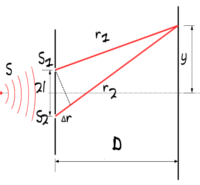
și cu schema ar fi următoarea avem
o sursă de lumină în fața îi punem
o fantă pentru a obține o sursă
punctiformă și bineînțeles din
această sursă vom obține propagarea
undelor de lumină la anumită distanță
în fața acestui fond de unde se
pun Două alte fante S1 și S2 foarte
mici la distanță mică între ele
și paralele vom obține că aceste
fante vor deveni și ele la rândul
lor surse secundare de lumină conform
principiului weekend și vom obține
În consecință două undă coerente
aceasta este partea cea mai important
deci andele secundare ce se propagă
din S1 și S2 vor fi coerente pentru
că provin din separarea cele și
unde deci vor avea aceeași pulsații
și ele se vor propaga la un moment
dat extinzând USA se vor întâlni
se vor suprapune generând fenomenul
de interferență care poate fi observat
pe un ecran e plasat la anumită
distanță Haideți să calculăm intensitatea
și condiția Ce rezultă din aceasta
intensitate condiția de interferență
maximală adică franjele luminoase
și respectiv interferență minimală
adică întunecate întru un punct
oarecare pe aflat la poziția sau
în în poziția de axa dispozitivului
notată prin această linie orizontală
întreruptă de este distanța dintre
planul surselor S1 S2 și ecranul
e putem scrie că 2 L Care este
distanța dintre cele două surse
atât 2 L De ce sună S2 cât și y
Alfa fiind acestui unghi este foarte
mic atunci putem Scrie următoarele
ecuații în primul rând tangent
de Alfa este egal cu y împărțit
la de pe de altă parte acest unghi
format în S1 între planul S1 S2
și perpendiculara din s1pe r2 De
ce aceasta este perpendiculară
acestui unghi este total fan deoarece
S1 S2 este perpendicular pe d e
prin definiție de asemeni ești
unul n este perpendicular pe OB
aproximativ perpendicular De ce
prin definiție sanu n este perpendicular
pe r2 adică pe s2p Deci nu pe o
pe dar în cazul în care punctul
b este foarte depărtat de planul
S1 S2 atunci Air 1 r2 și o p de
vin foarte apropiate între ele
acestui unghi devine foarte mic
și de și toate vor deveni R1 r2
și o p se identifică devin o singură
linie în aproximație a unui punct
pe foarte îndepărtat de sunet doi
și atunci s 1 an de vineri aproximativ
perpendicular pe toate aceste trei
linii de ce avem S1 n perpendicular
pe o pe aproximativ perpendicular
și atunci unghiul s2s 1 m este
egal cu unghiul Alfa ce putem scrie
că sinus de Alfa este activ egal
cu F2 n împărțit la 2 l Care este
sune S2 dar s2n este r 2 minus
zero unu adică Delta EUR s2n este
egal cu Delta Air în final putem
scrie că argumentul sau partea
dreaptă a acestei ecuații în părți
la de va fi egală cu partea dreaptă
a acestei ecuații Delta iar împărțit
la 2 L pentru că îmi pentru valori
foarte mici ale lui Alfa Deci pentru
Alfa tinde la 0 avem următoarele
ecuații sinus de Alfa aproximativ
egale cu alfa cosinus de Alfa este
aproximativ egale cu 1 și din acestea
doua rezultă că tangentă de Alfa
Care este definit ca sinus de Alfa
împărțit la coș de Alfa va fi și
el aproximativ egale cu el deci
putem scrie că împărțit la d este
aproximativ egale cu alfa și Delta
iar împărțit la 2 L este și el
egal aproximativ cu el rezultă
că y în părți de este egal cu Delta
l împărțit la 2 rezultă în concluzie
și în final că e y e poziția unui
punct p este egal cu d împărțit
la 2 înmulțit cu Delta EUR și acum
suntem gata să vedem când anume
se formează maxime și minime în
punctul P de la poziția y4 că ecuația
pe care o știm în cazul franjuri
luminoase este că diferența de
drum este o multiplu par de samian
Deci franjele luminoase se formează
atunci când acest Delta aer este
omul este 2k lanza pe doi Deci
e y în care valoarea lui y în care
se formează aceste maxime ale amplitudinii
Deci franjuri luminoase va fi un
multiplu car par de de orlanda
împărțit la 4 L la fel franjele
întunecate se formează în punctele
în care diferența de drum Delta
Air este un multiplu impar de semi
unde de la în Da pe 2 înlocuind
în această ecuație obținem ca Ce
este franzi întunecate în care
amplitudinea sau intensitatea mai
corect su si intensitatea este
minimă intensitatea este cea relevantă
în funcție de care de luminozitate
unde franjuri intensitatea luminoasă
Deci intensitatea este minimă în
punctele în care îndeplinesc condiția
a yourself raze luminoase sau întunecate
e același lucru ca diferența dintre
poziția Spre exemplu fragi luminoase
de ordinul ca plus unu și cea de
ordinul ca înlocuind obținem că
interfranja este dor Lambda împărțit
la 2 ultimul comentariu acest dispozitiv
de obicei se folosește în aer dacă
folosim alt mediu decât aerul atunci
singura modificare pe care trebuie
să o faci îmi este că lungimea
de undă trebuie împărțită la indexul
de indicele de refracție al meu