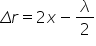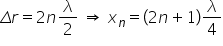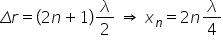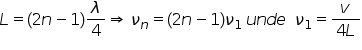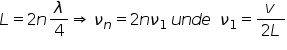Interferenţa prin reflexie. Unde mecanice staţionare.

în cea de a 11-a Lecție despre

oscilații și unde mecanice vom

discuta despre interferența prin

reflexie și despre undele staționare

interferența prin reflexie e cel

mai înalt Aurel mod și cel mai

simplu mă totodată de a obține

două unde coerente Spre exemplu

unele dintre o coarda elastică

întinsă despre care vom discuta

imediat spun cel mai natural și

simplu mod pentru că în acest caz

folosim o singură sursă de unde

și datorită faptului că interferență

are loc între o în de incidență

și unde ia reflectată obținem în

mod imediat o interferență a două

unul cu aer ante deoarece pulsația

unde incidente este egală cu pulsația

und reflectate Deci datorita acestui

interferența va fi automat staționară

și unde le produse vor fi staționare

un duel capătul corzii este fix

a unei corzi elastice întinse Deci

avem o reflecție cu pierdere de

simeon voi discuta pe scurt și

ce se întâmplă dacă capătul nu

este fix dar de obicei în aplicațiile

practice Elias de situația în care

ne găsim este următoarea avem o

coardă cu un capăt în care producem

perturbații inițială Deci sursa

inițială se află în acest capital

cu orz Unde se produce perturbatia

care se propagă sub forma unei

unde prin coarda aceasta până când

întâlnim capătul fix care nu se

poate mișca al corzii unde avem

o reflecție cu pierdere de semi

undă după cum am discutat în lac

trecut Deci avem o undă incidentă

iar la întâlnirea capătul xx a

legăturii obține o undă reflectată

Care este defazată cu 180 de grade

de acestei desenată așa avem de

unde faza și de 180 de grade sau

o pierdere de semiunda cele două

unde se propagă în sens contrar

Deci se vor întâlni fiind de aceeași

pulsație sunt coerente și vor genera

o undă staționară de interferență

în coardă Să considerăm un punct

pe aflat la o poziție oarecare

pe coardă și la distanța x de capătul

corzii dar semi notăm cu l lungimea

corzii atunci putem Scrie următoarele

ecuații x 1 care este distanța

parcursă de un de incidente până

în punctul P va fi egal cu lungimea

corzii minus poziția x a punctului

pe x 2 care este distanța parcursă

de un da reflectată Deci x-1 este

parcursă de un dai incidentă iar

X2 de un duh reflectată De ce x

2 este egal cu el plus x Care este

distanța totală parcursă de un

da reflectată dar după cum în sus

deoarece capătul cu orz este fix

avem o pierdere de semi un dar

de ce trebuie să ținem cont de

acest fapt scăzând din X2 un minus

Lambda pe doi să calculăm diferența

de drum dintre cele două undei

incidență și reflectată până în

punctul pe unde se întâlnesc Deci

Delta x care este x 2 minus x 1

prin definiție va fi mod Evident

egal cu 2x minus am dat pe 2 efectuăm

căderea după cum am văzut în lecția

trecută cunoaștem de așa condițiile

pe care un punct pe trebuie să

le îndeplinească din punctele de

la poziției sale pentru a se afla

pe o aventură sau pe un Note el

unde staționare pentru ventre avem

condiția ca diferența de drum față

de cele două sus În cazul nostru

față de undele incidență și reflectată

să fiu multiplu par de samian înlocuind

valoarea diferenței de drum Delta

x în această ecuație obținem că

x adică Poziția ventre lor da lungul

corzii este dată de următoarea

ecuație multiplu impar de sferturi

de un de asta înseamnă că ventrele

vor fi localizate în pozițiile

următoare x n este egal pentru

n un număr natural bineînțeles

Deci pentru n egal cu 0 obținem

la îndată 4 pentru n egal cu unu

obținem 3 la am dat pe 4 următorul

fiind 5 la am dat pe 4 și așa mai

departe de asemeni tot în lecția

trecută am de dus ecuația pentru

poziția nodul și anume nodurile

se află în poziția în care diferența

de drum este o multiplu impar de

seminte înlocuind iarăși ecuația

pentru diferența de drum În cazul

nostru obținem valorile pentru

x Deci x n care sunt pozițiile

nodurilor din undă staționară Da

lungul corzii sunt multiple pare

de sferturi de unt Deci nodurile

se vor afla în pozițiile xn 0 pentru

n egal cu 0 lemn de pe 2 pentru

n egal cu 1 și Lambda pentru n

egal cu 2 și așa mai departe pentru

n egal cu 3 3 lemne pe 2 și așa

mai departe ca și comentariu în

cazul reflexiv fără pierdere de

semn de adică în cazul particular

în care acest capăt nu este fixat

Ce este lăsat liber să oscileze

Atunci după cum spuneam nu mai

avem o pierdere de semiunda Deci

nu mai trebuie să scădem acest

minus lanate doi x doi va fi egal

cu el plus x și refăcând calculul

observăm că în acest caz ecuația

pentru ventre devine cea pentru

noduri adică ventil de vor fi localizat

ala multiple pare de sferturi de

undă și nodurile vor înlocui ventrele

deci pur și simplu ne coasele de

dus vom avea noduri în loc de ventre

și ventre în loc de noduri în acest

caz Deci dacă o coardă este supusă

unei astfel de perturbații cu coarda

elastică cu un capăt fix cu capăt

fix aici obținem următoarele unde

Următorul tip de unda în care bineînțeles

acești doi lobi sunt egali Deci

obținem noduri în pozițiile 0 lemn

de pe 2 și Lambda și așa mai departe

și ventre adică maxim în pozițiile

Lambda pe 4 și 3 lan de pe 4 aceastea

sunt pozițiile punctelor de maxime

și minime de a lungul axei o x

aleasă dealungul corzi bineînțeles

unde staționare Haideți să discutăm

proprietățile în general ale undelor

staționare între unde staționare

staționară toate ușile soarele

au amplitudini Constantin după

cum am discutat atât lecția trecută

cât și lecția aceasta poziții amplitudinea

unde lo staționare depinde doar

de Poziția lor în un de asta nu

înseamnă Bineînțeles că punctele

o și la toți avem o relație acorzi

doar amplitudinea valoarea maximă

elongații este constantă în timp

ceea ce face ca un da anvelopa

sa înfășurat Oare asa rămână constantă

în timp aplicațiile undelor staționare

sunt multiple instrumentele muzicale

care sunt diferite tipuri de instrumente

cu corzi instrumente cu tuburi

sau membrane cu corzi vioara chitară

și așa mai departe cu tuburi toate

instrumentele de suflat cu membrane

tobele și altele De asemenea acustică

a încăperilor și incintelor în

general de asemeni după cum am

discutat acum trei lecții undele

seismice de tip al undele seismice

lungi care sunt formate din interferența

undelor transversale și unde lor

longitudinale seismice sunt de

asemeni descrise de prin aceste

unde staționare de interferență

pentru formarea undelor staționare

lungimea mediului Care este cu

rdtube sau ce tip de mediu avem

trebuie să fiu multiplu de distanță

a distanței note pentru care este

un sfert de un de aceasta am discutat

în minutele precedente mai exact

dorim ca intru întruna astfel de

mediu cu Arda tube sau așa mai

departe să începem cu un un nod

să terminăm cu nod sau aventură

Sau invers să începem covor Trebuie

să termin cu note sau ventral Deci

Vrem ca la capetele mediului la

capetele corzii sau tuburilor să

avem ori noduri ori Venter să vedem

ce înseamnă această condiții și

anume ca lungimea mediului să fie

multiplu de distanța note pentru

adică la am dat pe patru în cazul

în care avem un capăt liber și

celălalt fix în ca vorbim despre

o coardă dacă vorbim despre un

tub bineînțeles asta înseamnă că

un capăt al tubului este deschis

și celălalt închis obține următoarele

ecuații înainte de a descrie cu

Vasile să notăm că această situație

se întâmplă Spre exemplu în instrumentul

numit Nike întruna y capetele în

care se suflă sunt deschise iar

capetele opuse sunt închise atunci

această condiție ca lungimea mediului

să fie o multiplu de distanță note

pentru înseamnă că lungimea tubului

sau acorzi dacă este văd dacă vorbim

despre o coardă este un multiplu

impar de sfert de unt folosind

relația de definiție a lungimii

de undă și anume lungimea de unde

este definită ca viteza de propagare

a undei în mediul respectiv înmulțită

cu perioada Unde putem scrie Columb

Da este egal cu Z împărțit la viteza

de propagare împărțită la frecvență

înlocuind Lambda cu această ecuație

schimb de peniu obținem frecvențele

25 ale Andi întru un astfel de

mediu cu capăt liber celălalt x

lungimea multiplu de distanța note

pentru și obținem aceste frecvențe

adică un multiplu impar de o frecvență

fundamental în unu care este definită

ca raportul dintre viteza de propagare

prin mediul V și de patru ori lungimea

în această se numește frecvența

fundamental observăm că lungimea

tuburilor dintre un Nai crește

întru anumită progresiei este aleasă

lungimea acestora tuburi este aleasă

încât fiecare din tub din din tuburile

naiului să corespundă unei anumite

frecvențe Deci suflând printrun

trup anume obținem anumite frecvențe

25 ale Andi produse în tub După

cum știți lungimi mai mari ale

tubului sau corzi mai lungi dacă

vorbim despre un instrument cu

coarde înseamnă frecvențe frecvența

lungimi mai mari înseamnă frecvențe

mai mici și lungimi mai mici tuburi

mai scurte sau cu ardei mai scurte

înseamnă frecvențe mai înalte ceea

ce se poate observa și experimenta

celălalt cealaltă situație este

în care ambele capete sunt libere

dacă nu avem acorzi sau deschise

dacă ne referim la tuburi sau ambele

capete Sunt fix dacă ne referim

acorzi sau închise dacă ne referim

la tuburi o astfel de situație

în întâlnim întru un instrument

numit țambal în care avem corzi

fixate la ambele capete în particular

fixate în cazul acesta și la mijloc

dar corzile sunt fixate la ambele

capete și atunci obținem următoarele

ecuații lungimea este un multiplu

par în cazul acesta de sferturi

de undă și la fel înlocuind lambda

lungimea de undă cu viteza de propagare

împărțită la nu obținem și ecuația

pentru frecvențele Nu produse care

sunt egale cu un multiplu par de

frecvența fundamentală nu unu la

fel dacă îți am balul are corzi

de lungimi diferite după cum are

și în acest caz țambalul are o

formă de evantai Deci lungimile

lungimea corzilor crește atunci

fiecare coardă va vibra la o frecvență

ce depinde de lungimea ei