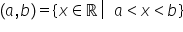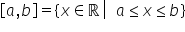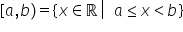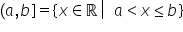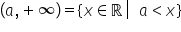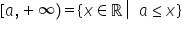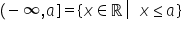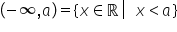Intervale mărginite și nemărginite de numere reale

Cu siguranță ați mai auzit cuvântul

interval în diferite contexte de

exemplu în intervalul de timp de

la 8:00 la 10:00 am lecție de tenis

asta înseamnă că de la ora 8 până

la ora 10:00 pe întreaga durată

a acestui interval de timp fac

tenis însă în această secvență

nu vom discuta despre intervale

de timp și despre intervale de

numere reale și avem aici o axă

a numerelor și vrem să găsim toate

numerele reale Deci x număr real

cu proprietatea că x este mai mare

sau egal cu 2 și mai mic sau egal

cu 3 acum ca să înțelegem mai bine

vom exprima geometric această relație

pentru că e o exprimare mai intuitivă

pentru aceasta considerăm punctul

A mare de 2 punctul b mare de coordonată

3 și vom reprezenta aceste două

puncte a și b iar pe axa numerelor

avem aici unitatea de măsură Deci

aici este numărul 1 numărul 2 este

aici trecem 2 punctul A mare de

coordonată 2 3 este aici 4 este

aici noi vrem să îl trecem pe 3

Deci la jumătatea distanței dintre

3 și 4 bun la întrecut aici 3 avem

punctul B acum noi vrem să găsim

toate numerele reale care sunt

situate între 2 și 3 cu altă cuvinte

vrem să găsim toate punctele și

tu care au coordonate 2 și 3 Deci

toate punctele situate între și

b Păi dacă Privim acest desen punctele

situate între a și b ce vom obține

Iată vom obține de fapt un segment

mai mult ca mine chiar un segment

închis segmentul închis a b bun

De ce se obține acest segment Păi

de nu se aude dreaptă știind că

axă a numerelor reale este în esență

o dreaptă dacă luăm pe o dreapta

două puncte de exemplu a și b atunci

oricâte apropiat ar fi cele două

puncte între ele Mai găsim un al

treilea punct de exemplu acesta

apoi între acest punct și punctul

A mai există încă un al treilea

punct care și el își mănâncă un

al patrulea de fac are și el este

între 2 și 3 și acest proces se

tot repetă și de fapt vom obține

o infinitate de puncte care au

coordonata între 2 și 3 și cum oricărui

punct care se află între a și b

îi corespunde o coordonată adică

un număr real situat între 2 și

3 înseamnă că vom obține de fapt

o infinitate de numere reale între

2 și 3 această mulțime reprezintă

de fapt un interval de numere reale

Cum îl notăm Păi fie înotăm geometric

Da Dar în general un interval de

numere reale îl notăm algebrică

astfel punctul a are coordonată

a2d și trecem 2 punctul b are coordonată

3 10 m punct și virgulă între coordonate

ca să le separăm și folosim aceeași

același timp de paranteze Deci

avem aici un interval închis 2

3 capetele intervalului sunt 2 și

3 virgulă cinci de ce El este un

interval închis pentru că Iată

x poate să ia și valoarea 2 și

valoarea 3 avem aici mai mic sau

egal la fel și aici mai mic sau

egal de fapt Orice număr real care

verifică această relație de pe

orice număr real x mai mare sau

egal cu 2 și mai mic sau egal cu

3 înseamnă că face parte din această

mulțime de ce echivalentă cu a

spune că x aparține acestei mulțimi

Haide să trecem mai sus să se vadă

clar bun Haideți să vedem acum

dacă numărul radical din 5 aparține

Oare acestui interval închis 2

3 Acesta este un interval mărginit

De ce spunem că este mărginit pentru

că îi cunoaștem marginile avem

aici numărul 2 și 3 m pentru a vedea

dacă radical din 5 aparține acestui

interval să folosim putem să folosim

o aproximarea lui radical din 5

și iată avem aici un calculator

dacă facem radical din 5 și am

obținut Aici este evidenta tu o

aproximare dacă vrem să îl aproxima

prin lipsă folosind două zecimale

obținem 2 radical din 5 a aproximativ

egale cu 2 și să vedem acum dacă

acest număr adică radical din 5

este mai mare sau egal cu 2 și

mai mic sau egal cu 3 și întradevăr

acest număr a cuprins între 2 și

3 Deci venim aici și Ștergem că

radical din 5 aparține acestui

interval Dar numărul 3 aparține

intervalului închis 2 3 Păi să vedem

dacă 3 49 pardon este mai mare sau

egal cu 2 și mai mic sau egal cu

3 este mai mare sau egal cu doi

și aici dacă vreți putem să mai

completăm cu o zecimală trecem

un zero nesemnificativ 3 este mai

mic sau egal cu 3 10 aparține acestui

interval Dar numărul 3 1 aparține

Oare intervalului închis 2 3 numărul

3 1 clari mai mare decât 2 însă

3 1 Cum este față de 3 pe aici avem

patru zecimale putem să completăm

cu încă trei zerouri nesemnificative

nu se schimbă cu nimic numărul

nostru și acum Haideți să comparăm

partea întreagă a gală cu partea

întreagă de aici prima zecimală

de aici egală cu de aici a doua

zecimală este egală cu a doua de

aici la fel și aceea de a treia

zecimală de aici egală cu aceasta

Însă a patra zecimală este mai

mare decât a patra zecimală de

aici Deci acest număr este strict

mai mare decât 3 Deci venim și stergem

ca acest număr dat nu aparține

acestui interval bun acum există

mai multe tipuri de intervale Următorul

tip de interval e dat de această

relație vrem să găsim toate numerele

reale x cu proprietatea că x este

mai mare strica doi și mai mic

strica 3 și am trecut aici pe axa

numerelor punctul a de coordonată

2 și b de coordonată 3 acum Care

sunt numerele reale strict mai

Marica 2 și strig mai mici ca 3

Păi dacă vom Reprezentați geometric

ce vom obține vom avea tot un segment

însă atenție avem acum un segment

deschis pentru că Iată x nu poate

să ia valoarea 2 asta înseamnă

că punctul A de coordonate 2 Nu

are ce să caute în această mulțime

la fel nici punctul B avem x este

strict mai mic ca 3 nu mai mic sau

egal cu Mera mai sus Deci am obținut

segmentul deschis a b la fel este

și intervalul nostru avem intervalul

deschis 2 3 este totul interval

mărginit Însă este interval deschis

pentru că numărul 2 nu aparține

acestei mulțimi chiar putem să

notăm Deci 2 nu aparține acestei

mulțimi la fel 3 nu apar ține acestui

interval deschis 2 3 dacă ni se

dă inegalitatea x mai mare sau

egal cu 2 și mai mic strict decât

3 când x este un număr real atunci

ce vom obține PA X poate să ia

și valoarea doi Dar nu poate să

ia și valoarea 3 de fapt avem tot

un segment însă pentru că aici

avem 2 mai mic sau egal cu x înseamnă

că vom avea un segment închis la

acest capăt și deschis la acesta

Pentru că x nu poate să ia valoarea

3 Deci avem acest segment închis

la a deschis la b și intervalul

este intervalul închis la acest

capăt și deschis la 3 Deci deschis

la dreapta putem să spunem că 2

aparține acestui interval însă

3 fiind un interval deschis la acest

capăt nu aparține intervalului

2 3 sau putem să avem această situație

în care Iată x este strict mai

mare ca 2 și mai mic sau egal cu

3 Și atunci vom obține un segment

deschis la acest capăt închis la

acesta Deci un interval deschis

la 2 și închis la 3 Evident cu aceste

condiții dacă avem acum această

din ecuație Deci vrem să găsim

toate numerele reale care sunt

mai mari sau egale cu 2 Păi ai

de să trecem aici și pe axa numerelor

punctul A mare de coordonată 2

Care sunt numerele mai mari sau

egale cu 2 Păi tot ce avem în această

parte axa numerelor reale și ce

obținem din punct de vedere geometric

Păi avem aici acest punct de la

care pornim și observăm că aici

nu avem nici o margine de fapt

obținem o semidreaptă Păi ca să

scriem semidreapta avem originea

în să mai avem nevoie de încă un

punct așa că Haideți să luăm aici

și vom avea numărul trei și aici

numărul 4 trecem punctul C de coordonate

4 și vom avea semidreapta AC cu

originea în A și acum cu Mix poate

să ia și valoarea A2 înseamnă Kapoor

a face parte din acest din această

semidreaptă Deci avem o semidreaptă

închisă banca să scriem intervalul

ne vom uita aici pe axa numerelor

Deci avem un interval închis la

stânga unde avem numărul 2 și ca

să arătăm faptul că avem acum atenție

un interval nemărginit în loc de

unul mărginit ca până acum aici

vom trece plus infinit Deci avem

intervalul închis la stânga 2 plus

infinit interval nemărginit Întotdeauna

când avem de a face cu acest simbol

semnul pe care îl vom trece va

fi o paranteză deschisă și atenție

plus infinit Nu este un număr real

Ce este un simbol pe care îl folosim

pentru a arăta nemărginirea dacă

avem acea situație Iată avem de

Determina toate numerele reale

care sunt strict mai mari ca 2

asta înseamnă că punctul A de coordonată

2 nu face parte din această mulțime

de ce avem o semidreaptă deschisă

în A și avem intervalul deschis

și nemărginit 2 plus infinit acum

dacă vrem să determinăm toate numerele

reale care sunt mai mici sau egale

cu doi ce vom obține Păi să trecem

punctul A de coordonată 2 pe axa

înainte de aceasta Haide să așezăm

tot si aici ceva mai sus bun și

am spus că vom trece punctul A

mare de coordonate 2 pe axa numerelor

care sunt numerele mai mici sau

egale cu 2 Păi vorbim De fapt de

aceste numere ia că care fac parte

din această zonă axa numerelor

numerelor reale ce obținem acum

Avem o semidreaptă închisă pentru

că Iată x poate să ia și valoare

a doi Deci punctul a face parte

din această semidreaptă o notăm

aici cu un ou originea axei numerelor

originea semidreptei Însă este

A deci avem semidreapta închisă

A8 Cum scriem acum intervalul Păi

dacă aici aveam plus infinit atunci

în partea stângă a avem minus infinit

și avem intervalul nemărginit minus

Infinit 2 aici trecem paranteză

rotundă când avem acest semn și

aici vând un interval închis la

dreapta a trece în paranteză pătrată

la fel minus infinit Haideți să

notăm aici nu este un număr real

al ne arată faptul că avem un interval

nemărginit intervin nemărginită

avem și în această situație în

care x este strict mai mic decât

doi singura diferență este că avem

acum o semidreaptă deschisă și

avem intervalul deschis în partea

dreaptă și nemărginit minus Infinit

2 Deci avem intervale nemărginite

Cum sunt aceste trei și haide să

îl vedem și pe cel dinainte Deci

intervale nemărginite corespunzătoare

unor semidrepte și intervale mărginite

Iată morfem istoric sample și încă

două exemple și ele sunt corespunzătoare

unor segmente Haideți să facem

acum două observații să facem prima

observație Deci notăm aici unu

dacă avem axei numerelor reale

Da putem să notăm aici minus infinit

așa cum am învățat și aici plus

infinit A bine mulțimea lor reale

poate fi scrisă și sub forma unui

interval și anume din intervalul

nemărginit minus infinit plus infinit

Deci mulțimea numerelor reale poate

fi scrisă și sub această formă

și a doua a observație este următoarea

orice interval este o submulțime

a lui R de exemplu intervalul minus

Infinit 2 este o mulțime de numere

reale și este o submulțime a mulțimii

numerelor reale sau un interval

mărginit cu mama avut să spunem

că avem un interval închis la stânga

și deschis la dreapta Deci intervalul

2 3 este tot așa o submulțime a

lui a ridici notăm este inclus

în mulțimea numerelor reale însă

nu orice submulțime a lui este

și interval de exemplu având aici

mulțimea A formată din elementele

1 și 2 este o submulțime a lui

R în săceanu tot aici nu este interval

ca să fie interval trebuia să avem

o altă notație care însemna că

în acea mulțime sunt toate numerele

reale cuprinse între unu și doi

însă cea notat aici reprezintă

o mulțime care are doar două elemente

și anume numerele 1 și 2