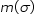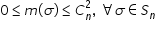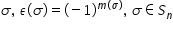Inversiunile unei permutări. Semnul unei permutări
Tag-uri
Partajeaza in Google Classroom

Transcript
știm deja că o permutare de gradient
este o funcție bijectivă Sigma
definită pe mulțimea A cu valori
în mulțimea A unde mulțimea A este
formată din elementele 1 2 n iar
Sen este mulțimea permutărilor
de grad n ne vom concentra în acest
videoclip asupra unui concept important
în studiul permutărilor și anume
paritatea unei permutări o utilizare
a acestui concept o Vom regăsi
în Definirea determinanților dar
este de mare ajutor în analiza
solvabilității unei probleme avem
următorul șir de numere 1 2 3 4
5 ce ne propunem să scrie aceste
numere în următoarea ordine 5 4
2 3 1 respectând următoarea regulă
Se pot schimba doar două numere
în același timp Cum vei proceda
am plecat de la șirul 1 2 3 4 5
voi schimba numărul 1 cu numărul
5 mai obține șirul 5 2 3 4 1 voi
schimba acum numărul 4 cu numărul
2 și obțin șirul 5 4 3 2 1 și mai
avem de făcut o singură schimbare
și anume pe 3 cu 2 obținând șirul
5 4 2 3 1 întreb dacă ai putea
obține șirul cerut Deci plecând
de la acest șir 1 2 3 4 5 să ajungi
la șirul 5 4 2 3 1 exact patru
schimbări sau dacă poți să faci
acest lucru în cinci schimbări
Taci Tot cu rezolvare a problemei
în secțiunea comentarii fie o permutare
Sigma de gradient iar i și j două
elemente ale mulțimii 1 2 n mai
mic decât z perechea Asia poartă
numele de inversiune a permutarii
Sigma dacă Sigma de e este mai
mare decât Sigma deja numărul acestor
perechi se notează cu m de sârmă
sunt Considerăm acum o permutare
de grad 4 care are reprezentarea
1 2 3 4 4 3 1 2 perechi a12 este
inversiune deoarece Sigma de unul
este 4 Sigma de 2 este 3 Deci Sigma
de 1 mai mare decât suma de 2 perechea
1 3 este și ea o inversiune pentru
că Sima de 1 este 4 iar Sigma de
3 este un segment de 1 mai mare
decât Sigma de 3 perechea 1 4 este
inversiune pentru că Sigma de unul
este 4 iar Sigma de 4 este egal
cu 2 Sigma de 1 m mai mare decât
suma de 4 perechea 2 3 este și
o inversiune pentru că Sigma de
2 este egal cu 3 iar Sigma de 3
este egal cu 1 Așadar Sigma de
2 este mai mare decât suma de 3
perechea 2 4 este inversiune pentru
că Sigma de 2 este egal cu 3 iar
Sigma de 4 este egal cu 2 Așadar
Sigma de 2 este mai mare decât
Sigma de 4 în total numărul inversiunilor
este așa cum vedeți cinci Deci
în această situație m de Sigma
este egal cu 5 Care credeți că
este permutarea cu numărul minim
de inversiuni pe nu poate fi vorba
decât de permutarea identică care
are reprezentarea 1 2 1 2 n pentru
această permutare numărul de inversiuni
este zero dar permutarea cu numărul
maxim de inversiuni Păi va fi acea
permutare Alfa Sonata în care elementelor
1 2 n le corespund aceleași elemente
dar în ordine descrescătoare Adică
n n minus 1 respectiv 1 să calculăm
numărul de inversiuni Păi elementul
1 formează cu toate celelalte elemente
inversiuni pentru că toate celelalte
imagini să mai mici decât n Deci
perechea 1 2 este inversiune ca
și perechea 1 3 ca și perechea
unui an adică în total avem n minus
1 inversiuni doi va face cu toate
elementele mai mari decât al inversiuni
adică avem perechile 2 3 2 4 respectiv
2 n obținem Așadar n minus 2 inversiuni
și așa mai departe ultima emisiune
este cea făcută de elementele n
minus unu respectiv N Deci ultima
inversiune este ieri minus unu
e Adică o inversiune Ce sumă am
aceste inversiuni Deci eu de Sigma
este egal cu n minus 1 plus n minus
2 plus puncte puncte plus sun Păi
regăsim în această sumă suma lui
Gauss și în concluzie m de sârmă
este in minus 1 înmulțit cu consecutivul
lui adică el totul supra 2 Păi
rezultatul acesta nu reprezintă
altceva decât combinari de n luate
câte 2 ce am obținut am obținut
că numărul de inversiuni poate
să ia valoarea minimă 0 sau valoarea
maximă combinari de n luate câte
2 adică 0 este mai mic sau egal
decât m de sârmă Care e mai mic
sau egal decât combinari de n luate
câte 2 oricare ar fi Sigma o permutare
de grade Ian cu ajutorul noțiunii
de inversiune vom defini noțiunea
de semn sau ce natură a unei permutări
fie Sigma permutare de grădi numim
semnul sau signatura permutarii
Sigma numărul epsilon de Sigma
egal cu minus 1 totul la puterea
M de Sigma o permutare se numește
o permutare pară dacă ții natura
este egală cu 1 iar permutarea
Sigma se numește permutare impară
dacă si natura este egală cu minus
1 Să considerăm acum permutarea
Sigma de gradul al patrulea 1 2
3 4 imaginile 4 3 1 2 este exemplul
precedent ne amintim că m de Sigma
la am de terminat ca fiind egal
cu 5 dar să le vedem aceste lucruri
avem versiunea 1 2 1 3 1 4 2 3
și 2 4 3 4 nu formează o inversiune
atunci epsilon de Sigma este egal
cu minus 1 totul la puterea a cincea
adică minus unu și în concluzie
permutarea Sigma este o permutare
impar Dacă vom considera acum o
permutare Delta cu reprezentarea
1 2 3 4 1 4 2 3 numărul de inversiuni
Luca coulomb astfel 1 nu formează
inversiune cu nici un element cu
niciun alt element pentru că toate
imaginile sunt mai mari decât 1
2 Formează două inversiuni 2 cu
3 respectiv 2 cu 4 3 de asemenea
nu formează inversiune cu patru
pentru că 2 este mai mic decât
3 epsilon de Delta este egal cu
minus 1 totul la puterea a doua
adică 1 Deci Delta este o permutare
pară am văzut că permutarea identică
a 0 inversiuni signatura permutarii
identice este minus 1 la puterea
zero Adică 1 permutare identică
este o permutare pară Dar oare
transpoziția Ce paritate are avea
Păi dacă vom considera o transpoziție
Asia cu cântarea 1 2 minus 1 e
e plus 1 k j minus 1 j n cu imaginile
1 2 imns 1j e plus 1 k j minus
unu e en Niciunul dintre elementele
de la 1 până la minus 1 nu formează
inversiune cu elementele mai mari
decât ele cum e este mai mic decât
z obținem că e va forma inversiune
cu toate elementele e plus unu
până la j inclusiv Deci avem inversiunile
e e plus unu e e plus doi e k e
r minus unu E J numărul acestora
inversiuni este egal cu j minus
de asemenea elementele e plus 1
până la Z minus 1 inclusiv vor
forma inversiuni cu elementul z
adică mai avem inversiunile e plus
1 J e plus 2 j iar ultimul ar fi
j minus 1 j în total aceste inversiuni
sunt în număr de j minus minus
1 adică numărul de inversiuni al
acestei transpozitii este j minus
plus minus minus 1 adică 2 pe lângă
z minus de nu sunt signatura transpoziție
a i j este minus 1 la puterea M
de Sigma adică minus unu Deoarece
m de Sigma este un număr impar
orice transpoziție Este o permutare
impară

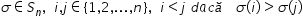
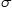 se notează
se notează