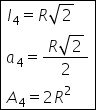Latura, apotema și aria pătratului (teorie)
Tag-uri
Partajeaza in Google Classroom
Transcript
în această lecție o să vedem Care
sunt formulele de calcul pentru
latura apotema și aria unui pătrat
în funcție de raza cercului circumscris
pătratului pornind de la aceste
formule pe care le am de dus într
o lecție anterioară referitoare
la un poligon cu n laturi am determinat
atunci formula de calcul pentru
latura apotema și aria unui poligon
în general an este numărul de laturi
ale Poligonului în cazul pătratului
N este 4 și atunci latura pătratului
va fi egală cu 2 r ori sinus de
180 de grade supra 4 egal cu 2
ori sinus de 45 de grade egal cu
2 r ori radical din 2 supra 2 se
simplifică 2 și obținem R radical
din 2 deci latura pătratului este
raza ori radical din 2 apotema
pătratului este r ori cosinus de
180 de grade supra 4 egal cu r
ori cosinus de 45 de grade egal
cu r ori radical din 2 supra 2
și egal cu raza radical din 2 supra
2 aria pătratului este patru ori
iar la a doua ori sinus de 180
de grade supra 4 ori cosinus de
180 de grade supra 4 egal cu 4
m la a doua ori sinus de 45 Care
este radical din 2 pe 2 ori radical
din 2 pe 2 egal 2 ori 2 este 4
și se simplifică cu 4 de la numărător
dar de cal din 2 ori radical din
2 este doi Deci obținem 2 iar la
a doua aria pătratului va fi 2
ore raza la a doua dacă dorim să
exprimăm aria pătratului în funcție
de latura știm deja această formulă
este latura la pătrat în cazul
în care dorim să calculăm perimetrul
pătratului înmulțim latura pătratului
cu patru Deci perimetrul pătratului
va fi patru ori latura egal cu
4 ori raza radical din 2 în cazul
în care dorim să calculăm latura
și apotema pătratului funcție de
raza cercului circumscris și nu
reținem aceste formule de la care
am pornit mai există și o altă
metodă de a calcula putem să aplicăm
de exemplu teorema lui Pitagora
În triunghiul dreptunghic ABD și
obținem o relație între latura
pătratului și raza cercului circumscris
aceste segmente b o a o d o și
c o a sunt roz iar o m este apotema
pătratului Aplicând teorema lui
Pitagora În triunghiul dreptunghic
ABD a b la pătrat plus a de la
pătrat este egal cu BD la pătrat
AB și AD sunt laturi Deci n la
a doua plus l la a doua este egal
cu bd ipotenuza este formată din
două raze b 8 plus OD și atunci
Putem să scriem 2r totul la pătrat
2 L la a doua este egal cu 4 r
la a doua împărțim la doi și obținem
ca la tura la a doua este egală
cu 2 ori raza la pătrat latura
va fi egal cu radical din 2 la
a doua Latura este raza radical
din 2 Evident am obținut aceeași
formulă ca și mai devreme în continuare
o să calculăm apotema pătratului
în funcție de raza cercului circumscris
observăm că om este linie mijlocie
în triunghiul bdc și atunci om
va fi jumătate din lungimea laturii
pătratului Deci apotema este latura
supra 2 și egal cu radical din
2 supra 2 aceasta va fi formula
de calcul pentru apotema pătratului
în funcție de raza cercului iar
aria va fi bineînțeles latura la
a doua egal cu radical din 2 totul
la a doua și egal cu 2 iar pătrat
aceasta este formula de calcul
a ariei în funcție de raza cercului
în continuare o să facem o problemă
Calculați latura apotema și aria
unui pătrat înscris în același
cerc cu un triunghi echilateral
de arie 27 radical din 3 centimetri
pătrați pentru a calcula latura
apotema și aria pătratului mai
întâi trebuie să calculăm raza
cercului circumscris având în vedere
că în același cerc este înscris
și un triunghi echilateral și știm
aria acestuia putem să determinăm
raza cercului circumscris Aplicând
formula de calcul pentru aria triunghiului
echilateral A3 adică aria triunghiului
ia sta trei ori raza la a doua
radical din 3 supra 4 și aceasta
este egală cu 27 radical din 3
din această relație o să exprimăm
raza înmulțim pe diagonală 3ar
la a doua radical din 3 egal cu
4 ori 27 radical din 3 împărțit
la radical din 3 și obținem fraier
la a doua egal cu 4 ori 27 împărțim
relația la trei Earl a doua egal
cu 4 ori 27 supra 3 se simplifică
27 cu 3 și obținem 9 e la pătrat
este patru ori 936 raza este egală
cu 6 cm am de terminat lungimea
razei cercului circumscris pătratului
putem să calculăm acum latura pătratului
L4 este raza radical din 2 egal
cu 6 radical din 2 apotema pătratului
este raza radical din 2 supra 2
egal cu 6 radical din 2 supra 2
și egal cu 3 radical din 2 aria
pătratului este în 2 ori raza la
a doua sau latura la a doua egal
cu 2 ori 6 la a doua egal cu 2
ori 36 egal cu 72 cm pătrați
Latura, apotema și aria pătratului în funcție de raza cercului circumscris pătratuluiAscunde teorie X
Navigare în lectii
Cumpara abonament
