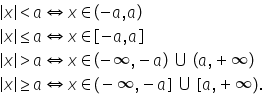Legătura dintre intervale și modul

să vedem acum Care este legătura

dintre intervale și modul și avem

acest exemplu vrem să găsim toate

numerele reale care au proprietatea

că modulul ori este mai mic sau

egal cu 3 și ne vom ajuta și de

axa numerelor reale am de prezentat

aici și unitatea de măsură Deci

vrem să găsim toate numerele reale

x astfel încât modul de x să fie

mai mic sau egal cu 3 în primul

rând Ce înseamnă modul de x y dacă

x este un număr real Să considerăm

că x este poziționat aici atunci

modul de x înseamnă distanța de

la origine până la punctul de coordonată

x adică această distanță distanța

aceasta Reprezintă modul de x acum

noi vrem să găsim acele numere

astfel încât această distanță să

fie cum mai mică sau egală cu 3

adică mai mică sau egală cu trei

unități de măsură pe Haide să ștergem

aici și să vedem dacă găsim un

număr care verifică întradevăr

această inecuația modul de 3 este

mai mic sau egal cu 3 sigur modul

de 3 ne dă 3 verifica această inegalitate

atunci Haideți să trecem pe 3 pe

axa numerelor avem aici unu doi

și aici este numărul 3 bun modul

de 3 în reprezintă chiar această

distanță Da avem aici modul de

trei adică trei unități de măsură

mai sunt și alte numere care verifică

această inecuatie Păi dacă luăm

de exemplu un număr situat între

0 și 3 să spunem că luăm acest

număr modulul său reprezintă distanța

de la origine până la acest punct

adică această distanță Cum este

față de 3 unități de măsură pe

această distanță este clar mai

mică decât trei unități de măsură

pe care ia tare Putem reprezenta

aici aici avem trei unități de

măsură asta înseamnă că de fapt

și acest număr verifică această

in ecuație bun dar de fapt Orice

număr am lua un număr cuprins între

0 și 3 o să verifice această in

ecuație pentru că modulul său va

fi mai mic sau cel mult egale cu

trei unități de măsură asta înseamnă

că Haideți să notăm fa mai repede

putem să ștergem aici toate numerele

care sunt cuprinse între 0 și 3

verifică inecuația dată sunt ele

singure Păi nu același lucru se

întâmplă și cu un simetricele acestor

puncte față de originea axei numerelor

dacă luăm numărul minus 3 Aici

este minus 1 minus 2 minus 3 modul

de minus 3 este mai mic sau egal

cu 3 modul de minus 3 ne dă Chiar

trei adică aceste trei unități

de măsură Asta înseamnă modul de

minus 3 pe orice număr am lua cuprins

între minus trei și zero de exemplu

acesta modulul sau va fi această

distanță dacă are Este clar mai

mică decât 3 unități de măsură

Deci orice număr am luat cuprins

între minus trei și zero va avea

modulul mai mic sau cel mult egale

cu trei unități de măsură deci

putem să notăm că toate numerele

care sunt cu între minus trei și

zero verifică și ele această in

ecuație sunt ele singurele dacă

luăm de exemplu un număr mai mare

strict decât 3 să spunem un număr

de aici Cum este modulul său Păi

modulul său înseamnă distanța de

la origine la acest punct o so

trasez cu galben cariată această

distanță cum este este mai mare

de trei unități de măsură deci

putem să notăm că nici un număr

mai mare sau mai mare strică A3

Nu verifică această in ecuație

deci aici nu avem soluții la fel

dacă luăm un număr strict mai mic

decât minus 3 de exemplu acesta

modulul său adică această distanță

va fi mai mare decât trei unități

de măsură Deci Nici aici nu avem

nici o soluție cu alte cuvinte

singurele numere care verifică

această in ecuație sunt cele cuprinse

între minus trei și trei cu minus

trei și trei inclusiv pentru că

vedem că și trei și minus 3 verifică

ce am obținut avem de fapt un interval

închis și Haideți să notăm că modul

de x este mai mic sau egal cu 3

dacă și numai dacă x aparține acestui

interval închis minus trei și trei

dacă avem acum vrem să găsim acum

toate numerele reale care au proprietatea

că modulul lor este strict mai

mic decât 4 mai devreme si ne apare

aici numărul 4 Haideți să trecem

și pe axa numerelor avem aici numărul

1 aici la avem pe 2 Aici este 3

și aici avem numărul 4 să vedem

acum dacă numărul 4 verifică această

in ecuație Adică dacă x este 4

modul de 4 este mai mic strict

decât 4 modul de 4 înseamnă de

fapt numărul 4 avem cu alte cuvinte

aceste patru unități de măsură

Păi clar nu este strig mai mic

decât 4 Deci avem aici o relație

falsă bună însă Orice număr am

lua Care este strict mai mic decât

4 și este cuprins între 0 și 4

va verifica piatră dacă luăm un

număr situat aici modulul acestui

număr chiar putem să îl trasăm

Iată este această distanță Care

clarii este mai mică decât patru

unități de măsură sau putem să

luăm un număr mai aproape de zero

De exemplu aici Păi modulul acestui

nu este această distanță care și

ea este mai mică strict decât patru

unități de măsură cu alte cuvinte

Orice număr am luat Care este cuprins

între 0 și 4 verifică această inecuației

însă Atenție nu îl punem în calcul

și pe patru da modul de 4 nu este

strig mai mic decât 4 Haide să

ștergem și aici sunt acestea singurele

numere nu la fel se întâmplă și

cu simetricele acestor puncte față

de originea axei numerelor dacă

luăm numărul minus 4 avem aici

minus 1 minus 2 minus 3 și minus

4 Păi nici numărul minus 4 nu verifică

pentru că modul de minus 4 nu este

strict mai mic decât 4 această

relație este falsă modul de minus

4 ne dă chiar patru însă ce număr

am luat cuprins între minus patru

și zero de exemplu acesta va avea

modulul mai mic decât patru unități

de măsură Deci toate numerele de

faptă numere cuprinse între minus

patru și zero vor avea modulul

strig mai mic decât patru unități

de măsură de și verifică această

in ecuație însă cum am spus nu

luăm în calcul numerele minus patru

și patru dacă luăm însă un număr

mai mare strict decât 4 Exemplu

un număr de aici Cum este modulul

său modulul său dacă e să îl și

Reprezentăm Iată trece de patru

unități de măsură Orice număr am

luat și acel număr să fie strict

mai mare decât 4 el va avea modulul

mai mare ca patru unități de măsură

Deci nu verifică această ecuație

mult Haide să hașură ma atunci

astăzi Dună pentru că aici nu avem

soluții la fel Nici aici nu avem

soluție este aceeași explicație

și ce am obținut Păi de fapt singurele

numere care verifică această inecuației

sunt cele cuprinse între minus

patru și patru fără să luăm în

calcul aceste două numere Deci

am obținut un interval deschis

notăm că modul de x este strict

mai mic decât patru Dacă și numai

dacă x aparține intervalului deschis

minus patru patru Acum putem să

își concluzionăm dacă avem o mulțime

care formată din elementele x numere

reale cu proprietatea că modul

de x este mai mic strict decât

ei Unde punem condiția ca ei să

fie un număr real a street mai

mare ca 0 pentru că modulul este

întotdeauna un număr mai mare sau

egal cu 0 Deci am luat a strict

pozitiv si vom obține Păi privind

acest text templu aici am obținut

minus patru patru interval deschis

Cum avea intervalul deschis în

minus a a dacă însă avem prima

situație adică x număr real cu

proprietatea că modul de x este

mai mic sau egal cu a atunci vom

obține un interval închis minus

a a dacă avem însă de Determina

toate numerele reale x astfel încât

modul de x este mai mare sau egal

cu doi Deci masa găsim toate numerele

reale care au modulul mai mare

sau egal cu doi Păi ia să vedem

numărul 2 verifică această inecuații

adică modul de 2 este mai mare

sau egal cu 2 figure modul de 2

ne dă chiar doi deci putem să îl

trecem pe axa pe doi aici este

Aici este numărul 2 iar numărul

2 verifică aceasta inecuației numărul

unu însă dacă x este egal cu 1

modul de 1 este mai mare sau egal

cu doi nu este modul de 1 reprezintă

această distanță care clar este

mai mică decât două unități de

măsură Deci aici avem o relație

falsă și putem să ștergem aici

unul nu este soluție pentru această

in ecuație noi vrem să găsim acele

numere care au modulul mai mare

sau egal cu două unități de măsură

dacă vrem ca modulul lor să fie

mai mare decât aceste două unități

de măsură unde vom căuta numerele

respective Păi divan căuta după

doi de exemplu acest număr are

modulul Iată Reprezentăm aici această

distanță este modulul său clar

mai mare decât două unități de

măsură de fapt toate numerele care

sunt mai mari ca 2 verifica această

ecuație pentru că cu cât ne îndepărtăm

mai mult de doi cu atât Ne îndepărtăm

și de zero și atunci aceste distanțe

vor crește or fi din ce în ce mai

mari și toate sunt mai mari decât

două unități de măsură Deci Toate

aceste numere de la 2:00 încolo

verifică inecuația dată am văzut

că un număr de aici Cum a fost

și numărul 1 are modulul mai mic

decât două unități de măsură Deci

nici un număr de aici nu va verifica

această in ecuație 1001 verifică

modul de 0 nu este mai mare sau

egal cu doi bani sunt acestea singurele

numere nu același lucru se întâmplă

și cu simetricele acestor puncte

față de originea axei numerelor

dacă avem numărul minus doi avem

aici minus 1 Aici este minus 2

modul de minus 2 și el este mai

mare sau egal cu doi pentru că

ne dă doi și la fel se întâmplă

cu orice număr mai mic strict decât

minus 2 de exemplu pentru acest

număr modulul său este această

distanță care clar este mai mare

decât două unități de măsură Deci

orice număr mai mic sau egal cu

minus 2 verifica această relație

însă aici nu avem nicio soluție

ce am obținut Pa iată că am obținut

de fapt două intervale intervalul

minus infinit minus 2 și intervalul

2 plus infinit Haideți să notăm

Deci avem intervalul nemărginit

minus infinit minus 2 și cum vom

trece la minus 2 minus 2 verifică

Deci avem de fapt un interval închis

aici la fel și aici deci a minus

infinit minus 2 și intervalul 2

plus infinit numerele din acest

interval adică de aici verifică

inecuația la fel și aceste numere

adică cele care sunt aici Cum scriem

atunci soluția Păi fiind mulțimi

de numere reale putem să le reunim

asta înseamnă că modul de x este

mai mare sau egal cu doi dacă și

numai dacă x aparține acestei mulțimi

la fel se întâmplă și dacă avem

inecuația modul de x 3 mai mare

decât 1 tot așa să determinăm toate

numerele de ale cu această proprietate

singura diferență este aceea că

în loc de mai mare sau egal avem

strict mai mare și evident și numărul

însă diferența importantă este

aceasta Cave mai strig mai mare

în loc de mai mare sau egal ce

vom obține aici vom obține o reuniune

de intervale nemărginite acum însă

deschise în minus 1 și 1 Deci modul

de x este mai mare ca 1 dacă și

numai dacă x aparține intervalului

nemărginit minus infinit minus

1 reunit cu intervalul 1 infinit

explicația este aceeași ca și în

exercițiul anterior dacă e să generalizăm

atunci dacă x este un număr real

cu proprietatea că modul de x este

mai mare strica atunci vom obține

de fapt această reuniune de intervale

minus infinit minus A reunit cu

a plus infinit atenție când a este

un număr real a scrii mai mare

ca 0 dacă avem însă De determinat

mulțimea formată din elementele

x numere reale cu proprietatea

că modul de x este mai mare sau

egal cu a atunci vom cine intervalul

minus infinit minus a închis aici

reunit cu intervalul a plus infinit

închis la ei mai facem acum două

scurte observații nu avem observații

sunt mai multe niște exerciții

Primul vrem să găsim x număr real

de faptul numerele reale care au

proprietatea că modulul lor este

mai mic strict decât minus 1 Păi

ce numere reale au modulul mai

mic strict ca minus spălați puțin

timp să vă gândiți Păi cum este

modulul unui număr real este mai

mare sau egal cu 0 atunci e posibil

ca un număr să fie în același timp

și mai mare sau egal cu 0 dar și

mai mic ca minus unu nu deci de

fapt aici nu avem soluții putem

să notăm că rezultă că x aparține

cine mulțimii vide deci întotdeauna

un modul nu are cum să fie steag

mai mic sau chiar putem să trecem

mai mic sau egal decât un număr

negativ al doilea exercițiu să

găsim acum x număr real a astfel

încât modulul său să nu fie mai

mic sau egal cu minus 1 și mai

mare sau egal cu minus unu Păi

cum este modulul unui număr real

Am scris mai sus mai mare sau egal

cu 0 Ce înseamnă asta că orice

număr real am trece noi în locul

lui x si vom obține aici va fi

un număr mai mare sau egal cu 0

Deci automat el va fi mai mare

sau egal cu minus 1 asta înseamnă

că toate numerele reale verifica

această inecuației deci putem să

notăm că rezultă că soluția este

dată chiar de mulțimea numerelor

reale