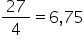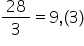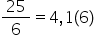Legătura dintre numitorul unei fracții ordinare ireductibile și numărul zecimal obținut

Vrem să vedem acum Care este legătura

dintre numitorul unei fracții ordinare

ireductibile și numărul zecimală

obținut atunci când transformăm

o fracție ordinară într o fracție

zecimală putem să ne dăm seama

de la început Ce fel de număr vom

obține nici măcar nu e nevoie să

facem împărțirea de aceeași acest

timp de exercițiu Iată se dau niște

fracții și fără să le transformăm

des fără să facem împărțirile să

determinăm acele fracții care reprezintă

fractii zecimale finite zecimale

periodice simple și zecimale periodice

mixte A păi Ia să vedem care sunt

regulile și vom începe cu acest

exemplu 18 supra 5 vrem să scriem

această fracție ordinară ca fracție

zecimală mai întâi verificăm dacă

fracția ordinară dată este o fracție

reductibilă Deci acesta este primul

pas aducem fracția dată dacă nu

este deja la o fracție ireductibilă

noi avem deja nu mai poate fi simplificată

atunci nu ne rămâne decât să împărțim

pe 18 la 5:00 Haideți să facem

rapid împărțirea bun 5 intră în

18 de 3 ori 3 ori 5 ne dă 15 obținem

aici 3 acum trebuie să coborâm

acele trebuie să coborâm primul

0 nesemnificativ Păi nu mai e nevoie

să trecem neapărat virgula Și acel

zero însă în momentul în care am

trecut un zero aici trebuie să

punem virgula la cât 30 împărțit

la 5 Nan de 6 ori 5 30 iar dacă

împărțirea sa încheiat am obținut

3 sau un alt exemplu 27 supra 4

înseamnă 27 împărțit la 4 din 9

mai întâi verificăm dacă avem o

fracție și intră adevăr Avem așa

ceva 4 se împarte la 227 nu se

împarte la 2 un număr impar deci

putem să facem liniștiți împărțirea

27 împărțit la patru avem aici

6 6 x 4 24 și obținem restul 3

întotdeauna atenției destul pe

care îl obținem trebuie să fie

mai mic decât împărțitorul așa

putem mereu să verificăm că împărțirea

pe care o face o fată este una

a făcută corect pun acum coborâm

0 Deci trebuie să treci în virgula

la cât 30 împărțit la 4 7 7 ori

4 ne dă 28 iar obținem aici restul

2 2 iar și este mai mic ca 4 coborâm

0 20 împărțit la 4 ne dă cinci

ori 420 și se încheie 8 am obținut

6 și putem să luăm și alte templu

dacă am face 27 Haideți la un tot

cu 27 supra 10 numărul pe care

îl vom obține va fi 2 de fapt regula

este următoarea dacă numitorul

Deci dacă numitorul unei fracții

atenție ireductibile conține sau

este alcătuit doar din puteri ale

lui 5 sau 2 atunci rezultatul pe

care îl vom obține va fi o fracție

zecimală finită Toate aceste fracții

zecimale sunt finite Iată care

sunt numitorii noștri pe prima

dată am avut numitorul 5 a doua

oră am avut numitorul 4 care se

scrie 2 ori 2 apoi am avut 10 care

se scrie 2 ori 5 Dacă am avea de

exemplu o altă fracție cu numitorul

50 Aflați ireductibilă atunci ai

de să trecem aici 1131 atunci rezultatul

pe care îl vom obține va fi sigur

o fracție zecimală finită pentru

că numărul 50 numitorul Cum se

scrie este 2 ori 25 adică 2 ori

5 ori 5 cu alte cuvinte dacă la

o fracție ireductibilă numitorul

este alcătuită doar din factorii

2 și 5 respectiv puteri ale lui

doi și ale lui 5 atunci rezultatul

pe care îl vom obține va fi un

număr zecimal finit dacă avem însă

această situație și avem fracția

28 supra 3 din nou Verifică dacă

fracția ordinară dată este una

ireductibilă aici avem 28 nu se

împarte exact la 3 Deci avem o

fracție ireductibilă Deci facem

împărțirea a 28 împărțit la 3 și

Haideți să împărțim și 8 împărțit

la 3 avem nouă ori 3 ne dă 27 obținem

aici restul unu coborâm acuma 0

asta înseamnă că la cât vom trece

virgula 10 împărțit la 3 de 3 ori

3 ori 3 ne dă 9 obținem 1 iar își

coborâm 10 împărțit la 3 tot 3

3 ori 3 ne dă nouă din 9 obținem

1 mai departe vom trece vom coborî

zero vom obține din nou 3 iarăși

1 și așa mai departe Deci Rezultatul

este 9 Deci venim și notăm 9 sau

alt exemplu 25 împărțit la 9 Deci

25 împărțit la 9 este o aceasta

o fracție ireductibilă Da cât vom

avea dacă facem împărțirea rezultatul

va fi 2 sau un alt exemplu Ion ține

pe care am făcut o întru altă secvență

video 47 supra 21 facem împărțirea

și Aceasta este o fracție ireductibilă

21 are ca factorii pe 3 și 7 47

nu se împarte exact la 3 nici la

7:00 și vom obține acest număr

Avem doi virgulă și în perioada

a avem cifrele doi trei opt zero

nouă cinci Deci avem 2 38.000 95

Ce observăm peste tot am obținut

fracții zecimale periodice atenție

simple observăm Da Toate sunt periodice

simple A bine regula este următoarea

atunci când avem o fracție ordinară

ireductibilă dacă numitorul A nu

conține nicio putere a lui 2 și

nicio putere a lui 5 atunci rezultatul

va fi o fracție zecimală periodică

simplă Păi ce numitori Am avut

Am avut aici numitorul 3 am avut

aici numitorul 9 care se scrie

trei ori trei am avut aici numitorul

21 care se scrie trei ori șapte

Păi pe nicăieri nu ne apărut factorul

2 sau vreo putere a lui 2 Evident

diferită de 2 la 0 sau vreo putere

a lui 5 tot așa diferită de cinci

la zero în asemenea situații vom

obține o fracție zecimală periodică

simplă Dacă avem însă acest caz

și voi lăsa aici cuvântul ireductibilă

pentru că dacă mi se dă tot așa

o fracție ireductibilă de exemplu

25 supra 6 și această ireductibilă

atunci când facem împărțirea să

vedem ce vom obține 25 împărțit

șase avem patru ore 624 obținem

aici restul unu coborâm 0 Deci

trebuie cinci virgulă la cât Zece

împărțit la 6 o dată unul 6 6 obținem

aici 4 coborând 0 40 împărțit la

6 este 6 6 ori 6 36 și obținem

aici 4 din nou trebuie să trecem

0 din nou vom avea e66 X6 tot așa

36 din nou 4 și așa mai departe

Deci rezultatul va fi 4 perioadă

6 Ce fel de fracție am obținut

aici avem o fracție zecimală periodică

atenție mixtă Cum este numitorul

numitorul 6 se scrie 2 ori 3 De

ce regula este următoarea dacă

la o fracție ireductibilă numitorul

conține pe lângă alți factori factorii

2 sau 5 atunci rezultatul va fi

o fracție zecimală periodică mixtă

cu alte cuvinte regulile sunt următoarele

dacă numitorul unei fracții ireductibile

conține doar puteri ale lui 2 sau

5 atunci vom obține o fracție zecimală

finită dacă însă nu conține nicio

putere a lui 2 și nici o putere

a lui 5 atunci vom avea o fracție

zecimală periodică simplă Deci

conține numitorul conține alți

factori însă nu conține puteri

ale lui 2 Evident diferite de 2

la 0 și puteri ale lui 5 diferite

de 5 la 0 atunci cum avea o fracție

zecimală periodică simplă Dacă

avem însă o combinație adică numitorul

conține pe lângă alți factori și

vreo putere a lui 2 sau a lui 5

atunci vom avea o fracție zecimală

periodică mixtă și acum Haide să

ne Revenim la primul exercițiu

nici să dau acestei cinci fracții

ordinare și fără să facem împărțirile

Vrem să vedem care dintre ele reprezintă

fracții zecimale finite sau zecimale

periodice simple sau mixte Deci

mai întâi Ce trebuie să facem trebuie

să verificăm pentru fiecare fracție

în parte dacă avem o fracție ireductibilă

după ce am făcut acest lucru ne

vom uita la numitor 3 supra 2 este

ireductibilă Cum este numitorul

Păi numitorul este format doar

din numărul doi Deci o mulțime

o fracție zecimală finită trecem

aici 3 supra 2 17 pe șase tot așa

este o fracție ireductibilă Cum

îl scriem pe 6 pe 6 se scrie în

doi ori trei deci iată că suntem

în la ultima regulă adică pe lângă

alți factori pe lângă factorul

3 în pare și factorul 2 asta înseamnă

că vom obține o fracție zecimală

periodică mixtă 17 pe 611 pe 25

din 9 este o fracție ireductibilă

25 Cum se scrie Din ce factori

este alcătuit numărul 25 Păi avem

cinci ori cinci e bine o fracție

al cărei numitor conține doar puteri

ale lui 2 sau 5 va deveni o fracție

zecimală finită Deci venim aici

și notăm 11 supra 25 12 supra 77

și aici avem o fracție ireductibilă

77 Cum se scrie Păi se împarte

exact la 7 și avem șapte ori 11

iată că în această scriere nu ne

apar facto puteri ale lui 2 sau

5 factorii 2 și 5 luni afara aici

Asta înseamnă că vom avea Ce fel

de fracție zecimală periodică simplă

Deci venim și notăm 12 supra 77

și în final 28 pe 15 este tot așa

ireductibilă 15 se scrie 3 ori

5 iar dacă pe lângă factorul 3

ne apare factorul 5 Deci avem o

combinație Deci ne încadrăm în

ultima regulă vom avea o fracție

zecimală periodică mixtă 28 supra

15 și cu aceasta am încheiat