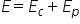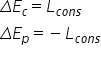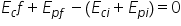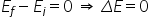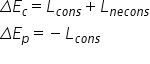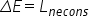Legea conservării energiei mecanice. Exemple de aplicare.
Tag-uri
Partajeaza in Google Classroom

Transcript
în cea de a patra Lecție despre
legi de conservare în mecanică
vom discuta despre legea de conservare
a energiei mecanice să începem
prin a defini energia mecanică
energia mecanică este energia totală
a sistemului adică este suma dintre
energia cinetică și energia potențială
pentru a exemplifica cu un sistem
simplu Să considerăm sistemul format
din pământ și un corp Aflați anumit
înălțimea h și care are o viteză
oarecare V Dar care viteză este
măsurată în sistemul de referință
terestru adică față de Pământ acest
corp bineînțeles se va afla sub
influența forței de greutate G
în acest caz energia mecanică a
sistemului va fi egală cu suma
dintre energia cinetică adică mv
pătrat pe 2 și energia potențială
adică m g h și această energie
după cum vom vedea se conservă
ecuațiile pentru energia cinetică
și energia potențială gravitațională
în acest caz sau fost de dus în
lecția trecută legea conservării
energiei mecanice spune că această
energie mecanică a unui sistem
izolat în care acționează forțe
conservative e constantă adică
se conservă Deci spunem că legea
mecanică constantă sau că variația
este 0 elementele importante ale
acestei legi sunt subliniate și
primul este că sistemul trebuie
să fie izolat adică să nu există
forțe externe dacă există forțe
interne și dacă avem în energie
potențială asta înseamnă că există
forțe interne ele sunt konservative
în acest caz Spre exemplu avem
o forță și anume forța gravitațională
dar ea este o forță internă adică
acționează între cele două componente
ale sistemului corpul și pământul
și este o forță conservativă definiția
forțelor konservative a fost dată
în prima lecție de legi de conservare
mecanică o prima consecință a acestei
legi de conservare este următoarea
fie două stări ale sistemului de
la momentele T1 și T2 energia mecanică
se conservă înseamnă că suma dintre
energia cinetică și energia potențială
la omentul te unu este egală cu
aceeași sumă evaluată la momentul
T2 aceasta înseamnă că diferența
dintre energia cinetică la cele
două momente este egală cu minus
aceeași diferență a energiei potențiale
momentele t1 t2 și dau Deci variației
energiei cinetice este egală și
de semn opus variației energiei
potențiale acest lucru îl cunoaștem
intuitiv din experiența noastră
cotidiană Spre exemplu luăm un
sistem simplu format din un ciocan
și un cui la momentul inițial ciocanul
se află în repaus și sub acțiunea
greutății forță de greutate Deci
El are o energie potențială datorită
forței de greutate dacă este lăsat
liber atunci el va avea o viteză
diferită de zero să transformăm
o parte din această energie potențială
întro energie cinetică corespunzătoare
acestei viteze nenule în momentul
în care ciocanul ajunge în contact
cu un Cuiul atunci el se oprește
Deci viteza devin egale cu 0 și
Deci avem iarăși în caz în care
energia cinetică de vine zero camera
în momentul inițial dar această
variație de la ING cineticii de
la mp pătrat la zero se transformă
într o energie potențială care
generează o forță asupra cu Deci
avem un caz în care transformăm
energia potențială cinetică și
înapoi cinetică în potențial Ce
se întâmplă dacă totuși există
forțe externe neconservative dacă
asupra sistemului acționează forță
neconservative externe care au
rezultată rezultantă f Deci Suma
vectorială a acestor forțe externe
neconservative Atunci după cum
am văzut în lecția precedentă variației
energiei mecanice va rețeta ta
este egală cu lucrul mecanic al
acestor forțe Deci energia mecanică
nu se mai conservă Delta e nu mai
este egal cu zero un exemplu de
forță ne conservativă este frecarea
cu aerul să dăm un exemplu de conservare
a energiei și anume căderea liberă
a unui corp Deci avem același sistem
pământ și un corp corpul se află
la înălțimea h întru un punct A
și bineînțeles se află sub acțiunea
forței de gravitație de gravitație
în momentul Terrier el ajunge în
punctul B aflat la o înălțime h0
înălțimea HCL și H2O în punctul
b și în final ajunge în punctul
C pe suprafața pământului deoarece
singura forță care acționează asupra
corpului este cea de greutate care
este o forță internă între corp
și pământ și conservativă atunci
energia totală mecanică se conservă
Deci energia în punctul a este
egală cu energia în punctul b este
egală cu energia în punctul C și
cu energia din orice punct dar
în traiectorii aceasta înseamnă
că mgh pentru că în punctul A avem
numai în Egipt inițială corpul
se află în repaus va fi egal cu
m v b pătrat împărțit la 2 plus
m g h d care este egal cu m v c
pătrat împărțit la doi în punctul
c avem numai energie cinetică după
cum spuneam dacă luăm în considerare
Și faptul că în căderea lui corpul
dezvolta o forță de frecare cu
aerul De ce există un al treilea
sistem și anume aerul prin care
corpul se mișca atunci în timpul
mișcării vom avea o forță de frecare
iar această forță de frecare este
o forță neconservative În consecință
în acest caz nu mai putem scrie
aceste aceste ecuații ci mai degrabă
că variația in a a mecanice totale
este egală cu lucrul mecanic al
acestei forțe de frecare cu aerul
Spre exemplu a b în punctul b minus
energia în punctul a se va scrie
ca minus forța de frecare înmulțită
cu minus HD reamintesc lucrul mecanic
al forțelor rezistive este negativ
de aceea semnului so luăm un alt
exemplu aruncarea pe orizontală
al unui obiect a unui obiect Deci
avem un corp un obiect pe care
îl aruncăm Deci imprimăm imprimăm
o viteză orizontală b 0 care este
paralelă cu suprafața pământului
și el va avea bineînțeles o traiectorie
de cădere până va atinge pământul
aceasta este viteza finariu are
două componente V X și vei notăm
cu A punctul inițial și cu b punctul
final alegem un sistem de coordonate
bidimensional o x y și notăm cu
h înălțimea de la care aruncăm
obiect Deci să folosim conservarea
energiei mecanice în această aruncare
pe orizontală care se tot o aruncare
liberă Pentru că Considerăm numai
efectul greutății ce putem scrie
că energia totală din punctul a
este egală cu energia mecanică
totală în punctul B Deci mv 0 pătrat
împărțit la 2 plus m g h este egal
cu m z pătrat împărțit la doi deci
putem scoate ecuația pentru modulul
vitezei la sol de pătrat este egal
cu 0 pătrat plus 2 g h adică V
este egal cu radical din 0 pătrat
plus 2 g h direcția vitezei la
ajungerea la sol este dată de la
punctul B adică este dată de unghiul
Alfa Deci pentru a specifica complet
viteza la în punctul B Trebuie
să găsim atât modul cât și direcția
adică unghiul Alfa iar unghiul
Alfa este dat de următoarea ecuație
tangentă de Alfa este egal cu y
pe vei Deci prin definiție vei
x este perpendicular pe vre ca
asta înseamnă că tangent de Alfa
este egal cu cateta opusă Vega
împărțit la cateta alăturată v
x z x este foarte ușor de calculat
pentru că mișcarea pe orizontală
pe axa o x este uniformă singura
accelerație din sistem este gem
și este vertical G este accelerația
gravitațională care egal cu greutatea
împărțită la masă și acționează
numai pe o y b ci vei x va fi egal
cu vedea din nou pentru că pe axa
x nu avem nicio accelerație dar
în același timp viteza totală la
pătrat este prin definiție egală
cu x pătrat plus y y y pătrat rezultă
că vezi 0 pătrați plus 2 g h este
egal cu 0 pătrat plus y y pătrați
Deci vei ys3d cu radical din 2
c h Deci tangentă de Alfa care
de Direcția vitezei în momentul
atingerii solului este radical
din 2 g h supra z 0 Deci Am calculat
atât modulul cât și orientarea
vitezei în momentul în care corpul
atinge