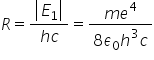Legea seriilor spectrale în modelul Bohr.

în cea de a opta lecții de fizică

atomică vom discuta despre spectrele

atomului de hidrogen în lecțiile

trecute am dezvoltată modelul Atomic

a lui bohr și am început să discutăm

despre primele aplicații practice

ale lui Spre exemplu în calculul

energiei de ionizare a atomului

de hidrogen dorind să vedem în

această lecție dacă modelul vor

poate explica rezultatele experimentale

obținute în în studiile asupra

aspectelor atomului de hidrogen

Deci primul lucru pe care dorim

să le reamintim rapid este ceea

ce am discutat în prima lecție

de fizică atomică și anume rezultatele

experimentale în legătură cu aspectele

de emisie atomice care sunt spectrele

de linii ce respectă așa numita

lege a seriilor spectrale Care

este următoarea 1 pe Lambda de

cinci versuri lungimii de undă

a radiației emisă de un atom în

cazul acesta de hidrogen este egal

cu Constanța rydberg care are această

valoare înmulțită cu 1 pe n1 la

pătratul Unde în unul este numărul

serii spectrale minus 1 pe 2 la

pătrat unde N2 este numărul liniei

din seria spectrală respectivă

Deci în doi trebuie să fie mai

mare decât în unu și atunci această

mărime este pozitiv definită am

discutat despre Toate aceste lucruri

și despre seriile spectrale particulare

ce se pot obține în prima lecție

de fizică atomică un comentariu

acestă mărime și anume inversul

lungimii de undă se mai numește

și număr de 1 2 și se notează cu

nu tilda vom introduce în curând

această notație Deci ne propune

un această lecție să vedem dacă

putem explica aceste rezultate

experimentale folosind modelul

bohr În primul rând să reamintim

postulatul al doilea arbore care

spune că o linie din spectrul de

emisie de linii al atomului de

hidrogen corespunde unei frecvențe

de tranziție între două stări staționare

am modificat un pic formularea

dar este însă postulatul lui bohr

este aceasta scrisă matematică

asta înseamnă că frecvența radiației

mi sa vorbim despre aspecte de

emisie în cazul acesta de frecvența

radiației de emisie va fi egală

cu diferența dintre energia stării

staționare inițiale și cea a Stării

staționare finale împărțită la

Constanța planck h folosind legătura

dintre lungimea de undă și frecvent

sunt și anume aici lungimea de

undă a unei radiații este prin

definiție gală cu viteza de propagare

Care este viteza în fiind mulți

viteza luminii în vid înmulțită

cu perioada unde a Deci avem Lambda

egal cu c împărțit la frecvență

Deci înlocuind frecvența cu lungimea

de unde În această formulă obținem

că inversul lungimii de undă emise

de către un atom de hidrogen în

tranziția între o stare inițială

și o stare finală are această valoare

a minus e f împărțit la HC unde

din nou a este energia stării staționare

inițiale și ef este energia stări

staționare finale iar h e f este

energia fotonului emis în această

tranziție atomului modelul bohr

Care este dezvoltat plecat plecând

de la postulatele vor modelul bohr

ne dăm o valoare precisă a acestei

energii și anume În cazul acesta

cele două stări staționare corespund

la două nivele energetice cu numerele

cuantice principale și în acest

caz zici mai exact putem scrie

formulele pentru aceste două energii

și ele sunt următoarele energia

stării staționare inițiale este

e 1 împărțit la n e pătrat unde

n este numărul cu anticipa al al

stării inițiale și respectiv energia

stării staționare finale efpa fie

1 împărțit la n f la pătrat și

unul este energia stării fundamentale

care corespunde numărul cuantic

principal n egal cu 1 și are această

valoare după cum am discutat în

lecțiile trecut deja putem vedea

cât obținem o coincidență a formule

pentru numărul de undă obținute

experimental de se vede că experimental

obținem un număr de unde egal cu

o constantă înmulțită cu diferența

dintre două inverse de pătrate

de numere întregi de acest 1 pe

an 1 la pătrat minus 1 pe 2 la

pătrat aceasta este rezultatul

experimental iar modelul bordești

teoria ne spune că acest invers

de lungime de unda va fi întradevăr

egal cu o contră care vom vedea

imediat Cât este dar înmulțită

cu diferența dintre două invers

de pătrate de numere întregi De

ce intră adevăr putem vedea de

la joacă modelul board scrie foarte

bine rezultatul experimenta Haideți

să vedem mai concret Ce rezultă

din această comparație între teorie

și experiment Deci după cum am

spus introducem așa numit un număr

de undă Care este frecvența nu

canti la deasupra și este egală

cu raportul dintre secvență și

viteza luminii în vid Care este

de asemenea Gal după cum o arătat

cu inversul lungimii de undă Deci

modelul bohr de următoare alege

că numărul de undă este egal este

egal cu valoarea absolută a lui

E unul care este energia stării

fundamentale împărțită la HCM Constanța

planck înmulțită cu viteza luminii

în vid înmulțită cu această diferență

între două inverse de numere cuantice

principale la pătrat mai exact

dacă tranziția Ce duce la emisie

fotonului are loc între nivelul

energetic și nivelul energetic

Enea feniciene Fie numele cuantice

principale corespund bineînțeles

energiilor a e și a f și Deci această

tranziție rezultă în emisie fotonului

cu energia H f atunci avem această

legătură dintre numărul de undă

și numerele cuantice principale

ale celor două energii celor două

nivele cu aceste două energii în

care bineînțeles n este mai mare

decât n f pentru a avea o emisie

dacă e n i ar fi mai mic decât

n f am avea o absorție de un anumit

Foton Deci întradevăr modelul bohr

reproduce legea seriilor spectrale

observat experimental coincidența

între lege experimentală și legea

teoretică sar întâmpla dacă numărul

sau Constanta riedberg care e măsurată

experimental arcul inchide cu acest

Factor Ce rezultă din modelul bohr

Deci dacă ar ar fi egal cu modul

din 1 împărțit la HC atunci am

avea o coincidență un o corespondență

perfectă între lege experimentală

și legea teoretică Și de ce am

putea conclude că seriile spectrale

ale atomului de hidrogen sunt foarte

bine descrisă de către modelul

bohr și întradevăr valoare experimentală

pentru r coincide sau are o valoare

foarte apropiată în ținând cont

de erorile experimentale de valoarea

lui R calculată cu ajutorul modulului

lui bohr prin această formulă modul

din 1 împărțit la HC împreună cu

energia de ionizare a atomului

de hidrogen despre care am discutat

în lecția trecută confirmarea Constantin

riedberg a validat modelul cuantic

al atomului propus de Bor Deci

mai exact după cum am discutat

în lecția trecută se poate măsura

energia de ionizare a atomului

de hidrogen și se poate verifica

dacă ea este egală cu predicția

modelului porcarie este modul din

Euro și întradevăr această coincidență

sau această corespondență dintre

valoarea măsurată experimental

și valoarea calculată Teoretic

are loc de asemeni după consultat

acum Constanța rydberg care se

poate măsura experimental și se

măsoară experimental este egală

cu modul din 1 împărțit la orice

Care este valoarea prezisă Teoretic

de modelul bohr Și de ce aceste

două rezultate au dus la confirmarea

modelului lui bohr Haideți să discutăm

acum despre liniile din seriile

spectrale observate experimental

Deci după cum am văzut modelul

lui bohr Propune o lege care este

în într o corespondență foarte

bună cu legea seriilor spectrale

și Deci numărul de undă este o

constantă Constanța rydberg înmulțită

cu această diferență de inverse

de pătrate de numere cuantice principale

numărul n f Stabilește seria spectrală

după cum am văzut iar în modelul

lui bohr n f este numărul cu Antique

principal al stării finale din

tranziție de asemeni este important

să observăm că o serie spectrală

va avea o limită adică un număr

de undă maxim care corespunde unei

valori ale lui n egal cu infinit

Pentru că dacă n este infinit Deci

tranziția are loc de pe un nivel

foarte înalt aflat Teoretic la

infinit atunci acest factor este

0 și atunci obținem valoarea maximă

a numărului de undă care va fi

Constanța rydberg împărțită la

numărul cuantic principal al stării

finale nf la pătrat gol Haideți

să vedem acum cum pot fi explicate

seriile aspect despre care am discutat

în prima lecție de fizică atomică

și anume liman ballmer passion

și așa mai departe Cum pot fi ele

explicate de către modelul bohr

Păi de ce trebuie să Considerăm

foarte simplu tranziții între nivelele

energetice ale atomului de hidrogen

De ce avem nivelul cu An egal cu

unu care este starea fundamentală

stare fundamentală și apoi nivelele

superioare avem un nivel n egal

cu 2 n egal cu 3 consider câteva

nivele pentru a putea reprezenta

apoi tranzițiile între ele n egal

cu patru uși haide să mai luăm

și un an egal cu 5 bineînțeles

ele continuă continuă în principiu

până la n egal cu infinit în funcție

de numărul de nivele pe care vrem

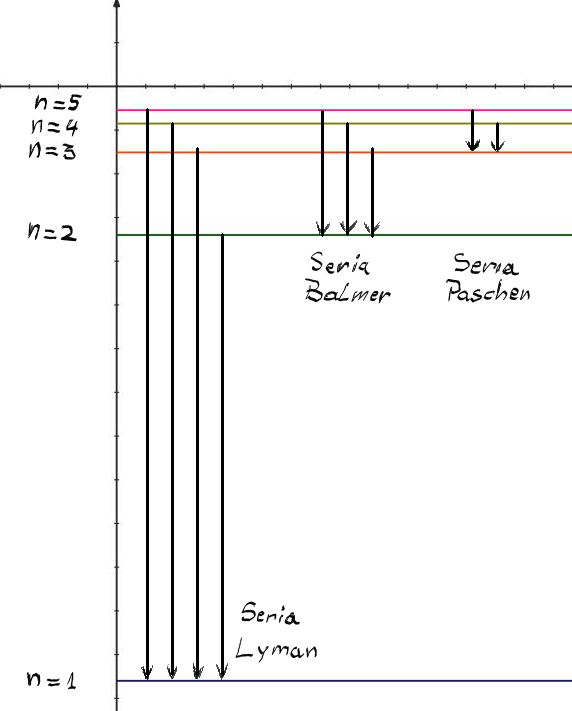
să le consideram după cum am văzut

prima serie spectrală corespunde

unui n f egal cu 1 Deci toate tranzițiile

ce au loc pe starea fundamentală

constituie o serie spectrală iar

această serie spectrală ce corespunde

lui n 1 egal cu 1 și m 2 egal cu

2 3 4 6 mai departe este binecunoscuta

serie leman Deci aceasta este seria

Liman ce apare în domeniul ultraviolet

Deci seria elimin din ultraviolet

care se observă experimental este

formată din toate tranzițiile de

pe stările excitate cu An egal

cu 2 3 4 5 așa mai departe dar

cu starea finală toate au starea

finală n egal cu unu adică starea

fundamental apoi avem seria ballmer

următoarea serie sta ballmer Care

este formată din toate tranzițiile

care au starea finală n egal cu

doi Deci aceste tranziții care

au în unu egal cu doi de numărul

cuantic principal ce corespunde

numărului seriei va fi in 1 egal

cu 2 iar n i sau an doi va fi vor

fi egal cu 3 4 5 și așa mai departe

această Toate aceste tranziții

formează așa numita serie ballmer

seria ballmer care după cum am

văzut experimental are loc în spectrul

vizibil și așa mai departe următoarea

serie passion va avea loc sau va

fi formată din toate tranzițiile

care au ca stare finală starea

in 1 egal cu 3 ești toate tranzițiile

care au loc cu finalitatea tranziții

pe an 1 egal cu 3 vor Formați seria

pași și așa mai departe Deci vedem

întradevăr Cum poate fi explicat

foarte elegant toată pot fi explicate

foarte elegant toate rezultatele

seriilor spectrale ale atomului

de hidrogen dacă vreți putem reprezenta

vizual și altfel aceste tranziții

De ce avem atomul de hidrogen care

are un nucleu În centru nucleul

cu sarcina plus unu și în jurul

lui bineînțeles avem orbitalii

electronici care corespund nivelelor

energetice Deci Să considerăm câteva

foarte schematic De ce am avem

în acest desen nivele energetice

pentru n egal cu 1 an egal cu 2n

egal cu 3 și egal cu 4 atunci seria

ballmer va fi formată din toate

tranzițiile electronilor de pe

nivelele superioare pe nivelul

pe starea fundamentală n egal cu

Deci seria ballmer va fi formată

din aceste tranziții Deci aceasta

este seria balm seria liman va

fi formată din toate tranzițiile

cu starea finală pe prima stare

excitată adică cea cu An egal cu

2 din seria ballmer va fi formată

din tranziții de felul acesta nu

avem numai două în schema noastră

Bineînțeles dacă am fi folosit

și alte nivele energetice cu n

mai mare decât 4 egal cu 5 și mai

departe am fi avut și alte tranziții

în seria seria balmez scuzați prima

serie am făcut o greșeală aici

prima serie este bine înțeles liman

și cea de a doua serie este ballmer

lehman este seria cu starea finală

a n egal cu 1 ballmer este seria

cu starea finală n egal cu 2