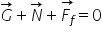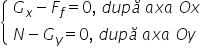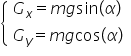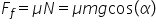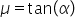Legile forţei de frecare. Rezolvarea problemei corpului pe un plan înclinat.
Tag-uri
Partajeaza in Google Classroom

Transcript
în cea de a obții de mecanică Donia
nu vom discuta despre forța de
frecare și despre mișcarea unui
corp pe un plan înclinat frecare
am apare la suprafața de contact
a două corpuri solide și are ca
principală cauză asperitățile de
pe cele două suprafețe aflate în
contact dar și atracția de tip
molecular sau electrostatic ce
apare la cele două suprafețe în
contact pentru a exemplifica să
avem să luăm în considerare Un
corp care are o suprafață cu asperități
care se află în contact cu suprafața
altui corp care are și el bineînțeles
asperități acest asperități se
întrepătrund și bineînțeles că
dacă Încercăm să mișcăm unul din
corpuri față de celălalt ele se
vor opune de mișcări vor dezvolta
o forță de rezistență Deci frecare
am este apariția unor forțe de
rezistente de rezistență numită
forțe de frecare ce se opune mișcării
sau începerii mișcări există trei
tipuri de frecare și anume statică
care se opune punerii în mișcare
a unui corp aflat în repaus avem
și eu o frecare la alunecare care
se opune mișcării prin alunecarea
unui corp și o frecare la rostogolire
care se opune mișcării prin rostogolire
a unui corp principalul tip în
toate situațiile practice de frecare
este frecare la alunecare Deci
dacă nu specificăm Ce fel de frecare
despre ce fel de frecare Vorbim
ne referim la plecarea de la alunecare
Pentru a măsura forțele de frecare
folosim un dispozitiv experimental
simplu avem o suprafață pe care
punem un corp care este atașat
cu un fir de Un scripete și la
capătul scripetelui avem un taler
pe care punem diferite greutăți
cunoscute pentru a măsura forța
de frecare statică pur și simplu
creștem greutatea de pe taler până
când corpul se pune în mișcare
valoarea greutății pentru care
corpul se pune în mișcare este
egală cu forța de frecare statică
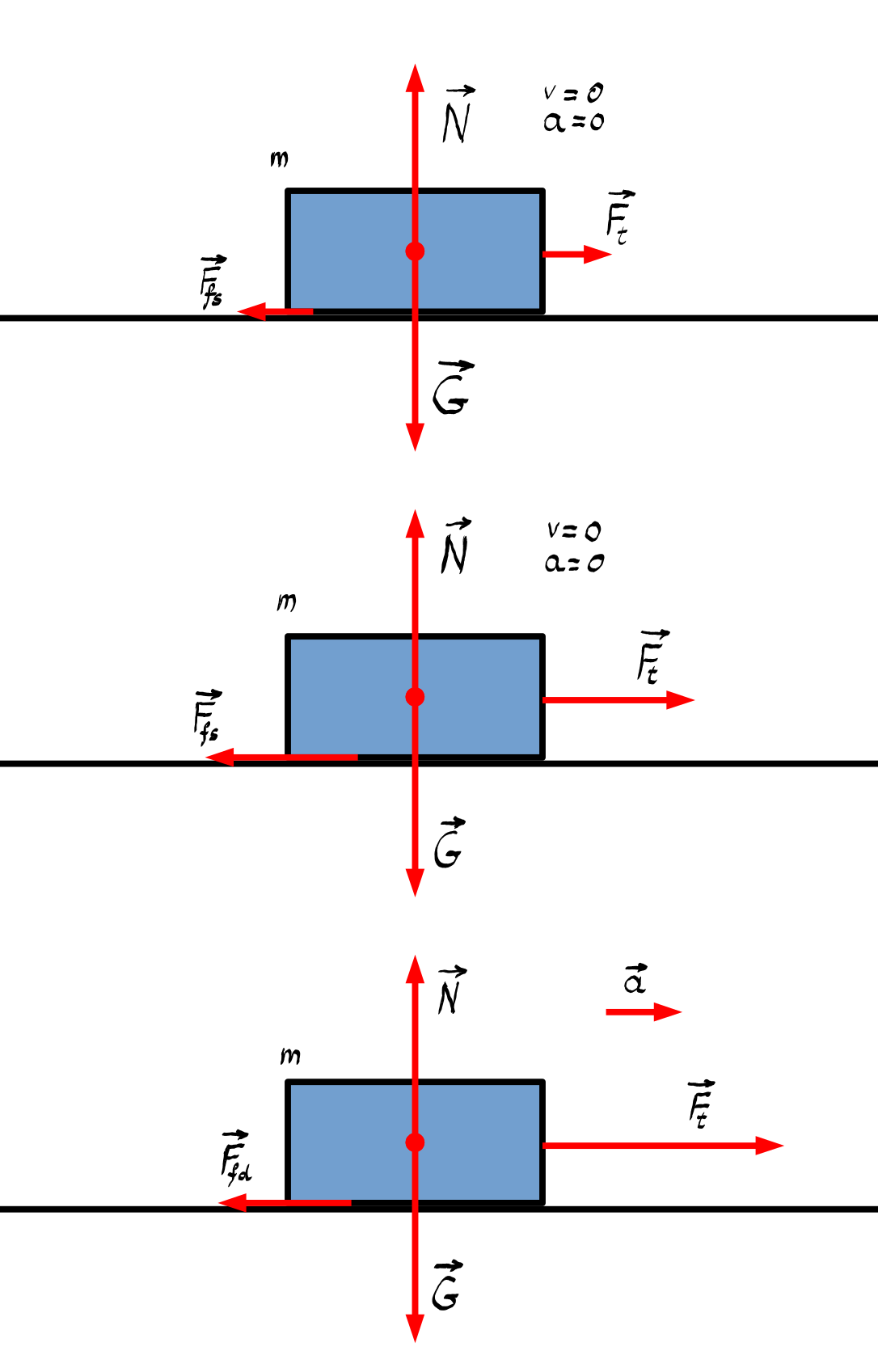
forța de frecare apare la suprafața
de contact și are sens opus mișcării
forța de Pentru a măsura forța
de frecare la alunecare o dată
ce corpul se află în mișcare very
m greutățile de pe taler până când
corpul are o mișcare uniform asta
înseamnă că accelerația lui este
0 dacă accelerația lui este 0 conform
principiului al doilea al mecanicii
forța rezultantă ce acționează
asupra corpului este 0 deci a egal
cu 0 implică că Forța de tracțiune
care este și tensiunea din fir
este egală cu forța de frecare
dar Forța de tracțiune este egală
cu greutatea de pe taler Deci aceasta
este forța de tensiune din fir
și aceasta este greutatea și de
tei este egal cu g în concluzie
în acest caz forța de frecare este
dată de greutatea de pe talere
și în felul acesta putem măsura
forța de frecare la alunecare pentru
a măsurat forța de frecare la rostogolire
schimbăm un pic dispozitivul experimental
în sensul că punem între corp și
suprafață câțiva cilindri și în
acest caz corpul se va mișca prin
rostogolirea acestor cilindri și
respect repetăm același experiment
și măsurăm în felul acesta a forța
de frecare la rostogolire primă
concluzie pe care o trage din nas
fel de măsurători este că pentru
același corp pe aceeași suprafață
forța de frecare statică este întotdeauna
mai mare decât forța de frecare
are la alunecare care la rândul
ei este întotdeauna mai mare decât
forța de frecare la rostogolire
vom continua acest tip de măsurători
pentru a vedea De ce depinde sau
care sunt parametrii de care depinde
forța de frecare la alunecare care
din nou este principalul tip de
forță de frecare Deci Variant parametri
corpului și a suprafeței și obținem
că forța de frecare la alunecare
nu depinde de aria de contact putem
varia dimensiunile corpului și
putem observa că forța de frecare
Nu depind nu depinde de aceste
dimensiuni ea în schimb depinde
de natura sau de gradul de prelucrare
a suprafeței de contract contact
de simplu facem experimentul pentru
un corp de lemn de exemplu și o
de lemn și apoi pentru un corp
de oțel pe o suprafață de lemn
și observăm că magnitudinea forței
de frecare depinde de natura materialelor
din care sunt făcute atât corpul
cât și suprafața ia depinde de
asemeni și de gradul de prelucrare
pentru aceleași două combinații
corpul suprafață să zicem lemn
lemn Dacă aceste două suprafețe
de lemn se mai bine prelucrate
atunci forța de frecare este mai
mic și în final ia depinde direct
proporțional de forța normală a
suprafețelor amintesc prin forță
normală a unei suprafețe pe care
se află un corp înțelegem forța
de reacțiune a suprafeței la greutatea
corpului Deci greutatea corpului
acționează asupra suprafeței cu
o forță g și în concluzie conform
principiului 3 al mecanicii suprafața
va reacționa cu o forță numită
forța normală în acest tip de dispozitiv
forța normală este egală cu forța
de greutate dar dacă suprafața
este Înclinată face un unghi cu
orizontala atunci forța normală
nu va mai fi egală cu greutatea
pentru că ele își forța normală
este aceeași aceasta e greutate
este aceasta ele nu mai sunt egale
nemaiavând aceeași direcție revenind
se observă experimental că forța
de frecare este direct proporțională
cu această forță normală de reacție
a suprafeței la greutatea corpului
în concluzie el se trage conclusivă
că forța de frecare este egală
cu un o constantă numit coeficient
de frecare înmulțită cu această
forță normală a suprafeței coeficientul
de frecare la alunecare ia o valoare
fixă pentru un corp și o suprafață
dat vedeți aicea un tabel cu diferite
suprafețe tipuri de suprafețe și
corpuri și valorile pentru coeficientul
de frecare la alunecare miu și
cu F centrul de frecare static
mus observăm că întotdeauna mai
este mai mare decât mine Deci frecarea
statică este mai puternică decât
cealaltă care și că el Ia o valoare
dată pentru o ție corp suprafață
fiind o forță rezistentă consecințele
forței de frecare sunt de obicei
nedorite în toate aplicațiile tehnologice
și în consecință sau dezvoltat
tot felul de tehnologii pentru
a reduce efectul unul una din aceste
tehnologii este descreșterea coeficientului
de frecare prin lubrifierea mecanismelor
în această imagine vedem un motor
care arde de combustibil pentru
a genera mișcarea oscilatorie a
pistoanelor Care este transmisă
mai departe prin mecanismul de
transmisie a mișcării din mașina
respectivă dacă nu am găsit nicio
soluție pentru frecarea dintre
toate aceste componente la motorul
sar încălzi și în final se defecta
acesta este motivul pentru care
toate mecanismele din varii mașini
folosesc uleiuri pentru lubrifierea
componentelor aflate în mișcare
și contact Deci care generează
frecare o altă tehnologie este
transformarea frecării la alunecare
între frecare la rostogolire aceasta
este folosită de obicei în rulmenți
Spre exemplu prin plasarea unor
bile ce se rostogolesc între cele
două suprafețe aflate în mișcare
și în contact Nu toate consecințele
frecării sunt în negative cel mai
simplu exemplu fiind mișcarea noastră
mersul nu am putea merge dacă încălțămintea
noastră nu ar dezvolta o forță
de frecare cu suprafața pe care
ne deplasăm același lucru este
valabil și pentru automobile pentru
a discuta un pic despre forța de
frecare la rostogolire dintre roțile
unui automobil și suprafața pe
care automobilul se deplasează
să desenăm Un automobil aceasta
este schema unui automobil care
se mișcă în această direcție de
ce aceasta este vectorul viteză
Dacă primul set de roți cel din
față este setul de roți motoare
necesitatea sunt roțile motoare
iar iar roțile din spate sunt roțile
inert aceasta înseamnă că roțile
din față sunt cuplate la motor
pe când cele din spate Nu sunt
cuplate să ne cuplate la motor
atunci forțele de frecare la rostogolire
vor fi foarte diferite în sensul
lor mai exact roțile motoare au
frecare la rostogolire ce dezvoltă
o tracțiune o forță de tracțiune
sensul forțelor de frecare rostogolire
a roților motoare fiind înainte
pe când roțile inert a a o forță
de frecare la rostogolire ce are
sens opus mișcării automobilului
Și de ce le vor fi în forță de
frânare de ce trebuie să ținem
cont întotdeauna la un automobil
când desenăm sensul când stabilim
sensul forțelor de frecare la rostogolire
de faptul Dacă roțile sunt motoare
sau sunt inert Adică dacă sunt
cuplate la motor sau ne cuplate
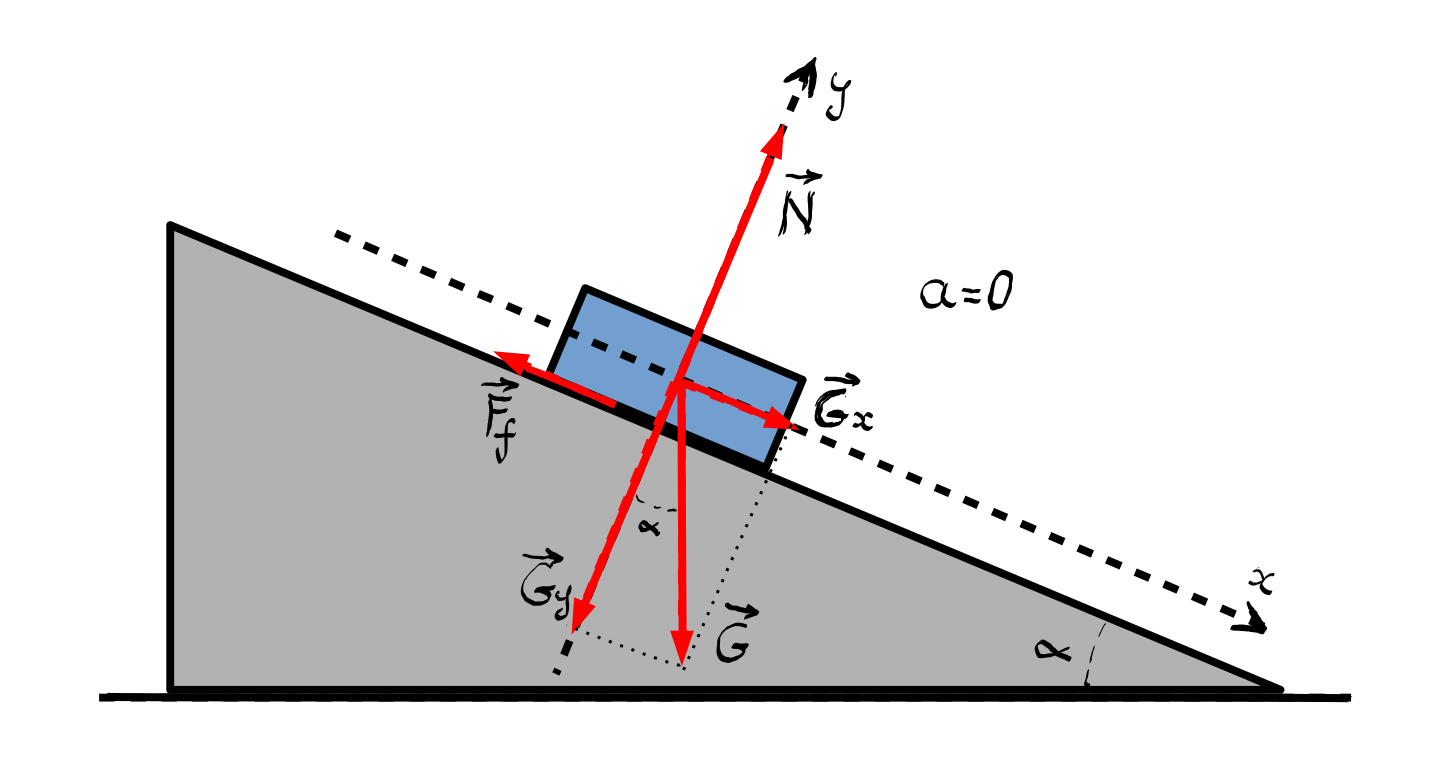
la motor în fine Să considerăm
problema unui corp aflat pe un
plan înclinat 10 avem un corp de
masă M ce se află pe un plan înclinat
cu unghiul Alfa Care este tras
de o forță f care face un unghi
Baton cu planul înclinat și dorim
să calculăm accelerația corpului
începem prin a desena forțele ce
acționează asupra corpului bineînțeles
vom avea o forță de greutate care
are sensul verticalei în punctul
respectiv vom avea o forță normală
Care este reacțiunea suprafeței
la acțiunea greutății corpului
și vom avea și o forță de frecare
care acționează dea lungul suprafeței
după ce am stabilit toate forțele
ce acționează asupra corpului putem
scrie ecuația fundamentală a dinamicii
și anume că suma forțelor suma
vectoriala for Florin f plus n
plus G Plus forța de frecare f
f este egală cu masa înmulțită
cu accelerația corpului pentru
a rezolva această ecuație alegem
un sistem de axe de coordonate
o x o y în care o x este de a lungul
planului iar o este perpendiculară
pe planul înclinat și atunci putem
scrie de a lungul lui o x că e
f cosinus de beton plus sinus de
Alfa minus ff forța de frecare
este egală cu masa ori accelerația
masa ori accelerația pentru corpul
se mișcă numai în direcția x iar
componentele sunt imediate de fix
este această componentă și va fi
f cosinus de Betta iar gx este
această componentă și deoarece
acest unghi este egal cu unghiul
planului Alfa gx va fi gen înregistrez
Alfa pe o y a m f sinus de beton
plus G scuzați minus G cosinus
Delfin plus n este egal cu zero
zero pentru că nu avem accelerație
pe direcția oi corpului se mișcă
pe o y și componentele sunt f y
este acesta de ce este f sinus
de beton iar G Y este acesta Deci
G cosinus de Alfa și are semnul
minus pentru că jy8 A are Sensul
opus a XA o y în cea de a doua
ecuații scrie în rezultă valoarea
sau ecuația pentru forța normală
n este egal cu g cosinus de Alfa
Dică mg cosinus de Alfa minus f
sinus de beton iar din prima ecuație
avem m a este egal cu EF cosinus
de beton plus mg sinus de Alfa
minus m n forța de frecare este
produsul dintre coeficientul de
frecare la alunecare și forța normală
de aici putem scoate ecuația pentru
accelerația A care devine egală
cu g pe lângă țin Alpha minus Mucosolvan
plus f împărțit la m pe lângă cosinus
de Betta plus musings de Betta
și aceasta este ecuația pentru
accelerația corpului Pe planul
înclinat

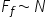
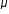 .
.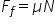
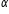 .
.