Lentile divergente - caracteristici, formarea imaginilor. Formula convergenţei lentilelor.

în cea de a patra lecții de optică

geometrică vom discuta despre lentila

divergenta și despre convergența

lentilelor lentila divergenta este

o lentilă concavă subțire în lecția

precedentă cu numărul 3 am discutat

despre clasificarea lentilelor

în funcție de geometria suprafețelor

lor și o lentilă concavă avea următoarea

formă lentile divergente sunt prezentate

schematizat ca o ca un segment

de dreaptă cu două săgeți răsturnate

la capăt ca în această schemă tot

în lecția precedentă am introdus

noțiunile de axa optică principală

și axa optice secundare ale unei

dentină un fascicul cilindric paralel

cu Axa optică principală precum

cel desenat cu culoarea albastră

în această schemă va merge după

refracție din lentila ca și cum

ar fi pornit din focarul principal

imagine exprima după cum se vede

în această schemă de asemeni un

fascicul cilindric paralel cu Axa

optică secundară precum cel prezentat

cu verde în această schemă va merge

după refracție din ala ca și cum

ar fi pornit din focarul secundar

imagine F1 prin colecția tuturor

focarelor secundare imagine de

tipul F 1 prim formează planul

focal imaginea care este perpendicular

pe axa optică principală și se

află la o distanță de lentilă notată

cu F prim care se numește distanță

focală imagine și prin convenție

este considerată negativă ceea

ce este invers decât pentru lentile

convergente a unde distanța focală

imagine era pozitivă un fascicul

convergent din focarul principal

obiect devine paralel cu Axa optică

principală deci în această schemă

avem un fascicul convergent către

focarul principalul obiect iar

după refracție el va deveni paralel

cu Axa optică principală de asemeni

un fascicul convergent în un focar

secundar obiecte F1 va merge după

refracție din lentilă paralel cu

ac axa optică secundară colecția

tuturor focarelor secundare obiecte

tipul F 1 formează planuri focal

obiect linia roșie întreruptă în

desenul nostru care se află la

o distanță f de lentilă numită

distanța focală obiect care este

luată prin convenție ca fiind pozitivă

din nou lentilă convergentă are

semnele opuse Deci distanța focală

obiect a lentilei convergente este

negativă continuăm cu formarea

imaginilor în lentile divergente

ca și în lecția precedentă când

am discutat despre formarea imaginilor

în lentile convergentă folosim

același set de trei raze și anume

cu albastru raza incidența paralelă

cu Axa optică principală și reflectată

prin focarul principalii medgyn

exprim cu roșu rod raza incidență

prin focarul principal obiect reflectată

paralel cu Axa optică principală

și cu verde raza incidență prin

centrul Optic al lentilei Care

este reflectată fără de viață în

primul caz studiat în obiectul

notat cu a b se află la o distanță

de lentilă mai mare decât dublul

distanței focale punctul H prim

Este un punct aflat la dublul distantei

focale deci de este mai mare decât

doi mergi prin distanța focală

și trasăm cele trei rase cu albastru

raza incidență paralel cu Axa optică

principală care este reflectată

ca și cum ar veni din focarul principal

imagine cu roșu raza incidență

în Prelungirea a prind focarul

principal obiect care este reflectată

paralel cu Axa optică principală

și cu verde raza incidență prin

centrul Optic al lentilei reflectată

fără deviație în mod Evident fasciculul

reflectat este divergente Deci

razele refractate se întâlnesc

doar în prelungirile lor și imaginea

a prim b prim are următoarele proprietăți

este virtuală adică se formează

la prelungirile razelor este dreaptă

Adică are aceeași orientare ca

obiectul și este mai mic următorul

caz studiat este cel în care obiectul

se află între între în focarul

principal imagine și dublul distanței

focale Deci 2f prim mai mare decât

n mai mare decât primul cele trei

raze sunt următoarele cu albastru

raza paralelă cu Axa optică principală

care este reflectată ca și cum

ar veni din focarul principal imagine

cu roșu raza incidență prin focarul

principal obiect în Prelungirea

a Care este reflectată paralel

cu Axa optică principală și cu

verde raza incidență prin centrul

Optic al lentilei reflectată fără

deviații la fel fasciculul reflectat

este divergente de ce razele se

vor întâlni în prelungirile lor

vom avea din nou o imagine virtual

Deci proprietățile imagini sunt

virtuală drepte aceeași orientare

cu obiectul adică și mai mică ultimul

caz analizat este cel în care obiectul

este virtual și se află de partea

cealaltă a lentilei adică între

centrul Optic și focarul principal

obiect Deci cazul obiect virtual

de mai mic decât Scrie un comentariu

obiect virtual înseamnă că obiectul

în sine este o imagine formată

de către un alt instrument optic

lasa în cele trei raze Deci cu

albastru raza incidentă paralelă

cu Axa optică principală și apoi

reflectată ca și cum ar veni din

f prim notezi din nou că deoarece

obiectul este virtual el Trebuie

să se formeze la intersecția razelor

incidente obiectul se va forma

la intersecția razelor incidente

iar imaginea la intersecția razelor

refractate următoarea rază cu roșu

incidentă prin focarul principal

obiect și reflectată paralel cu

Axa optică principală obiectul

se află la prelungirea razei incidente

și cea de a treia incidentă prin

centrul Optic al lentilei și refractata

fără de viață la intersecția celor

trei raze refractate se va afla

imaginea cele trei raze reflectate

se întâlnesc Deci imaginea va fi

rea în concluzie proprietățile

imagini în acest caz sunt este

reală este dreaptă Adică are aceeași

orientare cu obiectul și este mai

mare convergența unei lentile se

notează cu ce se măsoară în dioptrii

și este definită ca inversul distanței

focale exprimată în metri această

mărime se introduce deoarece capacitatea

unei lentile convergente a de a

converge razele este invers proporțională

cu distanța focală la fel capacitatea

unei lentile divergente de adevăratele

invers proporțională cu distanța

focală convergență se măsoară în

dioptrii dioptria se notează cu

litera grecească Delta si aceasta

e simbolul pentru dioptrie și convergența

are semn pozitiv pentru lentile

convergente a și semnul negativ

pentru lentile divergente o dioptrie

se definește ca convergența unei

lentile cu distanța focală de un

metru formula care Stabilește relația

dintre convergența unei lentile

și razele celor două suprafețe

ale lentilei este următoarea ce

egal cu n minus 1 indicele de refracție

minus 1 înmulțit cu diferența dintre

inversul razelor 1 pe 1 minus 1

pe 2 unde era nu este raza suprafeței

prin care pătrunde lumina și F2

este raza suprafeței prin care

iese lumină pentru o lentilă convergentă

schema arși următoare Deci ce 2

este centrul cele de două suprafețe

și c 1 este centrul primei suprafețe

mici acesta este aerul 1 acesta

este doi și raza incidența vine

din dinspre direcția centrului

C2 și apoi este refractat
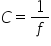
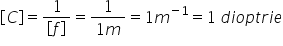
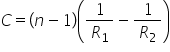
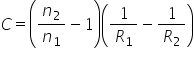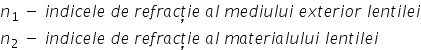