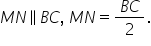Linia mijlocie în triunghi (aplicații)

ne propunem să rezolvăm două probleme

în care vom aplica proprietățile

liniei mijlocii a unui triunghi

prima problemă triunghiul abc este

echilateral iar m n și p sunt mijloacele

laturilor ab bc și ac știind că

ab este egal cu 10 cm Aflați perimetrul

triunghiului MNP dacă a b c este

un triunghi echilateral înseamnă

că acesta are toate laturile congruente

Așadar vom scrie că ab este egal

cu bc egal cu AC și egal cu 10

cm pentru a afla perimetrul triunghiului

MNP trebuie să aflăm lungimea segmentelor

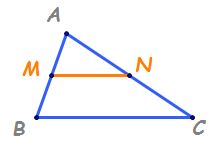
MN NP și mp Dacă punctul M este

mijlocul laturii ab și punctul

n este mijlocul laturii BC ma rezultat

că se numesc tul m n este linie

mijlocie în triunghiul abc m n

este paralelă cu AC și nu avea

lungimea egală cu jumătate din

lungimea laturii AC rezultă MN

egal cu AC supra 2 AC este 10 cm

MN are lungimea egală cu 5 cm Dacă

n este mijlocul lui BC și P este

mijlocul laturii ac înseamnă că

segmentul NP este linie mijlocie

iar NP va fi paralelă cu AB și

egal cu jumătate din AB egal cu

10 supra 2 și Gal cu 5 cm mp este

linie mijlocie în triunghi rezultă

mp va fi egală cu jumătate din

lungimea laturii BC și gală cu

5 cm observăm Așadar că și triunghiul

MNP este un triunghi echilateral

și acum ca să aflăm perimetrul

acestui triunghi vom însuma lungimile

laturilor perimetrul triunghiului

MNP a fi egal cu m n plus m p plus

m p egal cu 3 ori 5 egal cu 15

cm și a doua problemă în patrulaterul

a b c d punctele m n p și q sunt

mijloacele laturilor ab bc cd și

AD la punctul A trebuie să arătăm

că patrulaterul m n p q este paralelogram

și la punctul b dacă r și s sunt

mijloacele diagonalelor Arătați

că n r q s este paralelogram începem

cu punctul a pentru a demonstra

că mnpq este paralelogram vom arăta

că acesta are două laturi opuse

paralele și congruente de exemplu

p n și q m n duce diagonala DB

și observăm că sa format astfel

două triunghiuri Triunghiul cdb

și triunghiul adb dacă pești și

n sunt mijloacele laturilor BC

și bc înseamnă că pe n este linie

mijlocie în triunghiul cdb deci

pe an va fi paralelă cu d b și

va avea lungimea egală cu jumătate

din lungimea laturii de b apoi

este ne mutăm în celălalt triunghi

a d b punctele q și m sunt mijloacele

laturilor ad și ab înseamnă că

segmentul qm este linie mijlocie

in acest triunghi Deci q&a va fi

paralelă cu d b și jumătate din

DB va rezulta Așadar că segmentele

MN și PN sunt congruente deoarece

fiecare dintre acestea are lungimea

egală cu jumătate din lungimea

segmentului DB și ele vor fi și

paralele pentru că Ambele sunt

paralele cu DB am arătat Așadar

că patrulaterul m n p q are două

laturi opuse paralele și congruente

de fier va fi paralelogram dacă

pe este mijlocul laturii DC și

n este mijlocul laturii CB A rezultat

că pe an este linie mijlocie în

triunghiul cdb rezultă pe an este

paralelă cu d b și pe an este jumătate

din lungimea laturii DB nu te această

relație cu cu unu apoi în triunghiul

adb punctul q este mijlocul segmentului

ad punctul M e este mijlocul laturii

ab rezultă segmentul qm este linie

mijlocie în triunghiul adb rezultat

um va fi paralelă cu d d și jumătate

din lungimea laturii DB și notez

această relație cu doi din relațiile

1 și 2 rezultă că aceste două laturi

q m și p n sunt paralele pe n este

paralelă cu q m și ele vor fi și

congruente pentru că amândouă au

lungimea egală cu jumătate din

lungimea laturii DB deci pe n este

egal cu q m va rezulta din această

relație că patrulaterul m n p q

este paralelogram am terminat punctul

A continuăm cu punctul b bancnota

cu r și s mijloacele diagonalelor

patrulaterului a b c d mai întâi

ducem și diagonala AC notam cu

M mijlocul diagonalei AC și cu

s mijlocul diagonalei DB trebuie

să arătăm că patrulaterul n r q

s este paralelogram fie R mijlocul

diagonalei ac she is mijlocul diagonalei

de b nu folosi același raționament

ca și la punctul a și vom arăta

că acesta are două laturi opuse

paralele și congruente de exemplu

r n și q s Dacă n este mijlocul

laturii ac și n este mijlocul laturii

bc înseamnă că r n este linie mijlocie

în triunghiul c a b chiar an va

fi paralelă cu AB și jumătate din

AB acum să ne uităm În triunghiul

d a b punctul q este mijlocul laturii

a d și punctul s este mijlocul

laturii BD înseamnă că segmentul

e f este linie mijlocie în triunghiul

DAB Deci QS va fi paralelă cu AB

și jumătate din AB din moment ce

este eggman tele r n și q s au

lungimea egală cu jumătate din

lungimea segmentului AB înseamnă

că ele vor fi congruente și de

asemenea aceste laturi vor fi și

paralele pentru că ele sunt paralele

cu AB segmentul rn este linie mijlocie

în triunghiul c ab rn este paralelă

cu AB și r n este jumătate din

AB botez acestei relații cu trei

apoi q s este linie mijlocie în

triunghiul DE ab rezultat QS va

fi paralelă cu AB și QS va fi jumătate

din AB și notez acestei relații

cu 4 din relațiile 3 și 4 va rezulta

că rn este paralelă cu latura QS

și cele două segmente au aceeași

lungime n egal cu q s rezultă că

Patrulaterul mnpq este paralelogram

am demonstrat și punctul b