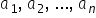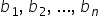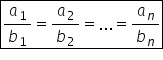Mărimi direct proporţionale

în această lecție o să vedem ce

sunt mărimile direct proporționale

Să presupunem că avem un creion

care costă 2 RON atunci două creioane

vor costa 4 RON iar trei creioane

vor costa 6 RON observăm că dacă

numărul de creioane crește atunci

crește și prețul acestora mai exact

dacă numărul de creioane se dublează

atunci și prețul acestora se dublează

iar dacă numărul de creioane se

Triplează atunci și prețul acestora

va crește de trei ori în acest

caz spune că aceste mărimi sunt

mărimi direct proporționale două

mărimi sunt direct proporționale

Dacă depind una de alta astfel

încât dacă una crește de n ori

Atunci și cealaltă crește tot de

n ori cu aceste mărimi Putem să

scriem niște rapoarte am văzut

că un creion costă 2 RON așa dar

putem să scriem raportul 1 supra

2 două creioane costă 4 ron Deci

avem raportul 2 supra 4 iar trei

creioane costă 6 RON cu aceste

rapoarte putem să formăm niște

proporții pentru că 1 supra 2 este

egal cu 2 supra 4 sau o altă proporție

doi supra 4 egal cu 3 supra 6 și

acum să dăm în continuare definiția

pentru mărimile direct proporționale

numerele x și y sunt direct proporționale

cu numerele a și b dacă x supra

a este egal cu y supra b în general

numerele a1 a2 a3 puncte puncte

a n sunt direct proporționale cu

numerele B1 B2 bn dacă formează

șirul de rapoarte egale a 1 supra

b 1 egal cu a 2 supra b-2 egal

cu puncte puncte a n supra b n

să facem o continuare o problemă

Să se afle numerele x și y știind

că sunt direct proporționale cu

numerele 5 și 8 și că 2x minus

y este egal cu 40 această relație

de proporționalitate se mai poate

înota și astfel numerele x și y

sunt direct proporționale cu numerele

5 și 8 înseamnă că are loc următoarea

proporție x supra 5 este egal cu

y supra 8 fiind dat această proporție

trebuie să aflăm numerele x și

y mai știm și că 2x minus y este

egal cu 40 ca să putem folosi și

această relație dată în problema

Trebuie să amplificăm primul raport

cu doi astfel încât să ne apară

2x Așadar amplificăm primul raport

cu 2 și obținem următoarea proporție

2 supra 10 egal cu y supra 8 în

lecția în care am învățat proporțiile

am văzut că putem să obținem proporții

derivate dacă scădem numărătorii

între ei și numitorii între ei

Așadar aceste rapoarte Se pot lega

la în continuare cu raportul format

de diferența numărătorilor și diferența

numitorilor dar 2x minus y este

egal cu 40 ia 10 minus 8 este egal

cu 240 supra 2 este egal cu 20

și acum ca să aflăm numerele x

și y egalăm aceste rapoarte cu

20 prin urmare 2 x supra 10 va

fi egal cu 20 de unde rezultă că

2x este egal cu 10 ori 20 adică

2 x este egal cu 200 și împărțind

la 2 în Ami membrii obținem că

x este egal cu 100 află pe y din

Galați spre port cu 20 y supra

8 este egal cu 20 rezultă că y

este egal cu 8 ore 20 euro sută

și y egal cu 160 și mai facem o

problemă dacă din 120 kg de sfeclă

se obțin 40 kg de zahăr din câte

kilograme de sfeclă se vor obține

60 kg de zahăr acest gen de probleme

se rezolvă cu regula de trei simple

Așadar să scriem regula de trei

simpla astfel dacă din 120 kilograme

de sfeclă se obțin 40 kg de zahăr

din câte kilograme de sfeclă adică

x kilograme de sfeclă se vor obține

60 kg de zahăr numărul de kilograme

de sfeclă și numărul de kilograme

de zahăr sunt mărimi direct proporționale

Pentru că atunci când numărul de

kilograme de sfeclă va crește Cu

siguranță va crește și numărul

de kilograme de zahăr și atunci

proporția se scrie în felul următor

120 supra x este egal cu 40 supra

60 trebuie să aflăm necunoscuta

x din această proporție x va fi

egal cu 120 ori 60 supra 40 si

simplifică 120 cu 40 120 împărțit

la 40 este 3 Așadar x este egal

cu trei ori 60 180 kg de sfeclă