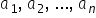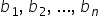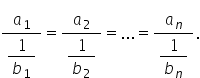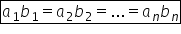Mărimi invers proporţionale

circulând cu 50 de km la oră o

mașină parcurge o distanță în 4

ore În cât timp ar parcurge distanța

dacă ar circula cu 100 de km la

oră circulând cu 50 de km la oră

o mașină parcurge distanța în 4

ore Dacă ar circula cu 100 de km

la oră atunci timpul necesar parcurgerii

distanței va fi mai mic mai exact

O să fie de două ore observăm că

dacă viteza crește timpul o să

scadă Dacă viteza se dublează timpul

se va micșora de două ori nu spune

Așadar că cele două mărimi adică

viteza și timpul sunt mărimi invers

proporționale observăm că 50 ori

patru este egal cu 100 ori 2 deoarece

200 este egal cu 200 această relație

va duce la următoarea proporție

50 supra 1 supra 4 egal 100 supra

1 supra 2 putem să scrie ma ceastă

relație sub forma acestora fracții

supraetajate și tu să vedem ce

înțelegem mai exact prin numere

invers proporționale sau mărimi

invers proporționale două mărimi

sunt invers proporționale Dacă

d fiind una de alta a astfel încât

dacă una crește de n ori cealaltă

se micșorează de n ori numerele

x și y sunt invers proporționale

cu numerele a și b dacă sunt direct

proporționale cu inversele lor

adică x supra 1 pe a egal cu y

supra 1tb sau putem scrie a x egal

cu b y în general numerele a1 a2

puncte puncte a n sunt invers proporționale

cu numerele B1 B2 bn dacă formează

șirul de rapoarte egale a 1 supra

1 pe B1 egal cu a 2 supra 1 pe

2 egal cu a ad supra 1 pe b n Determinați

numerele a b și c știind că sunt

invers proporționale cu numerele

2 3 și 5 și că a plus b plus c

este egal cu 62 Dacă a b și c sunt

invers proporționale cu doi trei

și cinci puteri scrie Acest lucru

astfel 2 a egal cu 3 b egal cu

5c sau Putem să scriem că a supra

1 pe 2 este egal cu b supra 1 pe

3 egal cu c supra 1 pe 5 dar ca

să nu lucrăm cu fracții supraetajate

prefer să folosim prima relație

scrisă această relație se poate

egala în continuare cu un număr

oarecare și atunci 2-a este egal

cu k și împărțind la 2 membru cu

membru obținem că a este egal cu

k supra 2 dacă 3 b este egal cu

k împărțind la 3:00 membru cu membru

obținem că b este egal cu k supra

3 iar dacă 5 c este egal cu k putem

împărțit la 5 și obține că ce este

egal cu k supra 5 Acum ne folosim

de această relație dat în problemă

și anume a plus b plus c egal cu

62 a plus b plus c va fi egal cu

62 în loc de a scrie k supra 2

în loc de bebe scrie că apa supra

3 și în loc de ce cum scrie k supra

5 Deci k pe 2 plus kp3 plus apa

pe 5 este egal cu 62 ca să adunăm

aceste trei fracții trebuie să

le aducem la numitor comun numitorul

comun este 2 ori 3 ori 5 adică

30 prima fracție sale amplifica

cu 15 a doua fracție cu 10 și a

treia fracție cu 6 rezultat continuare

că 15k supra 30 plus 10 k supra

30 plus 6k supra 30 este egal cu

62 15 plus 10 și plus 6 este 31k

supra 30 egal cu 62 de unde rezultă

că 31k este egal cu 30 ori 62 împărțim

relația la 31 și obținem apa egal

cu 30 ori 62 supra 31 Nu am vrut

să efectuez această înmulțire deoarece

am observat că 62 este un multiplu

al lui 31 deci putem să simplificăm

cu 3162 împărțit la 31 este 23148

este 1 Deci că apa va fi egal cu

30 ori 2 Adică că apa va fi egal

cu 60 acum pe la aflat pe k va

fi foarte ușor să aflăm numerele

a b și c a este egal cu k supra

2 adică cu 60 supra 2 care este

egal cu 30 b va fi egal cu k supra

3 adică 60 supra 3 care este egal

cu 20 și ceva Fie a egal cu k supra

5 mai exact 60 supra 5 care este

egal cu 12 am aflat cele trei numere

1 zi ma problemă Dacă 12 muncitori

termina o lucrare în 10 zile sunt

câte zile ar termina lucrarea 15

muncitori Nu scrie din nou regula

de trei simpla pentru această problemă

12 muncitori termină o lucrare

în 10 zile 15 muncitori ar termina

lucrarea în x zile să vedem întâi

Dacă aceste mărimi sunt direct

sau invers proporționale dacă numărul

de muncitori va crește atunci numărul

de zile o să scadă deoarece prin

mai mulți muncitori lucrarea se

va termina mai repede în acest

caz mărimile sunt invers proporționale

și atunci regula de trei simpla

pentru mărimi invers proporționale

se va scrie astfel 12 supra 15

egal cu x supra 10 atenție Deci

când mărimile sunt invers proporționale

al doilea raport se inversează

noi tu să îl obținem pe x x va

fi egal cu 12 ori 10 supra 15 adică

120 supra 15 are este egal cu 8

Deci lucrarea se va termina în

opt zile