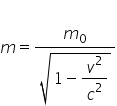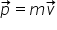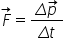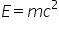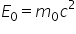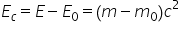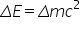Masa relativistă. Relaţia masă-energie: ecuaţia Einstein.
Tag-uri
Partajeaza in Google Classroom

Transcript
în cea de a șasea și ultima Lecție
despre teoria relativității restrânse
vom discuta despre dinamica relativista
și despre ecuația dezvoltarea dinamicii
relativiste pleacă de la Red Definirea
conceptului de masă Dacă va aduceți
aminte în mecanica clasică newtoniană
dinamica Începe prin introducerea
conceptului de masă a unui sistem
fizic care era legat de proprietatea
lui de inerție și apoi de conceptul
sau mărimea vectorială forță Ce
descrie acțiunea unui corp asupra
altui corp ce era legată de masă
și accelerație prin ecuația fundamentală
a mecanicii newtoniene Antonie
ne forță egal cu produse dintre
masă și accelerația de asemeni
se introduceau parametrii precum
impulsul care era produsul dintre
masă și viteză prin definiție și
prin consecință variația impulsului
în unitatea de timp era egală cu
forța și de asemeni se introducea
energia unui sistem fizic sau unui
corp care era masa ori viteza la
pătrat împărțit la 2 plus energia
potențială si depinde de tipul
de interacțiuni care sistemul fizic
sau corp era implicat acestea erau
noțiunile de bază din mecanica
clasică mecanica relativista stăm
pleacă de la definiția impulsului
unui corp saună sistem fizic care
rămâne aceeași ca aceea din mecanica
clasică Deci plecăm de la definiția
impulsul este egal cu masa ori
viteza și mai important legea de
conservare a impulsului și anume
În absența unor forțe externe impulsul
se conservă în sisteme de referință
inerțial adică de accelerație rămâne
valabilă de aici observăm imediat
că în mecanica relativista masa
trebuie să fie redefinit într o
transformare Lorenz pe care tocmai
am văzut o compunerea vitezelor
se schimbă și în consecință pentru
a păstra aceleași proprietăți ale
impulsului masa trebuie să aibă
o altă să fie dependentă de viteză
și să aibă o altă comportare fără
a face o derivare acestei ecuații
în cinematica relativista se poate
demonstra că masa unui sistem sau
unui corp în sistem de referință
inerțial aflați în mișcare este
egală cu masa de repaus adică masă
în sistemul de referință inerțial
propriu cel legat de stimul fizic
considerat împărțit la 1 minus
b pătrat pe ce pătrat sau altfel
spus m este egal cu gama m 0 din
nou de mă ceartă formulă foarte
importantă fără Demonstrați o consecință
esențială este aceste formule este
că în mecanica relativista masa
nu mai este o constant masa pe
care bineînțeles o măsurăm tot
în kilograme depinde de viteza
de deplasare a corpului Care este
măsurată în metri pe secundă în
felul următor avem o valoare egală
cu m0 cu masă în sistemul de referință
propriu pentru orice viteză care
este mică sau Mady totuși Când
ajungem la viteze foarte mari comparabile
Cu ce viteza luminii în vid adică
300.000 de km pe secundă dintr
o dată masa de bine de vinete pandant
de viteză și obținem această dependență
Deci din nou masă este constantă
pentru viteze mici medii sau chiar
suficient de mari Dar când ajungem
la viteză de ordinul zecilor de
mii de kilometri pe secundă Deci
viteze extraordinare dintre odată
ma să încep să devină puternic
dependent de viteza sistem relația
fundamentala a dinamicii rămâne
adevărat în raport cu impulsul
dar nu și în raport cu accelerația
adică putem în continuare spune
că Forța este variația impulsului
raport cu timp Deci aveam această
definiție care ducea la această
relație dintre Impuls și forțăm
iar rămâne valabilă în mecanica
relativista ce nu mai este adevărat
este relația fundamentală ecuația
fundamentală f egal cu Ema nu mai
este adevărată și aceasta putem
vedea din această ecuație adică
e Forța F va fi egală cu de la
DT derivat derivat aeroport cu
timpul a impulsului Care este mv
adică este de la DT din m0 gama
V dar amândouă atât gama cât și
v sunt dependente de timp deci
obținem doi factori și anume avem
un m0d gama la DT de gama la de
ten mulți cu v plus un al doilea
termen care este în zero gama de
valide T Care este accelerația
Deci vedem că obținem o ecuație
mai complicată a forței în mecanica
relativista de asemeni bineînțeles
principiul corespondenței funcționează
adică pentru viteze mult mai mic
decât c în acest regim de viteze
masa gama de Vine Egal cu aproximativ
egale cu 1 Decembrie vine aproximativ
egale cu m zero ceea ce înseamnă
că recuperăm ecuațiile din mecanica
clasică pentru Impuls și forța
în fizică relativă stăm accelerația
și forța devin mărimi secundare
asta înseamnă că bineînțeles le
putem calcula și ne putem folosi
dar devin secundare ele fiind înlocuind
înlocuite de mărimile impulse energie
și intensitatea Câmpului pentru
motive asupra cărora nu insist
ele se comportă diferit la transformările
lorentz să trecem la următoarea
etapă în dezvoltarea mecanicii
relativiste și anume energia energia
relativista ecuația pentru energia
relativista se numește ecuația
Einstein explicație faimoasă și
îți ia Stabilește relația dintre
masa relativă stă și energie relativă
stă fiind în modul cel mai simplu
următoarea a egal cu MC pătrat
aceasta Stabilește o relație directă
între negii și masă pentru că ce
pătrat este bineînțeles o constantă
de această ecuație fără de demonstrație
mod evidentia se poate demonstra
plecând de la principiile Einstein
și transformările lorentz dar demonstrație
este complicată și nu voi sta cerută
dumneavoastră deci numai o dăm
fără demonstrație și discutăm implicațiile
ei în primul rând asta înseamnă
că vom avea o energie de repaus
energia unui sistem sau unui corp
în sistemul de referință propriu
Ia să văd Lacul iezerul și va fi
egală cu masa de repaus înmulțită
cu sila pătrat de asemeni implicații
este că orice variație a energiei
însoțită de o variația masei și
invers pur și simplu din nou pentru
că Ce pătrate o constantă Deci
dacă e variază singur fel în care
o poate face este printr'o variația
lui m de asemeni putem defini și
definim energia cinetică relativista
ca diferența dintre energia în
sistemul de referință propriu al
0 și energia în orice alt sistem
de referință asta pentru că în
sistemul de referință propriu bineînțeles
prin definiție corpul sau sistemul
este în repaus și el se află în
mișcare nu orice alt sistem de
referință inerțial deci diferența
dintre sistemul de referință propriu
și asistent de referință este mișcarea
În consecință diferența dintre
energiile între cele două energii
va fi o energie cinetică Și de
ce nu desene este egală cu a minus
n 0 munții cu Cela pătrat în fine
un alt comentariu este legat de
principiul de corespondență și
anume se poate demonstra că în
limita vitezelor mult mai mici
decât viteza lui vide această ecuație
să reducem la ecuația binecunoscută
în mecanica newtoniana pentru energia
cinetică și anume 1 pe 2 m 0 pătrat
masa de repaus înmulțit cu viteză
la pătrat nu vom demonstra această
deducție numai în treacăt să spunem
că ea pleacă de la faptul că pentru
V mult mai mic decât c se poate
aproxima factorul gama ca fiind
1 plus z pătrat împărțit la 2 si
pătrat Până acum am spus că în
această limită gama este aproximativ
egale cu 1 și asta Rămâne în continuare
adevărat pentru că acest această
corecția ce să fac tradițional
care îl am adăugat este în limita
avem mai mic decât c egal cu 0
Dacă vei mult mai mic decât c atunci
cu atât mai mult Vei pătrat va
fi mult mai mic decât doi Ce pătrate
știind de la zero totuși se poate
demonstra folosind o așa numită
expansiune între o serie Taylor
a lui gaman cazul acesta această
formulă plecând de la această formulă
se poate deduce imediat această
aproximație În limita vitezelor
mici pentru energia cinetică relativista
Care este energia cinetică a mecanica
clasică un ultim comentariu este
legătura dintre masă și energie
implicată de ecuația asta și anume
în modul cel mai direct și profund
ecuația Einstein implică că masa
se transformă în energie energia
se transformă în masă și astfel
masă Este o formă particulare de
energie trebuie să menționez la
acest moment că manual dumneavoastră
ce puțin manualul pe care îl am
eu în față de fizică clasa a 12-a
firmă contrarul și anume că nu
ar trebui să interpretăm ecuația
Einstein Hai implicând o echivalență
amasi cu energiei în sensul că
ele se pot transforma un antral
Tom eu a fim contrarul din fizică
a pe care o știu eu și am învățat
eu ecuația niște implică exact
acest lucru mai mult pot să și
dau exemple în care acest lucru
se întâmplă în universul din jurul
nostru în particular anumite ramuri
ale fizicii și anume fizica subatomică
fizica cuantică fizică nucleară
astrofizica abundă În astfel de
procese în care masă se transformă
în energie masa de repaus în particular
și un astfel de exemplu este următorul
un proces în care două particule
numite fotoni despre care vom vorbi
imediat își în lecțiile următoare
vom introduce particula numită
photo on în două sau trei lecții
de acum încolo Deci doi fotoni
se combină formând un electron
și o altă particulă numită pozitron
ce are aceeași masă ca și electronul
deci dacă vreți din punct de vedere
al masei 2 fotolii se combină în
doi electroni la fel un electron
și un pozitron se combină și dispărând
formând USA în faza finală a acestui
Proces în starea finală simplu
înspre acest doi fotoni de ce aceste
procese sunt foarte importante
în particular acest proces ne spune
că în starea inițială avem o formă
de energie numai saghi numai formă
de masa de repaus Deci avem doi
electroni foarte apropiați cu masa
2 m 0 unde îmi 0 este masa de repaus
a electronului și nu avem o negi
cinetică iar în faza finală avem
o masă 0 fotonii plin definiție
au masa de repaus 0 și în acest
proces se vor avea o energie cinetică
Deci avem în consecință o transformare
directă a masei de repaus în stare
inițială în energie cinetică în
starea finală poate și mai relevant
un alt fel de proces este următorul
există o particulă nu contează
exact Care sunt proprietățile ei
dar există o particulă care se
numește pi zero care este instabilă
Deci după un anumit timp se dezintegrează
Deci acest pe zero stând pe loc
stând în repaus se dezintegrează
în doi fotoni ce este important
din nou este că acest paese.ro
are o masă destul de mare pentru
lumea subatomică deci aproape o
șeptime din masa atomului de hidrogen
este masa acestui pe 0 Deci avem
o masa de repaus semnificativă
în stare inițială și nu avem o
energie cinetică în starea finală
obținem din nou 2 fotoni Asta înseamnă
din nou masa de repaus 0 și energie
cinetică singura concluzie posibilă
este că avem o transformare a masei
de House în energie cinetică un
alt proces care foarte important
care vine din alta ramura a fizicii
și anume astrofizica se referă
la radiați electromagnetică produsă
de soare și vor cealaltă stea în
fazele principale ale folosirii
unei stele care are loc prin procesul
de fuziune nucleară în particular
avem un nucleu de hidrogen și un
alt nucleu al de Triton Deci H2
plus H3 adică hidrogeni cu masa
2 și hidrogen cu masa 3 fuzionează
se combină și rezultă un nucleu
de heliu și Oradea și electromagnetică
Adică o particulă numită Foton
după cum se vede în acest proces
are loc o pierdere de masă din
chimie știm că acest număr este
masa atomică a Deci avem o masa
atomică totală egală cu 5 în stare
inițială ce egal cu 4 în starea
finală avem o pierdere de masă
și avem o că și tu un câștig de
energie pentru că acest fotoliu
a Stării Oxid din acest proces
cu energie cinetică substanțial
acesta este procesul cel mai important
nu singurul dar ce mai important
prin care o stea și în particular
soare în Oare lan ostru produce
energie pe care apoi explodează
în spațiu și Spre exemplu o recepționăm
noi pe pământ sub formă de radiație
electromagnetică adică foto