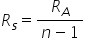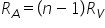Măsurători electrice.
Tag-uri
Partajeaza in Google Classroom

Transcript
În ce an a 9-a Lecție despre curentul
electric continuum vom discuta
despre măsurări electrice adică
despre măsurarea intensității curentului
și rezistenței electrice curentul
intensitatea curentului electric
se măsoară bineînțeles cu un ampermetru
de multe ori dorim să mărim domeniul
de măsurare al unui ampermetru
și pentru a mări acest domeniu
de utilizare de n ori adică pentru
a putea măsura curenți cu intensități
de până la n ori mai mari decât
intensitatea maximă permisă pentru
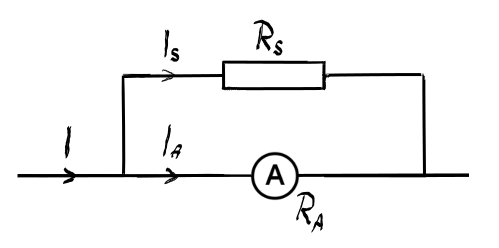
arme ampermetrul nostru se conectează
în paralel cu ampermetrul un sunt
Care este o rezistență dormită
valoare Haide să calculăm valoarea
acestei rezistențe RS a șutului
pentru calm curentul măsurat de
ampermetru e a să fie de 10 ori
mai mic decât curentul ce trece
prin această placeți conductor
Deci putem Scrie prima lege circov
pentru acest Nord să notăm nodul
m și vom avea curenții curentului
care intră și curenții Așii esti
prima lege circo pentru nodul m
se scrie e este egal cu e a cruceas
și după ca ma sus dorim ca curentul
e să fie de n ori mai mare decât
curentul măsurat de către ampermetru
ia înlocuind obținem că e n minus
unu e a este egal cu s din legea
ohm pentru această porțiune de
circuit m n putem scrie că you
Care este diferența de potențial
dintre punctele m și n este egal
cu r a i a și este egal de asemeni
cu r s e s folosind aceste două
relații obținem că e n minus 1
împărțit la r a este egal cu împărțit
la aer adică relația finală care
o căutam r s este egal cu r a împărțit
la n minus 1 aceasta este valoarea
rezistenței șutului în raport cu
rezistență ampermetrului pentru
care obținem o amplificare de n
ori a domeniu de măsurare ampermetru
în practică Spre exemplu dacă avem
o rezistență ampermetrului de 0
1.000 și curentul maxim al ampermetrului
nostru este 10 amperi dar dorim
să putem măsura până la 100 de
amperi 100 de amperi Adică n este
10 pui și simplu înlocuim în relația
de mai sus și obținem că trebuie
să folosim în paralel cu ampermetrul
sunt cu rezistența egală cu 0 1.000
împărțit la 9 adică 10 minute nu
deci 0 RON dacă facem aceasta Spre
exemplu Când ampermetrul va măsura
să zicem 3 amperi asta înseamnă
că curentul prin conductor este
de fapt 30 de amperi tensiunea
electrică se măsoară bineînțeles
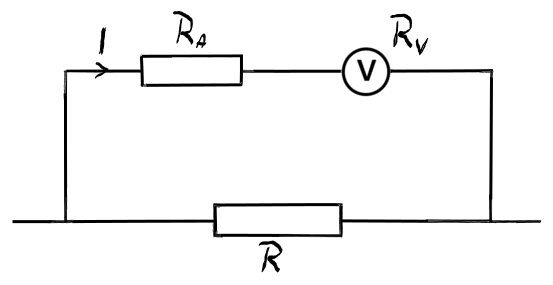
cu un voltmetru la fel putem extinde
domeniul de măsurare al voltmetrului
V ce măsoară tensiunea la bornele
rezistenței rezistenței r dacă
folosim o altă rezistență numită
rezistența adițională în serie
cu voltmetrul pentru a crește tensiunea
maximă de n ori relația pe care
nu putem scrie mediat este că un
este egal cu u a plus Deci tensiunea
dintre punctele sale notăm tot
cu m și n va fi diferența de potențial
rezistența adițională plus rezistența
de potențial măsurat diferența
de potențial măsurată de voltmetru
nostru după cum am spus dorim ca
să fie de n ori UV adică tensiunea
sau diferența de potențial măsurată
de v să fie de n ori mai mică decât
diferența de potențial de pe rezistor
în concluzie putem scrie că e n
minus 1 este egal cu u a împărțim
prin concurentul comun Deci avem
același curent ce trece prin rezistența
adițională și volumul obținem că
iar a este egal cu n minus 1 r
v Deci din nou am împărțit la aceasta
este valoarea pentru rezistența
adițională comparată cu rezistența
voltmetrului pentru care putem
extinde de n ori domeniul de măsurare
al volumului să trecem la măsurarea
rezistenței pentru măsurarea rezistenței
electrice se folosesc două metode
prima metodă implică utilizarea
unui ampermetru și a unui voltmetru
iar cea de a doua metodă implică
utilizarea unei punți de rezistoare
începem cu metoda ce folosește
combinația voltmetru ampermetru
pentru măsurarea unei rezistențe
cu valoare mare de chiar în acest
desen este rezistență cu valoare
mare folosim un ampermetru și un
voltmetru celălalt element al acestui
circuit este generatorul G de ce
în acest caz putem aplica cea de
a doua legea lui chircov pentru
acest ochi Deci în acest ochi uite
îmi scrie că avem este egal cu
u a plus e a r adică altfel spus
tensiunea dintre punctele m și
n este egală cu tensiunea măsoară
Deva metru și este egală cu suma
dintre tensiunea la bornele ampermetrului
plus tensiunea la bornele rezistorului
de aici rezultă că aer este egal
cu cu A minus scuzați u z minus
u a împărțit la ei adică este egal
cu UV împărțit la ei minus r a
rezistența ampermetrului raportul
dintre tensiunea la bornele ampermetrul
și intensitate i a a este curentul
comun ce trece prin această ramură
a ochiului Deci raportul dintre
ua și ia este rezistența ampermetrului
dar am spus că ne aflăm în cazul
în care rezistența El e mare Asta
înseamnă că îmi particulare stent
ampermetrului este mult mai mică
decât aer ne aflăm în acest caz
de Ce rezultă de aici că aer este
aproximativ egale cu UV împărțit
la ia să notăm că în general un
ampermetru are rezistență mică
și dacă în particular în cazul
nostru rezistența R este mare această
relație este satisfăcută deci pur
și simplu citim tensiunea din de
pe voltmetru și intensitatea de
pe ampermetru și raportul lor este
rezistența iar dacă rezistența
în schimb este mică și de se apropie
de valoarea rezistenței ampermetrului
trebuie să modificăm un pic montajul
adică circuitul electric și folosim
în așa numit montaj amonte în care
avem aceeași același timp de montaj
dar voltmetrul este în paralel
doar cu rezistența nu cu rezistența
și ampermetru în acest caz Putem
să scriem din prima lege a lui
chircov că e a este egal cu e z
plus ia unde în mod Evident e a
este intensitatea curentului prin
ampermetru este intensitatea curentului
prin voltmetru și e r este intensitatea
curentului prin rezistenta pe care
dorim să măsurăm acest această
ecuație se poate scrie mai departe
ca un V împărțit la r m Plus cu
plus aer împărțit la Dar bineînțeles
deoarece sunt în paralel cu v este
egal cu cu Da volumul este în paralel
cu rezistența aer Deci pensiunile
de la bornele lor sunt egale cu
diferența de potențial dintre punctele
m și n rezultă că e a este egal
cu UV înmulțit cu 1 pe Hervis 1
pe r dar după cum am spus ne aflăm
în cazul în care el este mic de
cer este mult mai mic decât acesta
este adevărat atât pentru că este
mic dar și pentru că în general
sau întotdeauna voltmetrele au
rezistențe mari în general ampermetrelor
rezistenței mici și volumele o
rezistență ma Deci dacă ieri Este
mic și îl vezi de mare atunci el
este mult mai mic decât b și în
concluzie putem scrie că r este
aproximativ egale deci putem să
neglijăm acest termen și deci el
va fi aproximativ egale cu cu v
împărțit la ia iar este raportul
dintre tensiunea ciuci pe care
o citim pe voltmetru împărțită
la intensitatea pe care o citim
pe ampermetru cele doua metodă
este metoda funcțiilor de rezistențe
în particular cea mai folosită
Este așa numită punte weston puntea
wheatstone pe care o vedeți în
acest desen este o aplicație practică
a metodei 0 de măsurare a unei
mărimi prin care în loc să măsurăm
direct cu mărimea mărimea de interes
în cazul nostru rezistența RX dorim
să măsurăm valoarea rezistenței
rx1 să măsurăm direct o mărime
de interes precum această rezistență
măsură Mai degrabă o diferență
de mărimi citind de la zero adică
ia valori foarte mici o astfel
de măsurare adică măsurarea unei
diferențe de Valori in general
mai precisă pentru că erorile de
măsurare se simplifică prin operația
de scădere când măsurăm o rezistență
întotdeauna în practică în Deci
dacă măsurăm o valoare aer întotdeauna
vom avea o eroare de măsurare Delta
EUR dacă măsurăm Air 1 minus ar2
în loc să măsurăm un aer această
eroare de măsurare se va simplifica
când se măsoară diferența de aceea
metoda 0 și o metodă în general
mai precis cum facem acesta folosim
acest instrument numit galvanometru
De ce nu mai este un generator
în acest desen și un galvanometru
galvanometrul notat cu Jean acest
desen e un ampermetru sensibil
la intensități ale curentului foarte
mici de ordinul micro amperului
micro înseamnă de ordinul 10 la
minus 6 amperi practic măsurarea
a reloca să se variază rezistența
etalonul Deci acest aer este o
rezistență variabilă se va realiza
acest până când intense obținem
o intensitate prin galvanometru
egală cu 0 Deci aer se variază
astfel încât să obținem un egal
cu 0 egal cu 0 înseamnă evident
că între punctele m și n nu avem
nicio diferență de potențial Deci
v m m egal cu v Pe de altă parte
dacă notăm curenții e 2:01 putem
scrie imediat că avem următoarele
relații va minus v m este egal
cu Eric Si 2 de asemeni vm minus
v b este egal cu re2 asta deoarece
curentul e g este egal cu 0 când
puncte este în echilibru și Deci
curentul prin aer va fi egala tunci
cu curentul prin Eric și va fi
E2 de asemeni pe celălalt traseu
între punctele a și b avem că va
minus v e n este egal cu r11 și
v n minus v b este egal cu r21
din aceste relații și folosind
faptul că de fapt când puncte este
echilibrată vm este egal cu vn
putem scrie în sfârșit că ar xe2
este egal cu r11 dar și că re2
este egal cu her-2 Ion din nou
pentru că BM egal cu Van Deci obținem
aceeași cantitate în această parte
a ecuațiilor Deci acestea două
de vin egală la fel v m egal cu
vand Deci acesteia două devin egale
făcând raportul pentru a elimina
curenții obținem că r x împărțit
la R este egal cu R 1 împărțit
la r 2 deci RX rezistența pe care
dorim să măsurăm va fi unul împărțit
la r 2 înmulțit cu r valoarea rezistenței
variabile și să îl acesta se folosește
puntea weston Pentru a măsura valoarea
rezistenței necunoscute RX