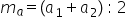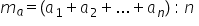Media aritmetică a două sau mai multe numere naturale

cum vorbim continuare despre Media

aritmetică a două sau mai multe

numere naturale cred că deja ați

auzit vorbind nu se dă spre media

aritmetică pentru că ea se folosește

la școală la calculul medii anuale

sau și la calculul mediei semestriale

pentru materiile la care nu se

dă teză să știți că media aritmetică

se folosește și în statistică și

haide să dăm un exemplu să vedem

cum ce exprimă media aritmetică

și luăm un șir de numere 1 și relator

de numere naturale 2 5 9 7 și 3

Deci am ales cinci numere naturale

putem să alegem oricât de multe

voia Ce înseamnă să calculăm media

aritmetică cum am notat media aritmetică

pe avem aici un an și un an mai

mică acesta a mai mic se numește

indice Deci avem m indice a ca

să calculăm media aritmetică a

unui șir de numere facem în felul

următor adunăm numerele din șirul

respectiv Deci doi plus cinci plus

9 plus 7 plus 3 și această sumă

o împărțim la Câte numere sunt

în șir b Câte numere avem unu doi

trei patru cinci numere de împărțim

la cinci acest calcul reprezintă

de fapt media aritmetică cid să

vedem ce obține facem suma avem

aici 10 cu 9 1919 cu Șapte caiete

de 7 obținem 26 împărțit la 5 bun

Nu o să facem acum o împărțire

cu rest ce o să scriem rezultatul

ca număr zecimal și o să obținem

5 ca prima observație putem să spunem

că deși am avut în acest șir doar

numere naturale iar dacă media

aritmetică Mitică valoarea pe care

am obținut un număr natural deci

nu e neapărat să obținem valoarea

mediei aritmetice număr natural

deși avem niște numere naturale

poate să fie număr natural sau

poate să nu fie număr natural bun

o altă observație pe care o putem

face este aceea că media aritmetică

reprezintă tendința centrală a

unui șir de numere iar dacă vom

muta acest șir în ordine crescătoare

trecem numărul doi urmează apoi

trei cinci și șapte și nouă ani

și 10 numere în ordine crescătoare

Ce observăm că numărul care se

află să spunem așa în mijlocul

șirului adică 5 este apropiat ca

valoare de media aritmetică de

acest lucru ne arată faptul că

media aritmetică exprima tendința

centrală a acestui șir de numere

însă foarte mare atenție acest

lucru nu se întâmplă pentru orice

șir de numere ci doar pentru acele

șiruri în care numerele date în

șir sunt apropiate între ele ca

valoare dacă am fi avut de exemplu

și un alt număr mai mare să spunem

300 atunci tendința centrală a

șirului respectiv nu ar fi fost

descrisă prin media aritmetică

și prin alte metode totuși vom

spus acest lucru și am făcut și

această observație ca să vă faceți

Câte câte o idee legată de media

aritmetică ce putem însă să spunem

Cu siguranță e urmatorul lucru

întotdeauna media aritmetică este

mai mare sau egal decât cel mai

mic număr al șirului pe care îl

putem exprima astfel minimul și

notăm aici numerele din șir 2 5

9 7 și trei și media aritmetică

este mai mică sau egală întotdeauna

decât valoarea maximă a șirului

de notăm Max și scriem numerele

din șir 2 5 9 7 și 3 Păi Haideți

să vedem dacă e așa care e cel

mai mic număr din șir 2 este 2

mai mic sau egal cu 5 adică cu media

aritmetică este 5 la rândul său

este mai mic sau egal decât cel

mai mare număr din șir Adică decât

9 este Deci acest lucru întotdeauna

are loc media aritmetică este cuprinsă

între cel mai mic număr al șirului

și cel mai mare Haideți acum să

facem și media aritmetică a două

numere și avem numerele 7 și 39

vrem să calculăm media lor aritmetică

cum vom proceda Păi trebuie să

adunăm numerele 7 plus 39 iar Suma

obținută trebuie să o împărțim

la Câte numere sunt pe avem unu

două două numere Deci împărțim

la doi cât obținem 7 cu 39 ne dă

46 împărțit la 2 palme obține 23

pe apă când această situație media

aritmetică este un număr natural

acum Haideți să vedem media aritmetică

a Dică numărul 23 este cuprins

între cel mai mic număr al șirului

și cel mai mare număr al șirului

cel mai mic număr din acest șir

este 70 nu putem să numim șir de

numere Avem doar două numere 7

este mai mic sau egal cu 23 și

23 la rândul său este mai mic sau

egal decât 39 bun Dacă am vrea

acum să scriem o formulă atunci

dacă avem două numere 60 să le

notăm așa cu a indice 1 și a indice

2 deci Avem două numere naturale

ca să calculăm media lor aritmetică

ce vom face adunăm aceste numere

și apoi Suma obținută împărțind

la Câte numere sunt Păi avem două

numere Deci împărțim la doi Deci

am obținut formula mediei aritmetice

pentru două numere dacă avem trei

numere a indice 1 a indice 2 și

a indice 3 la fel trebuie să adunăm

cele trei numere și suma împărțim

la Câte numere sunt adică unul

doi trei numere formula mediei

aritmetice pentru trei numere naturale

și așa mai departe dacă avem n

mic numere naturale adică a indice

1 a indice 2 este al doilea număr

și așa mai departe până la a indice

n l n la număr ca să calculăm media

aritmetică procedăm la de adunăm

facem suma Haideți să facem în

așa fel încât să se vadă Semnul

plus Deci facem suma și o împărțim

la Câte numere sunt pe Câte numere

avem primul număr al doilea al

inele număr de ce împărțit la n

mic pentru că sunt în mic numere

naturale și notăm aici formula

mediei aritmetice pentru n numere

naturale Haideți acum să aplicăm

ce am învățat la finalul primului

semestru Dana are la geografie

următoarele note 10 7:10 și trebuie

să vedem Care este media la geografie

Pe primul semestru unde Dan a obținut

aceste note nu avem teza Deci nu

vom nota nimic aici ce avem de

făcut ca să calculăm media Am calculat

media aritmetică a acestora numere

și avem 10 adunat cu 7 avem trei

numere adunat cu 10 astăzi sumă

o împărțim la Câte numere sunt

și avem unu doi trei deja Voiam

să scriu trei deci media aritmetică

este egală cu și vom obține aici

27 împărțit la trei Deci avem nouă

cu alte cuvinte venim și notăm

Dana a obținut Pe primul semestru

la geografie media 9 altă problemă

în acest tabel avem notate temperaturile

citite la ora 9:00 în primele cinci

zile ale săptămânii de luni până

vineri și vrem să vedem care este

temperatura media primelor acestor

cinci zile sau altfel spus Care

este media acestor 5 temperaturi

ce avem de făcut Trebuie să adunăm

aceste temperaturi Deci calculăm

media aritmetică și vom aduna 15

cu 13 cu 9 cu 12 și cu 16 această

sumă o împărțim la Câte numere

sunt pe avem cinci zile de 5 temperaturi

împărțim la cinci și media aritmetică

este egală cu facem suma avem aici

2813 cu 9 ne dă 22 adunând aici

obținem 50 cu 15 Deci 65 bun am

65 împărțit mai departe la cinci

și obținem că media aritmetică

este 13 cu alte cuvinte temperatura

sau media temperaturilor primelor

cinci zile ale acestei săptămâni

la ora 9:00 este de a fost de 13

grade Celsius putem să verificăm

și aici inegalitatea discutată

și anume media aritmetică adică

numărul 13 este cuprins între cel

mai mic număr dintre acestea care

cel mai mic 9 și cel mai mare număr

dintre ele adică 16 la 13 este

cântat adevăr cuprins între nouă

și 16 vreau să mă mai arat încă

două tipuri de probleme pe care

le puteți întâlni și primul tip

este acesta media aritmetică a

șase numere este 95 Care este suma

numerelor pe Haide să notăm aceste

șase numere cu a indice 1 primul

număr a indice 2 al doilea a indice

3 a indice 4 a indice 5 și a indice

șase Clarke avem șase numere știind

că media lor aritmetică este 95

și trebuie să găsim suma acestor

numere pe Haide să scriem formula

mediei aritmetice pentru șase numere

Deci adunăm toate numerele iar

suma o împărțim la Câte numere

sunt Adică la 6:00 ce am notat

Aici este formula mediei aritmetice

pentru șase numere bun Ce știm

noi acum că această media aritmetică

este egală cu 95 Deci toate această

expresie pe care Haideți o copiem

Buna am copiat ore este egal mai

departe cu 95 atât ai media aritmetică

ce ne interesează pe noi suma acestor

numere adică exact această sumă

cariată apare aici Păi această

sumă Haideți să o notăm cu s mic

de la sumă și vrem să determinăm

Pass Păi ce știm știm că ies împărțit

la 6 este egal cu 95 cu alte cuvinte

Am obținut o ecuație cu necunoscuta

esti asta înseamnă că ies Cu cât

este egal pe Ce număr împărțit

la 6 ne dă 25 95 înmulțit cu 6

și vom obține 6 ori 5 3003 nu mint

șase ori 954 cu 357 Deci suma este

egală cu 570 iar dacă pentru a

semenea probe vreme în care ni

se dă media aritmetică a unor numere

știind Câte numere sunt foarte

ușor să determinăm suma acelor

numere om obține până la urmă o

ecuație în care necunoscută esti

chiar suma cerută un alt tip de

problema Media aritmetică a două

numere este 14 știind că unul dintre

numere este egal cu 3 sau flămând

celălalt număr bim acum de două

numere și știm că media lor aritmetică

este 14 Ce mai știm că iată că

unul dintre numere este egal cu

3 și trebuie să găsim celălalt

număr Păi Haideți să notăm numărul

căutat cu x o altă cuvinte Avem

două numere avem numărul 3 și numărul

x știind că media lor aritmetică

este 14 Deci 3 plus x împărțit

la câte numere avem vrem să scriem

media acestor două numere este

egală cu media aritmetică a Dică

scriem direct 14 bun și acum trebuie

să determinăm pe x iată că am obținut

o ecuație foarte simplă Haide so

rezolva mai întâi Ce trebuie să

găsim trebuie să vedem care este

valoarea acestei sume Ce număr

împărțit la 2 ne dă 14 Păi ca să

aflăm acest număr adică 3 plus

x înseamnă că pe 14 trebuie să

îl înmulțim cu 2 și avem că trei

adunat cu X ne dă 28 e ușor de

văzut că x este egal cu 28 minus

3 Deci 25 acesta este răspunsul

evident că putem să facem și verificarea

cu alte cuvinte vedem dacă media

aritmetică a numerelor 25 și 3

este întradevăr egală cu 14 Păi

25 plus 3 împărțit la câte numere

avem adică la 2 ne dă 28 împărțit

la 2 adică 14 Iar avem o relație

adevărată