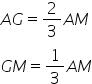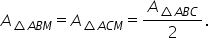Mediana în triunghi

mediană în triunghi înainte de

a vorbit despre mediană Haideți

să ne reamintim Ce linii importante

în triunghi am învățat până acum

fiind dat în triunghiul oarecare

abc am văzut că bisectoarea este

o semidreapta care împarte un unghi

al triunghiului în două unghiuri

congruente dacă a m este bisectoare

măsura unghiului b a m va fi egală

cu măsura unghiului m a c o ață

linii importante în triunghi este

mediatoarea mediatoarea segmentului

BC este perpendiculară ridicată

din mijlocul segmentului Așadar

punctul D este mijlocul segmentului

b c iar d e f este o perpendiculară

pe BC apoi am discutat despre înălțime

înălțimea este perpendiculară adusă

dintre un vârf al triunghiului

pe latura opusă acum să vedem ce

este mediană mediană este segmentul

care unește vârful triunghiului

cu mijlocul laturii opuse o să

dăm și definiția mediană în triunghi

este segmentul care unește un vârf

al triunghiului cu mijlocul laturii

opuse În triunghiul ABC a fixat

mijlocul laturii BC pe care la

mutat cu d a d se va numi ne Diana

dacă BD este congruent cu DC adică

D este mijlocul segmentului BC

atunci ad se numește mediană având

în vedere că un triunghi are trei

vârfuri și trei laturi putea construi

trei mediane aceste trei mediane

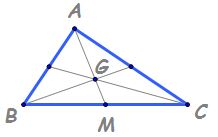
se vor intersecta întru un punct

pe care îl notăm de obicei cu g

și acesta se va numi centrul de

greutate al triunghiului acest

centru de greutate are proprietatea

că este situat pe fiecare mediană

la o treime de bază și la două

treimi de vârf mai exact lungimea

segmentului g d este o treime din

ad iar lungimea segmentului AG

este două treimi din mediană ad

matinale o să mai dăm o proprietate

a medianei întru în triunghi mediană

împarte un triunghi în două triunghiuri

de arii egale 8 spune că două triunghiuri

care au ariile egale se pot numi

triunghiuri echivalente avem un

triunghi oarecare abc am construit

mediană dusă din vârful a Va trebui

să demonstrăm că cele două triunghiuri

care sau format au ariile egale

scrie mai întâi ipoteza fiind dat

un triunghi abc oarecare și un

punct d situat pe latura b c astfel

încât BD să fie congruent cu DC

trebuie să arătăm că aria triunghiului

ABD este egală cu aria triunghiului

adc nu am demonstrat ceastă proprietate

să evidențiem mai bine cele două

triunghiuri este vorba de triunghiul

ABD și adc ne reamintim că aria

unui triunghi în general este egală

cu baza ori înălțimea supra 2 Haideți

atunci să exprimăm aria triunghiului

ABD mai întâi va trebui să construim

înălțimea în acest triunghi voi

construi o perpendiculară din A

pe BD aceasta este a m nu scrie

că aria triunghiului ABD este egală

cu baza adică BD ori înălțimea

corespunzătoare ei a m supra 2

aria celuilalt triunghi abc va

fi egală cu baza BC înălțimea corespunzătoare

laturii BC este tot a m pentru

că a m este perpendiculară pe latura

DC dar știm din ipoteză că BD este

congruent cu DC pentru că de este

mijlocul segmentului BC deci lungimea

segmentului BD este egală cu lungimea

segmentului De ce din aceste trei

relații observăm că aria triunghiului

a b d va fi egală cu aria triunghiului

adc Așadar rețineți că o mediană

împarte un triunghi în două triunghiuri

având aceeași arie în continuare

o să facem o aplicație Fie abc

un triunghi oarecare Să se arate

că distanțele de la b și c la mediană

a d sunt egale alte cuvinte mediana

a d este egal depărtat de punctele

B și C desenam în triunghiul oarecare

a b c ducem mediană ad unde d este

mijlocul segmentului BC și va trebui

să construim distanțele de la b

și c la mediană a d vreau mintesc

că distanța de la un punct la o

dreaptă este perpendiculară adusă

din acel punct pe dreaptă Așadar

cu ajutorul echerului vom duce

o perpendiculară din b pe AD în

să observăm că pentru a construi

perpendiculara din c pe a d va

trebui să prelungim segmentul ad

am prelungit segmentul ad și am

dus b m perpendiculară pe a d și

c n perpendiculară pe AD trebuie

să arătăm că BM este congruent

cu CN mai întâi vom scrie ipoteza

și concluzia avem un triunghi abc

oarecare un punct d care aparține

laturii BC Asta e încât b d să

fie egal cu DC ma trebui să arătăm

că distanța de la punctul B la

mediană a d este egală cu distanța

de la punctul c la mediană ad adică

mediană va fi egal depărtate de

punctele B și C demonstrație anunțăm

și construcțiile pe care le au

făcut am dus BM perpendiculară

pe a d înseamnă că distanța de

la B la ad este bem apoi am construit

si n perpendiculară pe a d rezultă

că distanța de la c la a d va fi

ce an mai trebui să arătăm că b

m și c n sunt congruente pentru

a demonstra congruență a doua segmente

le încadrăm în două triunghiuri

a căror congruență poate fi demonstrată

o să comparăm triunghiurile b m

d și c ND observăm că acestea sunt

triunghiuri dreptunghice Deci va

fi suficient să găsim două elemente

congruente ale acestui triunghiuri

știm din ipoteză că BD este congruent

cu DC din ipoteză și observăm că

unghiurile m d b și si de n sunt

unghiuri opuse la vârf Deci vor

fi și acestea unghiuri congruente

unghiul b d m este congruent cu

unghiul c d n fiind unghiuri opuse

la vârf din cele două relații rezultă

conform cazului de congruență ipotenuză

unghi pentru că b d și c d sunt

ipotenuze în cele două triunghiuri

dreptunghice rezultă că triunghiul

b d m este congruent cu triunghiul

cdn iar congruență acestor două

triunghiuri implică și congruența

segmentelor BM și CN Așadar distanța

de la punctul B la mediană a d

va fi egală cu distanța de la punctul

c la mediană a d