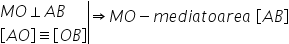Mediatoarea unui segment

mediatoarea unui segment concurența

mediatoarelor laturilor unui triunghi

Mediatoarea unui segment este perpendiculară

dusă Prin mijlocul segmentului

pentru a construi mediatoarea unui

segment avem nevoie de un liniar

shaker desenam un segment AB apoi

fixă mijlocul acestui segment pe

care îl am notat cu m și cu ajutorul

echerului ridicăm o perpendiculară

pe latura ab perpendiculară este

pe m banda imediat și o altă modalitate

de construcție a mediatoarei unui

segment cu ajutorul compasului

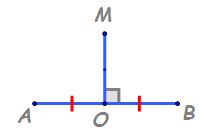
Așadar având un segment AB și punctul

M mijlocul acestui segment m aparține

segmentului AB astfel încât a m

să fie congruent cu MB iar pe m

să fie o perpendiculară pe ab îmi

spune că pe m este mediatoarea

segmentului AB îmi dai și eu proprietate

a mediatoarei unui segment care

va fi scrisă sub formă de teoremă

o teoremă este o propoziție matematică

care exprimă un adevăr ce trebuie

demonstrat orice teoremă are trei

părți ipoteze concluzie și demonstrație

teoremă a cărei ipoteză este concluzia

unei teoreme date și a cărei concluzie

este ipoteza teoremei date se va

numi teoremă reciprocă iar teorema

inițială se va numi teoremă directă

reciproca unei teoreme poate fi

adevărată sau falsă dacă reciproca

este adevărată cele două teoreme

pot fi anunțate între o singură

teoremă unde această proprietate

sub forma unei teoreme directe

și a teoremei reciproce sârma directă

este următoarea dacă un punct aparține

mediatoarei unui segment atunci

el este egal depărtat de extremitățile

segmentului iar teoremă reciprocă

dacă un punct este egal depărtat

de extremitățile unui segment atunci

el aparține mediatoarei segmentului

am arătat că aceste două teoreme

sunt adevărate iar la final le

vom Scrie sub forma unei singure

teoreme începem cu prima teoremă

voi Scrie mai întâi ipoteza și

concluzia avem un segment AB iar

p m este mediatoarea acestuia trebuie

să arătăm că punctul p este egal

depărtat de extremitățile segmentului

pe m este perpendiculară pe ab

M este mijlocul segmentului deci

a m este congruent cu b m trebuie

să arătăm că pe A este congruent

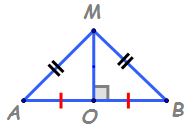
cu p d demonstrație pentru a arăta

că segmentele pe a și pe b sunt

congruente nu am demonstrat că

triunghiurile pe a m și pe b m

sunt congruente observăm că acestea

sunt triunghiuri dreptunghice deoarece

p m este perpendiculară pe ab perpendiculară

pe ab rezultă că măsura unghiului

P m a este egală cu măsura unghiului

pmb și egal cu 90 de grade Deci

avem Două triunghiuri dreptunghice

să vedem Ce elemente congruente

au acestea se știe din ipoteză

că a m este congruent cu b m a

m și b n sunt catetele Două triunghiuri

dreptunghice și a observat că acestea

au o latură comună aceasta este

latura pe m pe m este catetă în

fiecare dintre cele două triunghiuri

am este congruent cu p m fiind

o latură comună din aceste două

relații va rezulta conform cazului

de congruență catetă catetă că

triunghiul p a m este congruent

cu triunghiul p b m ia din congruență

acestor două triunghiuri va rezulta

și congruența segmentelor pe a

și pe b ziceam Arătați că dacă

un punct aparține mediatoarei unui

segment atunci el este egal depărtat

de extremitățile segmentului Să

demonstrăm acum teorema reciprocă

avem un punct P egal depărtat de

extremitățile unui segment având

segmentul ab Se știe că A este

congruent cu pb trebuie să arătăm

că acest punct p aparține mediatoarei

segmentului nu faci o construcție

ajutătoare o duci o perpendiculară

din A pe ab mănâncă acest punct

de intersecție cu m și mai trebui

să arătăm că pe m este mediatoarea

segmentului în ipoteză vom scrie

că pe A este congruent cu p b și

trebuie să arătăm că pe m este

mediatoare asta presupune că pe

m este perpendiculară pe AB și

că M este mijlocul segmentului

AB adică mai trebuie să arătăm

că a m este congruent cu b m observăm

că ipoteza teoreme directe este

concluzia teoreme reciproce și

proteza teoreme reciproce este

concluzia teoreme directe demonstrație

să anunțăm construcția făcută fie

pe m perpendicular pe AB Așadar

prima relație din concluzie rezultat

chiar din construcția pe care a

făcut o mai trebuie doar să arătăm

că a m este congruent cu b m pentru

a arăta că a m este congruent cu

BM încadra aceste două segmente

în cele două triunghiuri dreptunghice

care sau format o să comparăm triunghiurile

pe m și pe b m am demonstrat că

acestea sunt congruente iar din

congruența lor va rezulta și congruența

segmentelor a m și b m Așadar dacă

pe m este perpendiculară pe AB

sau format Două triunghiuri dreptunghice

mai rezultă că măsura unghiului

P m a este egală cu măsura unghiului

pmb și noi mai departe cu 90 de

grade ne mai trebuie doar două

elemente respectiv congruente știm

din ipoteza că pe AE este congruent

cu pb pe a și pe b sunt ipotenuzei

cele două triunghiuri această relație

se știe din ipoteză observăm că

aceste triunghiuri mai au și o

latură comună aceasta este cateta

pe m am este congruent cu PN fiind

o latură comună A rezultat din

cele două relații conform cazului

de congruență ipotenuză catetă

a triunghiul b a m este congruent

cu triunghiul p b m Ia de aici

va rezulta că a m este congruent

cu BM Deci am arătat că pe m este

mediatoarea segmentului aceste

două teoreme pot fi scrise sub

forma unei singure este om cu ajutorul

expresiei dacă și numai dacă un

punct aparține mediatoarei unui

segment Dacă și numai dacă este

egal depărtat de extremitățile

segmentului avem un segment AB

și ne propunem să construim mediatoarea

acestui segment nu folosi compasul

vom desena mai întâi un cerc cu

centrul în punctul A și o rază

mai mare decât jumătate din lungimea

segmentului AB apoi construim un

alt cerc cu centrul în punctul

b și având aceeași rază cu primul

cerc observăm că cele două cercuri

se intersectează în două puncte

vom Uni cele două puncte de intersecție

erau suficient și dacă desenam

doar două arce de cerc având aceeași

rază am construit Așadar mediatoarea

segmentului AB folosind proprietatea

din teorema pe care tocmai am demonstrat

o putem să notăm acest segment

cu el și îmi spune că e pe este

mediatoarea segmentului AB în continuare

o să discutăm despre mediatoarele

laturilor unui triunghi În triunghiul

ABC AB Construiți mediatoarele

laturilor observăm că aceste mediatoare

se intersectează în punct pe care

îl am notat cu o având în vedere

că O aparține mediatoarei segmentului

ac o este egal depărtat de extremitățile

segmentului ac adică distanța de

la o la punctul a va fi egală cu

distanța de la o la punctul c punctul

o și în situat și pe mediatoarea

segmentului b c l va fi egal depărtat

de extremitățile segmentului BC

adică segmentul OB va fi egal cu

segmentul o c iar punctul O fie

în situat și pe mediatoarea segmentului

AB il va fi egal depărtat și de

extremitățile segmentului AB alte

cuvinte constatăm că segmentele

a o o b și o c sunt segmente congruente

înseamnă că putem să construim

un cerc cu centrul în punctul o

și având ca rază unul din aceste

segmente voi construi Așadar un

cerc cu centrul în o observăm că

acesta trece prin vârfurile triunghiului

ABC din acest motiv iar se va numi

Cercul circumscris triunghiului

ABC în cazul în care triunghiul

ABC este ascuțitunghic punctul

o adică centrul cercului circumscris

triunghiului va fi situat în interiorul

triunghiului a b c dacă triunghiul

abc este dreptunghic observăm că

punctul o va fi situat pe latura

AC adică pe ipotenuza triunghiului

dreptunghic punctul o va fi situat

chiar în mijlocul ipotenuzei Dacă

triunghiul ABC este obtuzunghic

observăm că punctul o va fi situat

în exteriorul acestui triunghi

rețineți că intersecția mediatoarelor

laturilor unui triunghi este centrul

cercului circumscris triunghiului