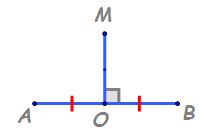
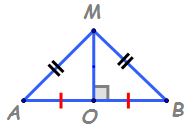
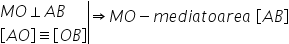Mediatoarea unui segment. Aplicatie.
Tag-uri
Partajeaza in Google Classroom
Transcript
În triunghiul ascuțitunghic ABC
consideră un punct m aparținând
laturii b c ducem MD perpendiculară
pe AB Fie P Un punct situat pe
dreapta m d astfel încât PD congruent
cu dm ducem m e perpendicular pe
AC Fie P Un punct situat astfel
încât m n congruent cu n q Arătați
că triunghiul a p q este isoscel
construim un triunghi ascuțitunghic
ABC și fixă un punct M pe latura
b c ducem din m o perpendiculară
pe AB aceasta este MD Fie P Un
punct situat pe dreapta m d astfel
încât punctul d să fie în interiorul
segmentului p m și p d să fie congruent
cu dm cu alte cuvinte prelungim
segmentul MD un alt segment d p
congruent cu acesta din m mai ducem
o perpendiculară pe latura AC aceasta
este m i și prelungim segmentul
n e un alt segment aq congruent
cu acesta punctul E trebuie să
fie situat în interiorul segmentului
mq trebuie să arătăm că triunghiul
a p q este isoscel să scrie mai
întâi ipoteza și concluzia avem
un triunghi abc oarecare și un
punct M care aparține laturii BC
ducem MD perpendiculară pe ab nu
voi mai scriu toate relațiile de
apartenență prelungim segmentul
MD un alt segment congruent cu
acesta de pe apoi ducem m e perpendiculară
pe AC trenul Gym segmentul m n
un alt segment a q astfel încât
aceste două segmente să fie congruente
trebuie să demonstrăm că triunghiul
a p q este isoscel un triunghi
este isoscel dacă are două laturi
congruente conform figurii putem
intui că aceste două laturi ar
fi ape și aq Așadar în concluzie
vom scrie a p congruent cu aq demonstrație
Se știe că p d este congruent cu
dm înseamnă că punctul D este mijlocul
segmentului BM apoi m d este perpendiculară
pe AB înseamnă că AD este mediatoarea
segmentului pe m punctul A fiind
situat pe mediatoarea segmentului
pe M L va fi egal depărtat de extremitățile
acestui segment conform teoremei
amintite mai devreme Așadar parez
multa că AB este congruent cu a
m să scriem cele spuse până acum
știind că m d este perpendiculară
pe a d din ipoteză PD este congruent
cu dm Acest lucru se știe tot din
ipoteza în aceste două relații
rezultă că a d este mediatoarea
segmentului pe m înseamnă că punctul
A este egal depărtat de punctele
b și m cu alte cuvinte a p este
congruent cu a m conform teoremei
amintite mai devreme mâna ta această
relație cu unu pentru că o va folosi
mai târziu punctul n este mijlocul
segmentului mq pentru că se știe
că m este congruent cu aq apoi
mai știind că m este perpendiculară
pe a ce Așadar observăm că a e
este mediatoarea segmentului mq
punctul A fiind situat pe mediatoarea
segmentului el va fi egal depărtat
de extremitățile segmentului mq
Așadar distanța de la punctul A
la punctul M va fi egală cu distanța
de la punctul A la punctul q deci
a m a fie congruent cu aq să scriem
și aceste date îmi este perpendiculară
pe AC Acest lucru se știe din ipoteză
segmentul m n este congruent cu
segmentul eq Acest lucru se știe
tot din ipoteză din aceste două
relații va rezulta că a e este
mediatoarea segmentului mq înseamnă
că punctul a este egal depărtat
de punctele m și q mai exact segmentul
a m va fi congruent cu segmentul
aq acest lucru sa demonstrat între
ma anunțat anterior Buna Taci asta
relație cu doi observăm că AB este
congruent cu a m și a m este congruent
cu aq înseamnă că putem spune conform
acestor două relații aperi este
congruent cu aq să ne uităm și
pe figura AB este congruent cu
aq așadar am demonstrat că triunghiul
apq este un triunghi isoscel cum
scrie la final din relația 1 și
2 ma rezultat că ape este congruent
cu aq Așadar triunghiul a p q este
un triunghi isoscel
Mediatoarea unui segmentAscunde teorie X
Navigare în lectii
Cumpara abonament
