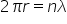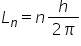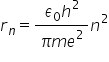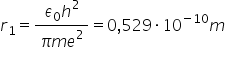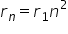Modelul Bohr: condiţia de cuantificare, cuantificarea razelor.
Tag-uri
Partajeaza in Google Classroom

Transcript
în cele cinci ale lecției de fizică
atomică dezvoltăm modelul Atomic
bohr întro prima lecție urmând
ca lecția următoare să termine
dezvoltarea modelul Atomic al lui
bohr amintesc în lecția precedentă
am stabilit cele două postulate
ale lui bohr ce stau la baza acestui
model noi urmând acum să le aplicăm
pentru a dezvolta acest model deci
la bază formalismului matematic
al modelului vor stă așa numita
condiție de cuantificare care rezultă
din două idei fundamentale prima
dintre ele este primul postulat
Bor vă reamintesc simplificat un
pic spuse primul postulat Bor spune
că electroni se află în atom în
jurul nucleului pe orbite staționare
ceea ce după cum am spus încalcă
electromagnetismul clasic dând
acest caracter pur cuantic al modelului
lui bohr Deci esențial în primul
postulat este că electroni se află
pe orbite staționare al doilea
a doua idee fundamentală de la
care vor a pornit este că electronii
fiind particule sau sisteme fizice
de tip cu antic vor respecta dualismul
unda corpuscul tipic fizicii cuantice
introdus de către De Bruyne în
ipoteza sa asta înseamnă că electronii
vor avea electroni care sunt corpusculi
adică particule microscopice vor
avea o undă asociată în aceste
două idei în aceste două enunțuri
se află în cuvinte scrisă Punctul
de plecare pentru o condiția de
cont ificare Deci ar trebui ca
a dumneavoastră Vă puteți uita
la aceste două enunțuri și să vedeți
cuvintele cheie de la care puteți
stabili o condiție de cuantificare
Deci poate că ar fi o idee bună
să puneți pauză video lui pentru
un minut și să vă gândiți un pic
de unde ar putea sunt Anca și cuvinte
cheie din cele două propoziții
care le vedeți o condiții de cuantificare
Adică o condiție prin care două
mărimi ale electronului Sunt legate
prin drumurile întreg un număr
întreg o mărime a este egală cu
număr întreg înmulțită cu o mărime
b unde ar putea să rezulte de aici
Ok în continuare Haideți să stabilim
Care sunt cele două cuvinte cheie
o să le subliniez primul cuvânt
cheie este cuvântul staționar și
cel de al doilea cuvânt cheie este
cel de undă asociată electronul
deoarece aceasta implică că un
duh asociat electroni trebuie să
fie un de staționar și deja ar
trebui să vă gândiți imediat la
studiul pe care îl am făcut în
cazul undelor mecanice Spre exemplu
studiul interferenței staționare
care ducea la unde mecanice staționare
întorc werden coarda unei chitări
de exemplu obținem unde staționare
dacă avem o anumită condiție îndeplinită
acea condiție Era ca lungimea corzii
în cazul acela al orbitei electronului
în cazul nostru să fie un multiplu
al lungimii de undă Deci în cazul
nostru condiția de cuantificare
adică ecuația de baza de la care
pornește toate pornesc toate ecuațiile
modelului Bor este aceea că lungimea
orbitei trebuie să fie un multiplu
întreg n Aici este un număr întreg
1 2 3 și așa mai departe de lungimea
de undă a unde asociat electron
vom vedea imediat Ce rezultă din
această ecuație dar aș sublinia
încă o dată că ca întotdeauna în
fizică esența nu stă în formule
ce este esența stă în cuvinte mulți
elevi se străduie foarte mult să
rețină și să înțeleagă legăturile
dintre formule dar nu neapărat
se strădui să înțeleagă care sunt
ideile din spatele formulelor matematice
întotdeauna ideile sunt mai importante
pentru că ele conțin proprietățile
de bază fundamentale ale teoriei
respectiv bineînțeles și formula
vânt importanța lor pentru că ne
permit descrierea sistemului proprietăților
revenind în cazul acesta faptul
că în faptul că Bor a stabilit
două lucruri și anume că orbitele
sunt staționare și că e folosit
dualismul unda corpuscul deoarece
electronii sunt sisteme cuantice
modelul lui bohr este un model
de tip cu anti după cum am stabilit
în lecția trecută aceste două idei
împreună de fapt în tot pentru
că imediat rezulta ceastă ecuație
și vom vedea în două lecții Cum
anume dezvoltăm o serie întreagă
de ecuații plecând numai de aici
Bun deci să continuăm Păi după
cum știm ipoteza De Bruyne spune
exact cât este lungimea de undă
a asociată unei particule și anume
kalenda este h Constanța lui planck
împărțit la P deci putem scrie
mai exact această ecuație ca circumferința
orbitei electronice adică 2 Petre
este n un număr întreg înmulțit
cu h împărțit la pe iarăși subliniez
această ecuație este ecuația tipică
de pentru fizica cuantică datorită
apariției acestui an fiind un multiplu
întreg scrind explicit valoarea
nu deocamdată nu skin explici valoarea
lui pi de aici rezultă imediat
condiția de cuantificare deci de
aici rezultă că produsul dintre
raza electronului pe orbită a lui
staționară și impulsului trebuie
să fie un multiplu întreg de așa
numita constantă plan Credis să
deci habar este Oetker simplu notație
hba1 tatie pentru Constanța lui
planck împărțită la 2 pi și o introducem
pentru că de foarte multe ori Constanța
lui planck apare în ecuații împărțită
la 2:00 pic și pentru A simplifica
ecuațiile notăm și împărțit la
2 pi h q h par Deci obținem că
airport trebuie să fiu multiplu
întreg de o constantă aceasta este
în mod Evident o ecuație de tip
cu antic în stânga avem multiplu
întreg de o constantă și intrat
avem produsul raza ori Impuls aceasta
este ecuația de baza de la care
pornește modelul lui bohr se numește
condiția de cuantificare ce spune
ea este foarte simplu de reprezentat
vizuală conținutul fizic al acestei
ecuații spune că dacă un electroni
se află în rotație în jurul nucleului
necesita este electronul nostru
atunci orbita lui vorbit aplecare
se deplasează de scrie o traiectorie
staționară Deci stabilă dacă un
da asociatului este un multiplu
de Lambda Asta înseamnă reprezentând
vizualul ca această undă trebuie
să se termine așa să se termine
complet Deci dacă undă asociată
electronului pe această orbită
este în acest fel atunci această
undă este staționară este stabilă
și electronul va sta pe un tip
timp indefinit ce se întâmplă cu
altă orbită de să zicem că luăm
alta orbită la altă poziție a al
aceluiași electron și bineînțeles
modificând R raza lui atunci iar
lungimea acestei orbite nu va mai
fi multiplu de la ce se va întâmpla
Evident este că ea se va termina
ceva de genul acesta undă asociată
nu se va mai închide în în această
situație electronul se afla pe
o pe o orbită instabilă și Deci
nu această stare atomului nu va
putea exista în concluzie condiția
de cuantificare ne spune care sunt
orbitele electronilor care sunt
staționare stabile și deci în care
atomul poate sta un timp indefinit
celelalte orbite sunt cele care
dispare imediat pentru că nu îndeplinesc
această condiție de staționar itate
Buna continuând putem deduce prima
lege de cuantificare și cea mai
ușor cea mai imediată ecuații din
condiția de canti fie Care este
cea pentru momentul cinetic el
ne particule momentul cinetic al
unei particule sau unui corp și
în mecanica clasică ținut este
un factor se notează cu m și este
produsul vectorial dintre vectorul
poziție și vectorul Impuls în cazul
particular în care el și pe sunt
perpendiculare care este cazul
nostru Deci r provine din nucleu
acesta este vectorul r vectorul
p este dar lungul vectorului viteză
care este tangent la traiectorie
Deci modulul lui El este erori
pandel acesta este exact condiționată
de cuantificare Deci pentru un
fel condiția de cuantificare spune
de prima lege de cuantificare și
anume că moment magnitudinea sau
modulul momentului cinetic al unui
electron pe orbită staționar este
un multiplu de Haș bar Deci e cuantificat
în concluzie cuantificarea orbitelor
electronilor atomice se bazează
pe două idei fundamentale staționar
itatea orbitelor deci a stărilor
atomice în care ori vorbit electronilor
se află în acele poziții și pe
caracterul dual unda corpuscul
ale electronilor care înseamnă
că Considerăm electronii ca fiind
particule descrise de fizica cuantică
și aici am de dus condiția de cuantificare
și prima legi de cuantificare cea
pentru momentul cinetic orbita
următoarea lege folosește condiția
de echilibru aceste un orbital
electron ore sunt staționare dar
ca să fie și un echilibru trebuie
după cum am spus și după cum rezultă
din modelul lui Russell Ford calatorului
ridica forța de atracție electrostatică
să fie egală cu forța centrifugă
deci punem această condiție suplimentară
ca forța elastică forța scuzați
electrostatică să fie egală cu
forța centrifugă din mecanica clasică
putem scrie formula forței centrifugale
este mp pe trapez și din electrostatică
știm formula forței electrostatice
Care este a pătrat împărțit la
4 pe epsilon 0r pătrat de ce e
pătrat pentru că cele două sarcini
sunt ale electronului este bineînțeles
și ale atomului am considerat tu
tot e pentru că deocamdată dezvoltăm
formalismul pentru atomul de hidrogen
care are Zet egal cu unu în curând
sau în câteva minute voi comenta
și asupra cazului Zet mai mare
decât unul adică a tuturor celorlalți
atomi decât Deci deocamdată considerăm
un atom de hidrogen care are un
nucleu cu Z egal cu plus 1 Deci
ecuația atunci devine aceasta care
poate fi scris în felul următor
m pătrat de pătrat R pătrat este
egal cu m e pătrat orar împărțit
la 4 pe epsilon zero am dus R pătrat
în partea stângă în partea dreaptă
și amorțit cu m aplicăm condiția
de cont ificare Care este r p egal
cu n H bar adică rmw egal cu n
H par rezultă că făcând substituții
le pentru RMZ Deci această parte
stângă va fi m pătrat habar pătrat
adică ceea ce vedem aici egal cu
m a pătrat 4 piețelor 0 simplificând
obținem legea de cuantificare a
razelor orbitelor de chiar va fi
egal cu un i m pătrat înmulțit
cu o constantă pe care o notăm
cu l 1 și care este egală cu următorul
are următoarea ecuație de ce 1
din această ecuație va fi egal
cu epsilon 0h pătrat împărțit la
tipa la rămâne un pic un pic se
simplifică Fie m e pătrat și care
toate aceste mărimi sunt constante
înlocuind Iuli obținem această
valoare Care este raza Prime vorbit
ibor Deci razele orbitelor electronilor
sunt un număr întreg la pătrat
înmulțit cu aer 1 care este raza
Prime vorbiti si cea mai apropiată
de nucleu care se numește și prima
orbită Borșa are această valoare
celelalte vor fi Deci 2 la pătrat
R1 adică patru Air 1 3 la pătrat
Adică noi unul și așa mai departe
acesta este lege de canti fie care
a razelor orbitelor electronilor
Aici am scris ceea ce tocmai am
discutat acum în concluzie acestei
ecuații pot fi folosite doar pentru
atomul de hidrogen deoarece în
expresia forței electrostatice
am ținut cont doar de interacția
electron nucleu Deci ce vreau să
spun vreau să spun următorul lucru
când scriem ecuația forța electrostatică
acționează asupra electronului
este egal cu forța centrifugală
decembrie pătrat pe el am scris
explicit această ecuație ca fiind
e pătrat împărțit la 4 pe salon
0r pătrat în principiu Am putea
spune că dacă nucleul are sarcina
z am adăuga un set deoarece sarcina
nucleară fissette sarcina electronului
este Deci produsul sarcinilor este
pătratul și acest lucru nu ar fi
corect pentru că ține cont doar
de interacție electrostatică dintre
electroni și nucleu dar atomul
nostru dacă z este mai mare decât
1 atunci trebuie să aibă mai mulți
electroni De ce există un număr
egal cu Z de electroni și există
o forță de respingere dintre electroni
Deci această formulă a forței electrostatice
ce acționează asupra unui electron
este incompletă ar trebui să adăugăm
și Forțele de interacțiune crosta
Teach dinte electroni dintre ceilalți
electroni Deci atomic cu Z mai
mare decât nu au mai mulți electroni
și atunci trebuie să includem în
formula forță electrostatice și
multitudinea de interacției lectron
electron și Deci formula noastră
care a conținut numai acest termen
e valabilă doar pentru atomul de
hidrogen Ea este de asemeni valabilă
și pentru așa numiții atomi hidrogen
care de fapt sunt Ioni din care
sau eliminat toți electronii mai
puțin unul Deci dacă luăm orice
atom și eliminăm toți electronii
mai puțin nu atunci bineînțeles
ne întoarcem la situația în care
avem doar un nucleu și un electron
și atunci putem pune în în formula
forței electrostatice un z de substituie
pătrat cu z a pătrat și atunci
ecuațiile de cuantificare Spre
exemplu de cuantificare a razei
electronul rămân corect în particular
ce se modifică în ecuația de care
a razei substituie pătrat cu ZTE
pătrat și Deci 1 pentru un atom
hidrogenoid va deveni Air 1 împărțit
la 10 ceea ce are sens bineînțeles
pentru că dacă știm sarcina nucleului
de la plus 110 egal cu noua Hydro
genului La un anumit fornite valoare
Zet atunci rectorul nu va fi atras
mai puternic de către nucleu Dar
ce Acesta are sarcina mai mare
și Deci raza sau orbita aflat în
echilibru va fi mai aproape de
nu prea