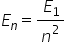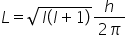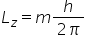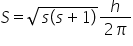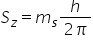Modelul păturilor pentru atomi cu Z>1. Numerele cuantice (n,l,m,mS).

în cea de a noua lecții de fizică

atomică vom discuta despre atomul

cu mai mulți electroni adică cu

10 mai mare decât 1 în lecțiile

trecute am discutat despre modelul

bohr și despre faptul că acesta

Explică foarte bine proprietățile

atomului de hidrogen precum energia

de ionizare sau seriile spectrale

să vedem acum cum stă situația

în cazul atomilor cu mai mulți

electroni în particular vom discuta

despre așa numit un model al pădurilor

electronice care a fost dezvoltat

de către veri savanți dar în principal

de către șoricel și pleacă de la

limitările modelul bohr după cum

am discutat deja când am dezvoltat

modelul bohr limit principala limitare

vine din tratarea simplistă a interacțiunilor

din atom mai exact se folosește

doar o forță electrostatica nucleo

electron dacă va aminti aveam așa

numita lege de sau condiție de

echilibru al orbitei electronilor

care spunea că forța centrifugă

este egală cu forța electrostatica

de interacție dintre nucleu și

electron și această forță electrostatica

era scrisă ca minus a pătrat împărțit

la 4 pini epsilon 0 aer unde R

era distanța dintre nucleu și orbita

electronului și ca o are care extensie

puteam folosi aceasta acest model

al lui bohr și pentru așa numiții

atunci hidrogenoizi adică atomi

cu 10 mai mare decât 1 dar cu un

singur electron acest model a lui

Bor funcționat foarte bine pentru

că aveam un singura interacție

în atom și anume cea dintre electroni

și nucleu în cazul atomilor cu

un sat mai mare decât unul nu mai

e suficient să avem numai această

forță de interacție ci bineînțeles

trebuie să adăugăm adăugăm și multitudinea

de interacției electrostatice dintre

electronii atomului mai exact trebuie

să avem un sumă de felul a pătrat

împărțit la 4 pi epsilon 0 în scuzați

Forța este cu er la pătrat Deci

Neptun 0 r e j la pătrat unde R

E J este distanța dintre electronul

e și electronul j mă acesta este

motivul și pentru care această

forță este pozitivă pentru că doi

electroni au sarcină în amândouă

lecturi nu au sarcina negativă

Deci produsul va fi pozitiv în

concluzie oprima extensii ar trebui

ar trebui să fie următoarea să

includem o multitudine de forțe

electrostatice de interacțiune

oricare pereche distinctă de electroni

Deci trebuie inclus interactive

Electro Electro mai mult decât

atât o simplificare o altă simplificare

mai puțin importantă dar care are

și impactul ei este faptul că Considerăm

aceste interacției de tip electrostatic

Dar bineînțeles ar trebui să Considerăm

cazul mai general din interactii

electromagnetice adică în care

toate componentele câmpurilor și

magnetice atâta ale nucleului cât

și ale electronilor aflați în mișcare

trebuie luate în considerare Spre

exemplu un atât nucleul cât și

electronii au un câmp magnetic

propriu generează un câmp magnetic

propriu deoarece sunt în mișcare

minți în principală electronilor

avea această proprietate și Deci

vom avea o valoare lui b pentru

a Câmpului magnetic propriu electronilor

de obicei notat Cum eu nu contează

acest lucru Ce contează este că

în scrierea ecuației interacției

dintre electroni Spre exemplu sau

dintre electroni și nucleu vom

avea o componentă pur magnetic

ar trebui să ținem cont de ea și

așa mai departe Deci în concluzie

ar trebui rescrisă în cazul atomilor

cu 10 mai mare decât 1 ar trebui

rest scrisă întreaga componentă

de interacție din atomi și dezvoltat

un nou model care să țină cont

de toate aceste componente această

problemă rezolvată de școală din

gara modelul său și inecuațiile

și ording este o problemă destul

de complicat în orice caz veste

nivelul de cunoștințe din liceu

ia se face la facultate dacă Alegeți

să faceți un fizica sau chimia

deci noi nu vom adresa rezolvarea

cantitativă adică numerică sau

analitică a atomului cu 10 mai

mare decât 1 și nu mai vom sublinia

principalele consecințe consecințe

cere ies din modelarea completă

a unui astfel de atom nici principala

consecință este că după ce include

De ce este interacția și rezolvă

ecuațiile nivelele energetice pe

care le aveam în cazul modelului

Bor Care erau descrise de numărul

cuantic principal bineînțeles de

vite mai complicate se transformă

în așa numitele pături electronice

care sunt descrise de un sat mai

complex de numere cuantice Deci

dacă în modelul bohr vorbeam de

nivele energetice descrise de numărul

cuantic principal și atât timp

cât știam valoarea lui n putem

calcula toate valorile tuturor

parametrilor electronului în principal

Spre exemplu energia electronic

pe un nivel energetic cu numărul

cuantic principal n dar puteam

calculat după cum am văzut și raza

orbitei și viteza pe orbită și

așa mai departe frecvența de rotație

și așa mai departe toate.ro legate

de acest an celelalte mărimi în

parametrii în ecuațiile acestor

parametri erau constant de ciudată

dat an pentru starea în care se

afla sau nivelul pe care se afla

un electrocutat calculator parametrii

același lucru se extinde și în

acest caz numai că în loc de un

număr cuantic avem patru pe care

îi vom explica imediat deci pe

lângă numărul cuantic principal

mai există trei alte numere cuantice

l m și m s care descriu starea

în care se află în electron Deci

în tabelul următor sumar ism acest

m numere cuantice Deci ce vedeți

aici este numele numărului cuantic

apoi mărimea caracteristică sau

mărimea Care este cel mai direct

legată de acel număr cuantic ecuația

în care apare explicit acelui număr

cuantic și valorile pe care le

poate lua acel număr cuantic fiind

un număr cuantic el Ia valori discrete

Deci primul număr cuantic este

numărul cuantic principal de care

am discutat deja în cadrul modelului

Bor care își păstrează aceeași

semnificație Deci numărul cuantic

principal este legat de energia

pături electronici în cazul acesta

El e legat de energie prin această

ecuație bine cunoscută de Ce este

energia stării fundamentale împărțită

la n pătrat și după cum știm n

ia cavalor orice număr întreg pozitiv

n este egal cu 1 2 3 4 și așa mai

departe acum noile numere cuantice

primul număr cuantic nou este așa

numitorul număr cuantic orbital

notat cu l mic El este legată de

momentul cinetic orbital prin relația

următoare valoarea absolută a momentului

cinetic orbital El este radical

din numărul cu anticor Beetle al

înmulțit cu el plus 1 înmulțit

cu HB HT HT la doi pini valorile

discrete ale acestui moment cinetico

orbita sunt toate valorile întregi

de la 0 până la el minus unu deci

el Ia n valori de la 0 la el minusul

Deci pentru un an dat el va avea

n valori motorul este momentul

magnetic orbital care este legat

de proiecția lui el pe o anumită

exces admis taxa de cuantificat

Deci l z m este legat de el zac

Deci valoarea lui el de a lungul

axei o zi prin această ecuație

iar numărul magnetic orbital m

este și el un număr întreg care

ia toate valorile de la minus la

plus Deci pentru un l dat Spre

exemplu pentru l egal cu doi avem

toate valorile de la minus 2 la

plus 2 Care sunt cinci valori 2

L plus 1 există un număr cuantic

de spin esti Dar nu la nota cu

roșu aici pentru că se întâmplă

ca acest număr cuantic de spin

să iau o singură valoare și atunci

el are practic o semnificație redusă

în noi nu putem obține în consecință

mai multe stări datorită acestui

număr cont ID Simt pentru că din

nou ilario singura valoare următorul

și ultimul număr important este

numărul Magnetic de spin MS Care

este proiecția pe axa a z a momentului

cinetic de spin și care ia două

valori de ce ia valoarea minusul

1 pe 2 și plus 1 pe 2 din acest

motiv și anume faptul că Ilia mai

mult de o valoare devină un număr

cuantic importantă pentru că duce

la multiplicarea cu 2-a număr a

numărului de stări posibile deci

sunt mari zând introducând interacțiunea

interacțiunea completă din atom

cu 10 mai mare decât 1 adică ținând

cont de toate aceste interacție

situația bineînțeles devine mai

complexă mai complicată în sensul

că energiile energetice scuzați

nivele energetice descrise de un

singur număr cuantic din modelul

Borg devin pături electronice descrise

de un set de patru numere cuantice

n l m și MN și vom vedea ce implică

aceasta un singur comentariu care

vom vedea imediat că este important

am spus că Gia unei pături electronice

sau mingea unei stări electronice

dacă doriți Este legată numai de

numărul cu anticipat prin această

formulă de fapt această afirmație

în principiu corectă dar în practică

există deviație în sensul că între

adevăr energia unei stări electronice

este dată de această formulă dar

există o mică corecție care depinde

de el deci există o mică componentă

a energiei unei stări a electronului

ce depinde și de el și aceasta

va avea implicații în