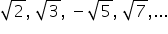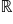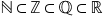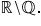Mulțimea numerelor reale

în această lecție o să vedem ce

este mulțimea numerelor reale dar

mai întâi să ne reamintim puțin

mulțimile de numere învățate Până

acum în clasele mai mici au învățat

mulțimea numerelor naturale aceasta

conține numerele 0 1 2 3 și așa

mai departe Ea este formată doar

din numere pozitive apoi a fost

introdusă în mulțimea numerelor

întregi care se notează cu Z iar

conține atât numere naturale cât

și opusele acestora adică numere

de formă a minus 3 minus 2 minus

1 0 1 2 3 și așa mai departe apoi

am învățat fracțiile și am văzut

că acestea reprezintă mulțimea

numerelor raționale care se notat

cu q Așadar mulțimea numerelor

raționale este formată din fracții

de formă a supra b unde a și b

sunt numere întregi iar b este

diferit de 0 mulțimea numerelor

raționale conține și fracții zecimale

finite pentru că am văzut că Acestea

se pot scrie sub forma unei fracții

ordinare de exemplu fracția 5 se

poate scrie sub formă de fracție

ordinară 562 supra 100 care la

rândul ei se mai poate simplifica

Așadar 5 este un număr rațional

mulțimea Q mai conține și fracții

zecimale infinite dar periodice

am văzut cu o fracție zecimală

periodică de forma 1 se poate transforma

în fracție ordinară un întreg trei

supra 9 după ce introducem întregii

în fracție obținem 1 ori 9 plus

3 adică 12 supra 9 Așadar Aceasta

este o fracție ordinară Deci este

număr rațional mai rămâne o singură

categorie de fracții și anume fractii

zecimale infinite și neperiodice

acestea nu pot fi scrise sub forma

unei fracții ordinare Deci nu vor

fi numere raționale nefiind numere

raționale se vor numi numere iraționale

Bogdan continuare definiția numerelor

iraționale după cum spuneam un

număr irațional este o fracție

zecimală infinită și ne periodică

aceste numere iraționale împreună

cu mulțimea numerelor raționale

formează o nouă mulțime care se

notează cu r și se numește în mulțimea

numerelor reale pentru a înțelege

mai bine relația dintre aceste

mulțimi putem privi această diagramă

mulțimea numerelor naturale este

reprezentată prin cercul galben

din mijloc aceasta se notează cu

N urmează apoi mulțimea numerelor

întregi apoi mulțimea numerelor

raționale și cea mai mare dintre

toate aceste mulțimi este mulțimea

numerelor reale mulțimea numerelor

reale minus mulțimea numerelor

raționale este formată din mulțimea

numerelor iraționale Deci partea

aceasta hașurată cu verde reprezintă

numerele iraționale adică acele

numere pe care mulțimea numerelor

reale le are în plus față de mulțimea

numerelor raționale are loc această

incluziune n este inclus în z inclus

în q și inclusă în r o să vedem

în continuare câteva exemple de

numere iraționale momak strige

în continuare rădăcina pătrată

a numărului 2 Folosind algoritmul

pe care la învățat în lecțiile

trecute cel mai mic număr care

ridica la pătrat ne dă un număr

mai mic sau egal decât 2 este 1

1 ridicat la a doua este 1 Efectuați

scăderea punem virgulă și adăugăm

două cifre de 0 această virgulă

se adaugă și la rezultat coborâm

cele două cifre de 0 lângă 1 dublăm

această cifră și obținem 2 merităm

la numărul 100 și norum ultima

Star cifră mă face 10 împărțit

la 2 care este 5 iar numărul 25

se înmulțește din nou cu cinci

și obținem 125 pentru că 125 este

mai mare decât 100 înseamnă că

cifra 5 nu este corectă și vom

încerca cu o cifră mai mică mă

face 24 ori 4 Care este egal cu

96 96 se trece sub 100 și afectuos

că cifra 4 obținută aici se așează

la rezultat mai adăugăm o grupă

de două cifre de 0 care se coboară

lângă patru dublăm acest număr

fără să ținem cont de virgulă 14

ori 2 este 28 notăm la numărul

400 și ignorăm ultima cifră 40

împărțit la 28 este 1 iar numărul

281 se înmulțește cu 1 și obținem

281 trecem acest număr sub 400

și efectuăm scăderea obținem 119

iar cifra 1 se trece la rezultat

mai adăugăm 20 ori dublăm numărul

obținut aici fără a ține cont de

virgulă 141 ori 2 este 282 ne uităm

la numărul 11.900 ignorăm ultima

sa cifră și efectuăm împărțirea

1190 împărțit la 282 vom obține

câtul 4 numărul 2824 se înmulțește

cu patru după ce faceți alăturat

înmulțirea vom obține rezultatul

11.200 96 acest număr se trece

sub 11.900 insektum scăderea obținem

640 este 4 se trece la rezultat

după cum Observați acest algoritmi

nu se va termina niciodată pentru

că aici nu vom obține niciodată

restul zero Așadar numărul acesta

va avea o infinitate de zecimale

și în acest caz nu îmi spune că

radical din 2 este un număr irațional

alte exemple de numere iraționale

sunt radical din 3 radical din

5 putem Extragerea de care din

aceste numere folosind același

al gurii și obținem o infinitate

de zecimale un alt exemplu este

radical din 7 minus radical din

6 și așa mai departe în general

numerele iraționale sunt acei radicali

din numere care nu sunt pătrate

perfecte pentru că numerele iraționale

nu se pot scrie explicit și cu

precizie se preferă a fi lăsate

sub formă de radical sau se vor

aproxima cu cel mai apropiat număr

rațional prin rotunjire o să facem

un continuare un exercițiu Se dă

mulțimea a formată din următoarele

numere a minus 5 radical din 3

3 supra 7 radical din 9 supra 16

4 minus 10 supra 5 Calculați la

punctul a se cere să calculăm a

intersectat cu n ne interesează

să vedem Ce elemente comune au

mulțimile A și n mai exact trebuie

să vedem care sunt numerele naturale

din mulțimea a minus 5 este negativ

Deci nu va fi număr natural radical

din 3 este irațional Așadar nu

este număr natural avem apoi fracția

3 supra 7 pentru că trei nu se

împarte exact la 7 această fracție

nu este număr natural nici 9 supra

16 Nu este natural mai mult avem

și radical aici numărul 4 în formă

Care este scris Am putea spune

că nu este număr natural Haide

să transformăm această fracție

zecimală în fracție ordinară patru

virgulă noua în perioadă se scrie

4 întregi 9 supra 9 egal putem

introduce întregii în fracție 4

ori 9 plus 9 supra 9 patru ori

9 este 36 plus 9 45 supra 9 care

va fi egal cu 5 iar 5 este un număr

natural Așadar numărul 4 în perioadă

este număr natural minus 10 supra

5 fiind negativ nu va fi număr

natural închidem acolada punctul

B ne interesează a intersectat

cu Z Adică trebuie să găsim numerele

întregi din mulțimea a mulțimea

numerelor întregi este formată

din ținea numerelor naturale și

opusele acestora Așadar minus 5

va fi număr întreg radical din

3 nu este număr întreg 3 supra

7 este o fracție ordinară iar pentru

că trei nu se împarte exact la

7 Nu va fi număr întreg nici noul

supra 16 Nu este întreg 4 virgulă

perioadă nu am văzut că este număr

natural așa dar va fi și număr

întreg la numărul minus 10 supra

5 dacă facem împărțirea este egal

cu minus 2 și minus 2 este număr

întreg Așadar vei scrie și minus

10 supra 5 în a intersectat cu

z urmează la punctul C să determinăm

elementele mulțimii A minus z ne

interesează acele numere care sunt

în ei dar nu sunt numere întregi

acestea sunt radical din 3 am văzut

că radical din 3 este irațional

de j este număr real 3 supra 7

este număr rațional dar nu este

întreg radical din 9 supra 16 4

virgulă perioadă 9 este natural

iar minus 10 supra 5 este număr

întreg așa dar acestea trei vor

fi elementele mulțimii A minus

z apoi la A minus Q trebuie să

vedem Ce elemente sunt în mulțimea

A dar nu sunt raționale mai exact

vom Scrie numerele iraționale am

văzut în exemplele de mai devreme

ca radical din 3 este număr irațional

Haideți să vedem celălalt radical

radical din 9 supra 16 dacă este

număr irațional dar de cal din

9 supra 16 se poate scrie radical

din 3 supra 4 totul la puterea

a doua egal mai departe cu 3 supra

4 iar 3 supra 4 fiind o fracție

ordinară va fi și număr rațional

înseamnă că nu este număr irațional

de singurul număr irațional din

mulțimea A este radical din 3