Mulțimi finite. Multimi infinite
Tag-uri
Partajeaza in Google Classroom

Transcript
să vedem acum Ce este aceea o mulțime
finită și Ce înseamnă mulțime infinită
și pentru aceasta vom enumera elementele
unor mulțimi și începem cu această
mulțime Vrem să vedem să descriem
mulțimea a girafelor care locuiesc
pe soare Păi noi știm că pe soare
temperatura este foarte foarte
ridicată asta înseamnă că nu este
permis să viața așa cum o știm
noi carevasăzică nu e posibil ca
o girafă să înlocuiască pe soare
Deci această mulțime x cu proprietatea
că x este girafă și trăiește pe
soare Este o mulțime care nu are
niciun element o mulțime care nu
are elemente se numește mulțime
Haideți să mă pe maici mulțime
vidă și folosim această notație
avem un 0 tăiat cu o bară și anul
tot aici mulțimea vidă Deci mulțimea
care nu are niciun element sigur
există mai multe mulțimi vide de
exemplu un mulțimea m bufnițelor
care folosesc calculatorul sau
cum a notat aici mulțimea formată
din elementele x cu proprietatea
că x este Bufniță și lucrează pe
tabletă și aceasta este tot o mulțime
vidă deci putem să notăm același
sens pentru că toate mulțimile
în vid sunt egale între ele Le
reprezintă una și aceeași mulțime
de ce aici avem de fapt egalitate
reține că Mulțimea vidă este mulțimea
care nu are niciun element să descriem
o altă mulțime și avem mulțimea
formată din elementele x cu proprietatea
că x este număr natural vede să
enumerăm elementele care este cel
mai mic număr natural 0 Deci avem
0 urmează 1 2 3 și așa mai departe
Considerăm că am scris până la
2015 ori Maya 2016 2017 sau să
terminăm vreodată descrise aceste
numere nu Din ce cauză pentru că
șirul numerelor naturale este un
șir fără sfârșit orice număr natural
am alege de exemplu 119 numere
aici să apară un număr mai mare
25 orice număr natural am alege
putem să găsim un număr mai mare
decât el de exemplu scrie Maricela
și cifre ca până aici și în loc
de 25 punem la final 26 De ce a
murit cu o unitate acest număr
acest lucru putem să îl facem la
nesfârșit Deci șirul numerelor
naturale este unul fără sfârșit
asta înseamnă că această mulțime
reprezentat de mulțimea numerelor
naturale este o mulțime infinită
bun Haideți să închidem aici acolo
la dar așa Descrie în faptul că
avem o mulțime infinită să știți
că Mulțimea numerelor naturale
se notează cu n mare Da și la acest
an îngrășăm această linie și avem
aici că mulțimea numerelor naturale
este cea descrisă aici și aceasta
este notația putem să discutăm
și despre mulțimea numerelor naturale
din care îl scoate m pe zero adică
avem această mulțime x cu proprietatea
că x este număr natural diferit
de 0 sau mai putem spune x este
număr natural nenul Deci nenul
înseamnă diferit de 0 această mulțime
este tot o mulțime infinită și
a se notează tot cu n mare cum
am pus aici însă mai trecem o steluță
deasupra lui și citim n stelat
sau n Star este mulțimea numerelor
naturale nu le mulțimile pe care
le am prezentat în lecția anterioară
erau toate mulțimi finite de exemplu
mulțimea formată din elementele
x cu proprietatea că x este județ
din România Haide să notăm această
mulțime de exemplu cu A mare această
mulțime este o mulțime finită Ce
înseamnă mulțime finită mulțimea
finită este o mulțime care are
un număr finit de elemente Păi
numărul județelor din România este
unul finit Deci avem o mulțime
finită când avem asemenea mulțimile
poate interesa și numărul de elemente
al acestor mulțimi și pentru aceasta
folosind notația card și apoi scrie
mă numele mulțimi în cazul nostru
a mare și citim cardinalul mulțimii
A mare cu alte cuvinte Numărul
de elemente din mulțimea respectivă
și aici ai de sănătatea sunt 41
de județe Dacă punem la numărătoare
și municipiul București avem 40
și două puteam să vorbim de cardinalul
unei mulțimi și atunci când avem
mulțimi Infinite de exemplu mulțimea
numerelor naturale sau a numerelor
naturale diferite de 0 și aici
putem să ne dam cardinalul mulțimii
numerelor naturale fiind o mulțime
infinită arătăm acest lucru trecând
aici semnul infinit a și citim
aici infinit Deci nu este un număr
natural la fel și aici cardinalul
mulțimii numerelor naturale diferite
de 0 avem tot o mulțime infinită
Deci trecem ca acest cardinal este
infinit cardinalul mulțimii vide
ce am spus că este mulțimea vidă
este mulțimea care nu are niciun
element sau se spune că are 0 elemente
Deci cardinalul său este egal cu
zero cu alte cuvinte avem mulțimi
finite adică mulțimile care au
un număr finit de elemente mulțimi
infinite și am dat Aceste două
exemple și mai avem și mulțimea
vidă adică mulțimea care nu are
nici un element

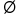
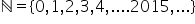
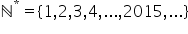 - mulțimea numerelor naturale nenule (infinită)
- mulțimea numerelor naturale nenule (infinită)